2D射影空间中的几何变换
在机器人和刚体运动中,我们关注物体如何从一个位置移动到另一个位置。在计算机视觉中,我们关心相机是如何将三维的世界投影到二维的图像上。 我们的日常生活和工作的方方面面都存在几何变换。从代数的角度看,所谓的几何变换就是一些映射关系,用一个函数将空间中的一个点映射到另外一个点上。 本节中我们讨论射影变换、仿射变换、相似变换、等距变换四种变换。
这些几何变换经常出没在各类工程问题中。在机器人中主要使用等距变换来描述刚体的移动,在计算机图形会研究如何通过射影变换将三维空间中的模型投影到画布上, 在机器视觉中则考虑如何通过多幅或者一幅二维的图像恢复出实际的物理尺寸。
1. 射影变换
若空间 \(\mathbb{P}^2\) 中的三个点 \(\boldsymbol{x}_1, \boldsymbol{x}_2, \boldsymbol{x}_3\) 共线,经过一个变换 \(h\) 后得到的 \(h(\boldsymbol{x}_1), h(\boldsymbol{x}_2), h(\boldsymbol{x}_3)\) 也共线,我们就称变换\(h\)为一个射影映射 projective。 这是从 \(\mathbb{P}^2\) 到其自身的一种可逆映射。
正如其定义所描述的那样,射影映射也被称为保线映射 collineation,有时也称为单应映射 homography。 在 \(\mathbb{P}\) 中,任意一个可逆的\(3 \times 3\)矩阵 \(H\) 都可以构成一个射影变换。假设空间中的点 \(\boldsymbol{x}\) 在直线 \(\boldsymbol{l}\) 上,即\(\boldsymbol{l}^T\boldsymbol{x} = 0\)。带上可逆矩阵 \(H\) 就有\((\boldsymbol{l}^T H^{-1})(H\boldsymbol{x}) = 0\)。 也就是说 \(H\) 将点 \(\boldsymbol{x}\) 映射到了 \(H \boldsymbol{x}\),并且在直线 \(\boldsymbol{l}^T H\) 上。 显然,\(\boldsymbol{l}\) 上的任意三个点\(\boldsymbol{x}_1, \boldsymbol{x}_2, \boldsymbol{x}_3\) 会被 \(H\) 映射到另外一条直线 \(\boldsymbol{l}^T H\) 上。 可以说矩阵 \(H\) 定义了一个从 \(\mathbb{P}^2\) 到 \(\mathbb{P}^2\) 的射影映射,\(H\)是该映射的变换矩阵。可以写成如下的形式: $$ \begin{equation}\label{f1} \begin{bmatrix} x_1' \\ x_2' \\ x_3' \end{bmatrix} = \begin{bmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & h_{33} \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} \end{equation} $$
由于点的齐次坐标\(\boldsymbol{x}\)乘以任意一个非零常数\(k\)表示的都是同一个点,所以上式中\(H\)矩阵乘以任意非零常数\(k\)都成立。 因此虽然\(H\)矩阵有9个元素,但只有8个变量是独立的,即自由度只有8。 所有的射影映射构成一个群 Group,即射影映射的逆还是射影映射,射影映射的组合还是射影映射。
$$ \begin{array}{rcl} \text{作用到点上} & : & \boldsymbol{x}' = H \boldsymbol{x} \\ \text{作用到直线上} & : & \boldsymbol{l}' = H^{-T} \boldsymbol{l} \\ \text{作用到圆锥曲线上} & : & C' = H^{-T} C H^{-1} \\ \text{作用到 dual conic 上} & : & C^{*'} = H C^* H^{T} \end{array} $$射影变换的典型应用就是描述两幅图像之间的映射关系,在机器人定位建图(Simultaneous Localization and Mapping, SLAM)的应用中, 比如经典的 ORB-SLAM2 就会用单应矩阵估计相机之间的相对位姿。
2. 仿射变换(Affine)
如果式(\(\ref{f1}\))中变换矩阵 \(\boldsymbol{H}\) 最后一行向量是 \(\begin{bmatrix} 0 & 0 & 1 \end{bmatrix}\),那么我们就得到了一个仿射变换。可以写成如下的矩阵形式:
$$ \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} a_{11} & a_{12} & t_x \\ a_{21} & a_{22} & t_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} $$ 上式中左上角的 \(2 \times 2\) 的矩阵块 \(A = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix}\) 描述了形状的旋转和变形, 右上角 \(\boldsymbol{t} = \begin{bmatrix} t_x \\ t_y \end{bmatrix}\) 则是一个平移量,可以写成如下的分块矩阵的形式。 其几何含义就是,对目标几何体,先通过 \(A\) 作旋转和变形,再平移 \(\boldsymbol{t}\)。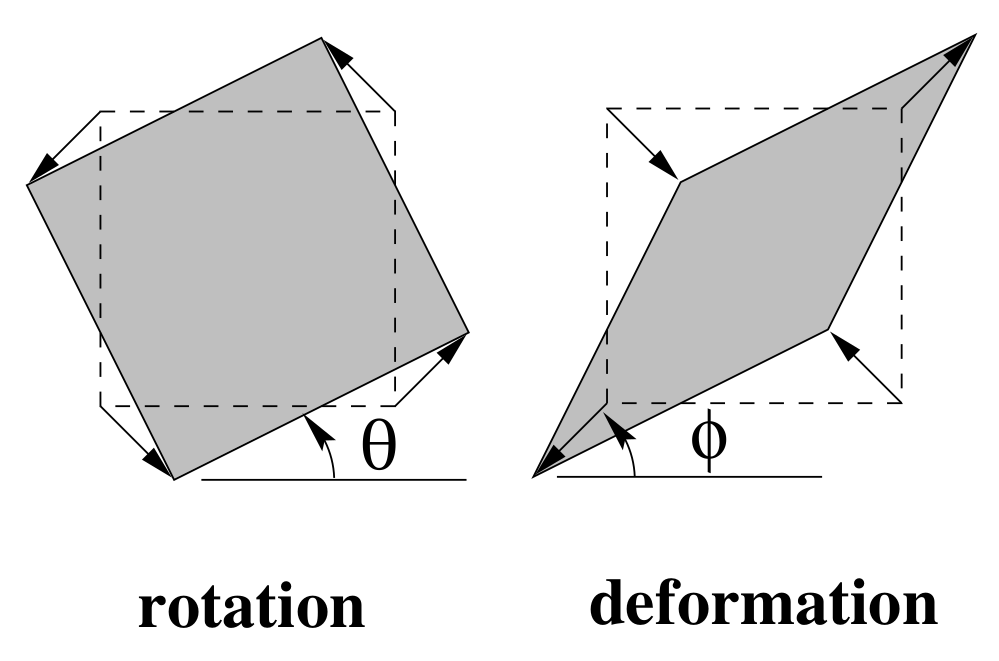 $$
\boldsymbol{x}' = H_{A} \boldsymbol{x} = \begin{bmatrix}
A & \boldsymbol{t} \\ \boldsymbol{0}^T & 1
\end{bmatrix} \boldsymbol{x}
$$
$$
\boldsymbol{x}' = H_{A} \boldsymbol{x} = \begin{bmatrix}
A & \boldsymbol{t} \\ \boldsymbol{0}^T & 1
\end{bmatrix} \boldsymbol{x}
$$
我们将矩阵 \(A\) 称为仿射矩阵(affine matrix),它总是可以分解为如下的形式,如右图所示包含旋转和变形两个部分:
$$ A = \underbrace{R(\theta)}_{rotation} \underbrace{R(-\phi) D R(\phi)}_{deformation} $$其中\(R(\theta)\)和\(R(\phi)\)分别表示旋转了\(\theta\)和\(\phi\)角的旋转矩阵,\(D\)则是一个对角矩阵。 旋转矩阵都是正交矩阵,所以我们可以直接通过 SVD 分解写出 \(A = UDV^T\),其中 \(U = R(\theta)R(-\phi)\),\(V = R(\phi)\)。
矩阵\(A\)的分解从右往左,可以解释为,先对几何体做一次 \(\phi\) 角的旋转,再按照\(D\)的特征值对几何体的 x,y 轴缩放,然后按照 \(-\phi\) 角旋转回来后,附加一个 \(\theta\) 角的旋转。 因为矩阵 \(D\) 对几何体的缩放在x和y轴上并不一定一致,所以仿射变换不能保证形状的不变性。但是平行线关系、平行线段比例、面积的比例这些关系仍然保持不变。
3. 相似变换(Similarity)和等距映射(Isometries)
我们对仿射变换再增加一条约束,要求仿射矩阵 \(A\) 的两个奇异值必须相等,这样就能保证几何体的形状不变。具有如下的矩阵形式:
$$ \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} s \cos \theta & - s \sin \theta & t_x \\ s \sin \theta & s \cos \theta & t_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} $$式中\(s\)表示缩放尺度。写成分块矩阵的形式为:
$$ \boldsymbol{x}' = H_{S} \boldsymbol{x} = \begin{bmatrix} sR & \boldsymbol{t} \\ \boldsymbol{0}^T & 1 \end{bmatrix} \boldsymbol{x} $$如果缩放尺度为 1,就得到了等距映射,即,变换前后点之间的欧氏距离保持不变的映射,可以写作:
$$ \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} \varepsilon \cos \theta & - \sin \theta & t_x \\ \varepsilon \sin \theta & \cos \theta & t_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} $$其中 \(\varepsilon = ±1\)。若\(\varepsilon = 1\),那么上式的变换完全是由旋转和平移构成的,这类变换也被称为欧氏变换 Euclidean transformation。 若\(\varepsilon = -1\),上式除了旋转平移之外还蕴含了翻转的操作。在平面上,欧氏变换可以写成矩阵的形式:
$$ \boldsymbol{x}' = H_{E} \boldsymbol{x} = \begin{bmatrix} R & \boldsymbol{t} \\ \boldsymbol{0}^T & 1 \end{bmatrix} \boldsymbol{x} $$其中\(R\)是一个\(2 \times 2\)的正交矩阵,即\(R^T = R^{-1}\),称为旋转矩阵。\(\boldsymbol{t}\)则是平移向量。我们在研究机器人的问题时, 大多数时候都是在处理刚体的位姿变换。 刚体是空间中一组特殊的质点,这些质点之间的距离保持不变。这正是等距映射的奥义。
4. 完
射影变换是最一般的形式,它有 8 个自由度,只能保证几何体的共线关系。仿射变换是射影变换的一个特例,因为增加了约束,只有 6 个自由度,除了保证共线关系外,还能保证平行关系。 相似变换是一种仿射变换,相比于仿射它增加了约束,要求缩放尺度在各个方向上相同,所以能保证几何体的形状。等距变换则是最特殊的形式,它需要保证各点之间的欧氏距离在变换前后是一致的。
| 符号 | \(H_E\) | \(H_S\) | \(H_A\) | \(H_P\) |
|---|---|---|---|---|
| 变换 | 等距 isometries | 相似 similarity | 仿射 affine | 射影 projective |
| 不变量 | 欧氏距离 | 形状 | 平行关系 | 共线关系 |
| 自由度 | 3Dof | 4Dof | 6Dof | 8Dof |
