Chapter11: 接触与碰撞
Contact and Impact

当两个刚体接触的时候，就会受到一个接触约束, contact constraint，两个刚体不能干涉。用符号 $\phi$ 表示物体之间的距离，如果 $\phi < 0$ 那么这两者就存在交叠的部分(overlap)。所以接触约束可以由不等式 $\phi ≥ 0$ 来表示。这一约束所引入的力也是单侧的(one-sided)，它只能阻止两个刚体相互渗透，但不能阻止他们分离。两个刚体在接触约束下只能相互排斥，不能相互吸引。如果相遇的两个刚体的速度和他们的接触约束不一致，那么就会产生一个导致它们的速度阶跃变化的冲击。我们称这种现象为碰撞, impact。

本章的前四节推导点接触约束下的刚体运动方程。§11.5 节介绍如何求解这些方程。 §11.6 讨论一些几何问题，包括如何通过点接触来表示直线和面接触。 §11.7 推导刚体系统的冲击运动方程，以及两个刚体的碰撞方程。最后，§11.8 将展示另外一种刚体接触和碰撞的动力学建模方法，该方法考虑了接触表面的形变。

11.1 单点接触 Single Point Contact

如图 11.1 所示的刚体系统中有一个刚体 $B$,与一个固定表面在点 $C$ 上接触了。刚体的速度和加速度分别为 $\boldsymbol{v}$ 和 $\boldsymbol{a}$，它还受到主动力 $\boldsymbol{f}$ 和接触力 $\boldsymbol{f}_c$的作用。这里将接触力描述成一个沿着接触法向量 $\boldsymbol{n} \in F^6$ 的力。我们定义法向量 $\boldsymbol{n}$ 垂直于表面向外，这样用一个正数与 $\boldsymbol{n}$ 相乘的物理意义，就是将物体推离表面。我们假设这是一个无摩擦(frictionless)的接触，并且作用在刚体上的力只能是有限的，即在当前接触瞬间不存在脉冲力(no impulses)。在这个系统中存在两个未知数 $\boldsymbol{f}_c, \boldsymbol{a}$，现在我们的问题是想办法找出它们的解。

图 11.1. 一个刚体与一个固定表面在一个点上接触。

令 $C'$ 表示接触瞬间，刚体上与 $C$ 重合的点。固定表面产生一个约束力 $\boldsymbol{f}_c$ 在刚体身上，防止点 $C'$ 穿过表面。因为该接触是无摩擦的，那么该约束力必须沿着接触法向量，因此必定是 $\boldsymbol{n}$ 的数乘。我们引入一个新的标量 $\lambda$，来表示未知的接触力大小，即，

$$ \begin{equation}\label{equa_11.1} \boldsymbol{f}_c = \boldsymbol{n} \lambda \end{equation} $$

因为 $\boldsymbol{f}_c$ 只能排斥刚体，所以 $\lambda$ 必须是正数，即$\lambda ≥ 0$。现在我们引入第二个标量 $\zeta$，来表示接触分离速度(contact separation velocity)。它被定义为点 $C'$ 的线速度在法线方向的分量，表达式为:

$$ \begin{equation}\label{equa_11.2} \zeta = \boldsymbol{n} \cdot \boldsymbol{v} \end{equation} $$

我们可以 $C$ 为原点，法线方向为 $z$ 轴建立一个坐标系来验证 $\zeta$ 的正确性。在普吕克坐标系下 $\boldsymbol{n}$ 将被写成 $\begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 1\end{bmatrix}^T$，因此有 $\boldsymbol{n}\cdot \boldsymbol{v} = v_{C_z}$，这正是点 $C'$ 的线速度的 $z$ 轴分量。

在接触的瞬间有 $\zeta = 0$。这意味着给定向量 $\boldsymbol{n}$ 和 $\boldsymbol{v}$ 一定有 $\boldsymbol{n} \cdot \boldsymbol{v} = 0$。这种说法的依据在于。如果作用在刚体上的力是有限的，那么其加速度也一定是有限的。所以，如果 $\zeta < 0$，那么下一瞬间刚体将穿透表面。如果 $\zeta > 0$，那么上一瞬间刚体已经穿透过表面了。但是在任何时候穿透都是不被允许的，所以接触时有 $\zeta = 0$。因此我们可以推论 $\zeta \neq 0$ 意味着发生了一次冲击。接触分离加速度contact separation acceleration也是我们的研究对象，它是 $\zeta$ 的微分，可以写成如下的形式

$$ \begin{equation}\label{equa_11.3} \dot \zeta = \frac{d}{dt} \left(\boldsymbol{n} \cdot \boldsymbol{v}\right) = \boldsymbol{n} \cdot \boldsymbol{a} + \dot{\boldsymbol{n}} \cdot \boldsymbol{v} \end{equation} $$

碰撞的瞬间该值是未知的。第二项 $\dot{\boldsymbol{n}} \cdot \boldsymbol{v}$ 是已知的，可以写成关于刚体 $B$ 的位置和速度以及接触表面形状的函数。接触分离加速度 $\dot{\zeta}$ 不可能为负，否则就会产生干涉，所以有约束 $\dot{\zeta} ≥ 0$。

现在我们可以准确的描述接触约束作用了：接触要不在当前瞬间结束，要不将一直存在。The exact behaviour of the contact constraint can now be stated as follows: either the contact breaks at the current instant, or it persists.如果结束接触，那么分离加速度必定是正的，并且接触力一定为 0，因为接触已经不存在了。如果保持接触，那么分离加速度必须为 0。因此，我们有:

$$ \dot{\zeta} > 0 \quad \text{and} \quad \lambda = 0 \qquad \text{if the contact breaks ,} \\ \dot{\zeta} = 0 \quad \text{and} \quad \lambda ≥ 0 \qquad \text{if the contact persists } $$

我们可以用约束方程简洁地描述这些特性:

$$ \begin{equation}\label{equa_11.4} \dot{\zeta} ≥ 0, \qquad \lambda ≥ 0, \qquad \dot{\zeta}\lambda = 0 \end{equation} $$

接下来，我们把 $\dot{\zeta}$ 写成 $\lambda$ 的函数。这就需要用到刚体动力学，刚体 $B$ 的运动方程为:

$$ \begin{equation}\label{equa_11.5} \boldsymbol{I}\boldsymbol{a} + \boldsymbol{v} \times^* \boldsymbol{I}\boldsymbol{v} = \boldsymbol{f} + \boldsymbol{n} \lambda \end{equation} $$

其中 $\boldsymbol{f}$ 表示作用在刚体上的所有力，不仅仅是接触力。从上式可以写出 $\boldsymbol{a}$ 关于 $\lambda$ 的方程，有:

$$ \begin{equation}\label{equa_11.6} \boldsymbol{a} = \boldsymbol{I}^{-1}\left(\boldsymbol{n} \lambda + \boldsymbol{f} - \boldsymbol{v} \times^* \boldsymbol{I}\boldsymbol{v}\right) \end{equation} $$

将该式代入式($\ref{equa_11.3}$)，有:

$$ \begin{equation}\label{equa_11.7} \begin{array}{l} \dot \zeta & = & \boldsymbol{n} \cdot \boldsymbol{I}^{-1}\left(\boldsymbol{n} \lambda + \boldsymbol{f} - \boldsymbol{v} \times^* \boldsymbol{I}\boldsymbol{v}\right) + \dot{\boldsymbol{n}} \cdot \boldsymbol{v} \\ & = & M \lambda + d \end{array} \end{equation} $$

其中

$$ \begin{equation}\label{equa_11.8} M = \boldsymbol{n} \cdot \boldsymbol{I}^{-1} \boldsymbol{n} \end{equation} $$ $$ \begin{equation}\label{equa_11.9} d = \boldsymbol{n} \cdot \boldsymbol{I}^{-1}\left(\boldsymbol{f} - \boldsymbol{v} \times^* \boldsymbol{I}\boldsymbol{v}\right) + \dot{\boldsymbol{n}} \cdot \boldsymbol{v} \end{equation} $$

因此根据式($\ref{equa_11.4},\ref{equa_11.7}$)可以解出 $\dot{\zeta}$ 和 $\lambda$:

$$ \begin{equation}\label{equa_11.10} \dot{\zeta} = d \quad \text{and} \quad \lambda = 0 \qquad \text{if d ≥ 0} \\ \dot{\zeta} = 0 \quad \text{and} \quad \lambda = -d/M \qquad \text{if d < 0} \end{equation} $$

因为 $\boldsymbol{I}$ 是正定的，所以 $M$ 也一定是正数。解出$\lambda$后，就可以写出式($\ref{equa_11.1}$)和($\ref{equa_11.6}$)中的 $\boldsymbol{f}_c, \boldsymbol{a}$。观察上式会发现，$d$ 是 $\boldsymbol{f}$ 的线性函数，而 $\lambda$ 只是 $d$ 的分段线性函数。因此 $B$ 的加速度并不是作用力的线性函数，而是分段线性的picewise-linear function。这是接触动力学与等式约束的系统动力学的本质区别。

11.2 多点接触 Multiple Point Contact

我们现在将§11.1扩展到单个刚体与固定表面发生多个无摩擦接触的情况。图 11.2 中展示了一个这样的系统。假设一共有 $n_c$ 个接触点，并从 1 编号到 $n_c$，第 $i$ 个接触点标记为 $C_i$，其接触法向量为 $\boldsymbol{n}_i$。此外在接触瞬间刚体上恰好于 $C_i$ 重合的点被记为 $C_i'$。

图 11.2. 一个刚体与一个固定表面发生多点接触。

固定表面会在每个接触点上给刚体施加一个约束力。第 $i$ 个接触点的约束力为 $\boldsymbol{n}_i \lambda_i$，其中 $\lambda_i$ 是未知的接触力大小，它约束点 $C_i'$ 不要穿过接触面。因为接触力只能排斥点 $C_i'$，所以它一定沿着接触法向量 $\boldsymbol{n}_i$的正向，因此有约束 $\lambda_i ≥ 0$。如果 $\boldsymbol{f}_c$ 是作用在刚体上的约束力的合力，那么有:

$$ \begin{equation}\label{equa_11.11} \boldsymbol{f}_c = \sum_{i = 1}^{n_c} \boldsymbol{n}_i \lambda_i \end{equation} $$

令 $\zeta_i$ 表示第 $i$ 个接触点的分离速度。它是点 $C_i'$ 的线速度在法线方向 $\boldsymbol{n}_i$ 的分量，即:

$$ \begin{equation}\label{equa_11.12} \zeta_i = \boldsymbol{n}_i \boldsymbol{v} \end{equation} $$

虽然整个系统中只有一个移动的刚体，但是每个接触点都有它各自的分离速度。在接触瞬间，各个分离速度都必须为零。这意味着刚体的速度必须满足等式

$$ \boldsymbol{n}_i \cdot \boldsymbol{v} = 0 \quad \left(i = 1, \cdots, n_c\right) $$

如果接触法向量分布在整个$F^6$空间下，那么上式的唯一解就是 $\boldsymbol{v} = \boldsymbol{0}$，但是这样刚体就不能移动了。实际上刚体可能会加速远离，会有一个或者多个接触点被打破。

接触点$i$的分离加速度则是分离速度的微分，可以写成

$$ \begin{equation}\label{equa_11.13} \dot \zeta_i = \frac{d}{dt} \left(\boldsymbol{n}_i \cdot \boldsymbol{v}\right) = \boldsymbol{n}_i \cdot \boldsymbol{a} + \dot{\boldsymbol{n}_i} \cdot \boldsymbol{v} \end{equation} $$

当$\zeta_i = 0$时，$\dot{\zeta}_i$的数值不能为负，因为这样将导致在接触点 $i$ 出产生局部的穿透，所以我们需要 $\dot{\zeta}_i ≥ 0$。现在我们用形式化的语言准确地描述一下这种接触行为。在碰撞瞬间，每个接触点要么立即脱离，要么保持接触。at the current instant, each contact either breaks or it persists.如果第 $i$ 个接触点脱离接触，那么有 $\dot{\zeta} > 0, \lambda_i = 0$，否则 $\dot{\zeta}_i = 0, \lambda_i ≥ 0$。因此，我们有

$$ \begin{equation}\label{equa_11.14} \dot{\zeta}_i ≥ 0, \qquad \lambda_i ≥ 0, \qquad \dot{\zeta}_i\lambda_i = 0 \qquad \left(i = 1, \cdots, n_c\right) \end{equation} $$

不幸的是，我们现在并不知道哪个接触点将脱离，哪个会保持。把脱离接触点和保持接触点找出来也是我们求解的一项内容。现在我们再引入三个量, $\boldsymbol{N}, \boldsymbol{\lambda}, \boldsymbol{\zeta}$，它们的定义如下

$$ \begin{equation}\label{equa_11.15} \boldsymbol{N} = \begin{bmatrix} \boldsymbol{n}_1 & \boldsymbol{n}_2 & \cdots & \boldsymbol{n}_{n_c} \end{bmatrix}, \qquad \boldsymbol{\lambda} = \begin{bmatrix} \lambda_1 \\ \lambda_2 \\ \vdots \\ \lambda_{n_c} \end{bmatrix}, \qquad \boldsymbol{\zeta} = \begin{bmatrix} \zeta_1 \\ \zeta_2 \\ \vdots \\ \zeta_{n_c} \end{bmatrix} \end{equation} $$

其中 $\boldsymbol{N}$ 是一个 $6 \times n_c$ 的矩阵，另外两个都是具有 $n_c$ 个元素的向量。借助这些符号，我们可以将式($\ref{equa_11.11}$), ($\ref{equa_11.13}$), ($\ref{equa_11.14}$)写成如下的形式:

$$ \begin{equation}\label{equa_11.16} \boldsymbol{f}_c = \boldsymbol{N} \boldsymbol{\lambda} \end{equation} $$ $$ \begin{equation}\label{equa_11.17} \dot{\boldsymbol{\zeta}} = \boldsymbol{N}^T \boldsymbol{a} + \dot{\boldsymbol{N}}^T \boldsymbol{v} \end{equation} $$ $$ \begin{equation}\label{equa_11.18} \dot{\boldsymbol{\zeta}} ≥ \boldsymbol{0}, \quad \boldsymbol{\lambda} ≥ \boldsymbol{0}, \quad \dot{\boldsymbol{\zeta}}^T \boldsymbol{\lambda} = 0 \end{equation} $$

形如 $\boldsymbol{a} ≥ \boldsymbol{b}$ 的表达式中，$\boldsymbol{a}, \boldsymbol{b}$都是向量，只有当所有的元素 $i$ 都有 $a_i ≥ b_i$ 时，不等式才成立。约束 $\dot{\boldsymbol{\zeta}}\boldsymbol{\lambda} = 0$ 结合式($\ref{equa_11.18}$)中的另外两项，意味着对于所有 $i$ 都有 $\dot{\zeta}_i \lambda_i = 0$。刚体$B$的运动方程为:

$$ \boldsymbol{I}\boldsymbol{a} + \boldsymbol{v} \times^* \boldsymbol{I}\boldsymbol{v} = \boldsymbol{f} + \boldsymbol{N}\boldsymbol{\lambda} $$

从该式中可以整理出 $\boldsymbol{a}$ 关于 $\boldsymbol{\lambda}$ 的方程

$$ \begin{equation}\label{equa_11.19} \boldsymbol{a} = \boldsymbol{I}^{-1}\left(\boldsymbol{N}\boldsymbol{\lambda} + \boldsymbol{f} - \boldsymbol{v} \times^* \boldsymbol{I}\boldsymbol{v}\right) \end{equation} $$

将之代入式($\ref{equa_11.17}$) 有

$$ \begin{equation}\label{equa_11.20} \dot{\boldsymbol{\zeta}} = \boldsymbol{M}\boldsymbol{\lambda} + \boldsymbol{d} \end{equation} $$ 其中 $$ \begin{equation}\label{equa_11.21} \boldsymbol{M} = \boldsymbol{N}^T\boldsymbol{I}^{-1}\boldsymbol{N} \end{equation} $$ $$ \begin{equation}\label{equa_11.22} \boldsymbol{d} = \boldsymbol{N}^T\boldsymbol{I}^{-1}\left(\boldsymbol{f} - \boldsymbol{v} \times^* \boldsymbol{I}\boldsymbol{v}\right) + \dot{\boldsymbol{N}}^T\boldsymbol{v} \end{equation} $$

现在我们可以先根据式($\ref{equa_11.18}$)和($\ref{equa_11.20}$)得到 $\boldsymbol{\lambda}$，再根据式($\ref{equa_11.19}$)写出刚体 $B$ 的加速度$\boldsymbol{a}$。与可以通过分类讨论求解的式($\ref{equa_11.4}$)和($\ref{equa_11.7}$)不同的是，式($\ref{equa_11.18}$)和($\ref{equa_11.20}$)需要一个特别的算法来求解。我们在这里做一些必要的说明，详细的算法将在§11.5中详细。

如果 $\boldsymbol{d} ≥ \boldsymbol{0}$，那么一个可能的解就是 $\boldsymbol{\lambda} = \boldsymbol{0}$
如果 $\boldsymbol{M}$ 是正定的，那么就刚好有一个解。否则可能有一个解、没有解，也可能有无穷多解。
如果 $\boldsymbol{\lambda}$ 有多个解，那么它们得到的 $\boldsymbol{a}$ 都一样。

从式($\ref{equa_11.21}$)可以看出 $\boldsymbol{M}$ 是对称的，并且是半正定的。只有当接触法向量是线性无关的时候，$\boldsymbol{M}$ 才是正定的。因此当接触法向量是线性相关的时候，$\boldsymbol{\lambda}$才有可能无解或者多解。

图 11.3. 一个无解的接触系统

Example 11.1:如果式($\ref{equa_11.18}$)和($\ref{equa_11.20}$)无解，那么这意味着任何 $\lambda$ 都将无法阻止违反接触约束的情况发生。左图 11.3 中描述了一种 2D 的无解接触系统。图中画的是一个在插槽中滑动的圆盘。在线 $L$ 的左侧，槽壁是直的并且其宽度与圆盘的直径相等。此时，圆盘与插槽之间有两个接触点，其接触法向量 $\boldsymbol{n}_1, \boldsymbol{n}_2$ 如图所示。这两个法向量存在关系 $\boldsymbol{n}_2 = - \boldsymbol{n}_1$，因此它们是线性相关的。在线 $L$ 的右侧，槽壁是向内弯曲的圆弧，使得插槽变窄。此时，圆盘的圆心 $D$ 可以出现在线 $L$ 上或者它的左侧，但是不能到达 $L$ 的右侧，因为插槽太窄了because the slot is too narrow。

现在，我们考虑 $D$ 位于线 $L$ 上的情况。此时圆盘已经无法再向右移动了，但是两个接触法向量分别过圆心指向上方和下方，它们无法影响圆盘的水平移动。如果对圆盘施加了一个力，将其推向右侧，那么我们就会遇到一个矛盾的情形。向右运动是不可能的了，但是接触力还无法阻止它。如果在仿真中出现这种情况，一种解决方案是允许 $D$ 稍微向 $L$的右侧移动一点，这样两个接触法向量就会改变方向，进而能够阻止圆盘向右更进一步。

如果 $D$ 按照图中所示那样，以线速度 $\boldsymbol{v}$ 到达线$L$上，那么需要一个冲量来阻止圆盘的运动。同样的，仿真必须允许$D$略微超过$L$，然后才能施加此冲量。在这两种情况下，仿真都必须容忍圆盘和槽之间存在微小的穿透。

给定法向量$\boldsymbol{n}_2 = -\boldsymbol{n}_1$，那么$\boldsymbol{M}$将具有$\begin{bmatrix} m & -m \\ -m & m \end{bmatrix}$的形式，其中 $m$ 是一个正数。根据式($\ref{equa_11.20}$)有

$$ \dot{\zeta}_1 + \dot{\zeta}_2 = d_1 + d_2 $$

如果上式有解，那么必须有 $\dot{\zeta}_1 + \dot{\zeta}_2 ≥ 0$。因此无解的条件是 $d_1 + d_2 < 0$。

11.3 有接触的刚体系统 A Rigid-Body System with Contacts

我们现在考虑一个具有多个无摩擦接触点的一般刚体系统。它与上一小节中的系统有一个比较大的区别，一般刚体系统的运动方程是在关节空间下的，具有如下的形式

$$ \begin{equation}\label{equa_11.23} \boldsymbol{H}\ddot{\boldsymbol{q}} + \boldsymbol{C} = \boldsymbol{\tau} + \boldsymbol{\tau}_c \end{equation} $$

其中，$\boldsymbol{\tau}_c$ 是一个关节空间下的力，用于表示所有接触力的合力。$\ddot{\boldsymbol{q}}$就会受到接触的运动约束。因此有必要将各个接触力和加速度转换到关节空间下，这样才能将他们整合进运动方程中。

另一个不同之处是接触可以出现在系统中不同的刚体之间，因此有必要先识别出系统中存在接触的刚体对。为了方便区分，我们采用前驱 predecessor和后继 successor来表示接触的两个刚体。接触力被定义为从前驱传递给后继的力，分离加速度则是后继相对于前驱的加速度。套用这一约定，那么图 11.1和图 11.2中，固定表面是前驱，刚体 $B$就是后继。注意，接触可以发生在两个移动的刚体之间，也可以是移动的刚体于固定基座之间的接触。

假设系统中一共有 $n_c$ 个接触，我们从 1 到 $n_c$ 对它们进行编码。用两个整数的数组 $pc$ 和 $sc$ 来保存接触的刚体，对于第 $i$ 个接触， $pc(i)$ 表示该接触的前驱刚体编号，$sc(i)$ 则是后继刚体编号。这样每个接触都已用一个接触点 $C_i$ 来描述，改点位于前驱的表面上，对应的，用 $C_i'$ 表示接触瞬间在后继刚体上恰好于 $C_i$ 重合的点。接触点的法向量记为 $\boldsymbol{n}_i$， which is a unit spatial force acting along the line of the contact normal. $\boldsymbol{n}_i$是从前驱指向后继的，所以用一个正的标量乘 $\boldsymbol{n}_i$ 的意义是两个刚体在第$i$个接触点局部地相互排斥。

假设接触没有摩擦，那么在接触点 $i$ 处存在的任何接触力都必须是 $\boldsymbol{n}_i$ 的标量倍数。此外，接触约束要求作用力必须是排斥的，因此这个标量倍数必须是正的。我们引入变量 $\lambda_i$ 来表示接触点 $i$ 处未知的接触力大小，它必须满足约束 $\lambda_i ≥ 0$。接触点 $i$ 处的力是从前驱 $pc(i)$ 传递到后继 $sc(i)$ 的。因此，它相当于力 $\boldsymbol{n}_i \lambda_i$ 作用在前驱 $sc(i)$ 上，作用在后继 $pc(i)$ 的力则是 $-\boldsymbol{n}_i\lambda_i$。为了将这对力转换为关节空间下的等效力，这里我们使用一般公式 $\boldsymbol{\tau} = \boldsymbol{J}_i^T \boldsymbol{f}$ ，其中 $\boldsymbol{f}$ 是施加于刚体 $i$ 的空间力，$\boldsymbol{\tau}$ 则是等效的关节空间力， $\boldsymbol{J}_i$ 是刚体 $i$ 的雅可比矩阵。如果 $\boldsymbol{\tau}_{ci}$ 表示由接触 $i$ 产生的关节空间力，那么它的方程为

$$ \begin{equation}\label{equa_11.24} \boldsymbol{\tau}_{ci} = \left(\boldsymbol{J}_{sc(i)}^T - \boldsymbol{J}_{pc(i)}^T\right) \boldsymbol{n}_i \lambda_i \end{equation} $$

此时我们得到了一个新的量 $\boldsymbol{t}_i$

$$ \begin{equation}\label{equa_11.25} \boldsymbol{t}_i = \left(\boldsymbol{J}_{sc(i)}^T - \boldsymbol{J}_{pc(i)}^T\right) \boldsymbol{n}_i \end{equation} $$

我们可以将它看做关节空间下接触点 $i$ 得接触法向量。将式($\ref{equa_11.25}$) 代入式($\ref{equa_11.24}$) 有 $\boldsymbol{\tau}_{ci} = \boldsymbol{t}_i \lambda_i$。表示总体接触的关节空间力，即所有接触力的合力，现在可以写成

$$ \begin{equation}\label{equa_11.26} \boldsymbol{\tau}_c = \sum_{i = 1}^{n_c} \boldsymbol{t}_i \lambda_i \end{equation} $$

令 $\zeta_i$ 表示接触点 $i$ 的分离速度。由于两个刚体的速度都可能非零，我们对式($\ref{equa_11.12}$)进行了扩展，将分离速度定义为$C_i'$相对于$C_i$的线速度在法向上的分量，即:

$$ \begin{equation}\label{equa_11.27} \zeta_i = \boldsymbol{n}_i \cdot \left(\boldsymbol{v}_{sc(i)} - \boldsymbol{v}_{pc(i)}\right) \end{equation} $$

现在，我们应用一般方程 $\boldsymbol{v}_i = \boldsymbol{J}_i \dot{\boldsymbol{q}}$，将 $\zeta_i$ 写成关于关节空间速度 $\dot{\boldsymbol{q}}$ 的方程。其中 $\boldsymbol{v}_i$ 和 $\boldsymbol{J}_i$ 分别是刚体 $i$ 的速度和雅可比矩阵。如此，式($\ref{equa__11.27}$)可以改写为

$$ \zeta_i = \boldsymbol{n}_i \cdot \left(\boldsymbol{J}_{sc(i)} - \boldsymbol{J}_{pc(i)}\right) \dot{\boldsymbol{q}} $$

结合式($\ref{equa_11.25}$)，可以写出方程($\ref{equa_11.12}$)在关节空间下的形式:

$$ \begin{equation}\label{equa_11.28} \zeta_i = \boldsymbol{t}_i^T \cdot \dot{\boldsymbol{q}} \end{equation} $$

得到关节空间下的分离速度表达式之后，对其进行微分就得到了分离加速度:

$$ \begin{equation}\label{equa_11.29} \dot{\zeta}_i = \frac{d}{dt}\left(\boldsymbol{t}_i^T \cdot \dot{\boldsymbol{q}}\right) = \boldsymbol{t}_i^T \ddot{\boldsymbol{q}} + \dot{\boldsymbol{t}}_i^T \dot{\boldsymbol{q}} \end{equation} $$

按照接触约束的限制，在接触瞬间有 $\zeta_i = 0$，并且 $\dot{\zeta}_i ≥ 0$。上式的第二项$\dot{\boldsymbol{t}}_i^T \dot{\boldsymbol{q}}$可以通过下面的表达式计算:

$$ \begin{equation}\label{equa_11.30} \dot{\boldsymbol{t}}_i^T \dot{\boldsymbol{q}} = \boldsymbol{n}_i \cdot \left(\boldsymbol{a}_{sc(i)}^{vp} - \boldsymbol{a}_{pc(i)}^{vp}\right) + \dot{\boldsymbol{n}}_i \left(\boldsymbol{v}_{sc(i)} - \boldsymbol{v}_{pc(i)} \right) \end{equation} $$

其中，$\boldsymbol{a}_i^{vp}$ 是刚体 $i$ 的速度积加速度velocity-product acceleration，即 $\dot{\boldsymbol{J}}_i \dot{\boldsymbol{q}}$。现在我们引入式($\ref{equa_11.15}$)中的向量 $\boldsymbol{\lambda},\boldsymbol{\zeta}$，并定义一个新的 $n \times n_c$ 的矩阵 $\boldsymbol{T}$

$$ \begin{equation}\label{equa_11.31} \boldsymbol{T} = \begin{bmatrix} \boldsymbol{t}_1 & \boldsymbol{t}_2 & \cdots \boldsymbol{t}_{n_c} \end{bmatrix} \end{equation} $$

那么式($\ref{equa_11.26}$)和($\ref{equa_11.29}$)可以写作

$$ \begin{equation}\label{equa_11.32} \boldsymbol{\tau}_c = \boldsymbol{T}\boldsymbol{\lambda} \end{equation} $$ $$ \begin{equation}\label{equa_11.33} \dot{\boldsymbol{\zeta}} = \boldsymbol{T}^T\ddot{\boldsymbol{q}} + \dot{\boldsymbol{T}}^T \dot{\boldsymbol{q}} \end{equation} $$

这两个表达式用于替换式($\ref{equa_11.16}$)($\ref{equa_11.17}$)，但是关于 $\boldsymbol{\lambda}$ 和 $\dot{\boldsymbol{\zeta}}$ 的约束仍然和式($\ref{equa_11.18}$)一致。最后，要把 $\dot{\boldsymbol{\zeta}}$ 写成关于 $\boldsymbol{\lambda}$ 的表达式。我们将式($\ref{equa_11.32}$)代入式($\ref{equa_11.23}$)，将$\ddot{\boldsymbol{q}}$整理到方程的左侧，有

$$ \ddot{\boldsymbol{q}} = \boldsymbol{H}^{-1}\left(\boldsymbol{T}\boldsymbol{\lambda} + \boldsymbol{\tau} - \boldsymbol{C}\right) $$ 将之代入式($\ref{equa_11.33}$)，有 $$ \begin{equation}\label{equa_11.34} \dot{\boldsymbol{\zeta}} = \boldsymbol{M}\boldsymbol{\lambda} + \boldsymbol{d} \end{equation} $$ $$ \begin{equation}\label{equa_11.35} \boldsymbol{M} = \boldsymbol{T}^T\boldsymbol{H}^{-1}\boldsymbol{T} \end{equation} $$ $$ \begin{equation}\label{equa_11.36} \boldsymbol{d} = \boldsymbol{T}^T\boldsymbol{H}^{-1}\left(\boldsymbol{\tau} - \boldsymbol{C}\right) + \dot{\boldsymbol{T}}^T \dot{\boldsymbol{q}} \end{equation} $$

我们用式($\ref{equa_11.35}$)($\ref{equa_11.36}$)替换式($\ref{equa_11.21}$)($\ref{equa_11.22}$)，式($\ref{equa_11.34}$)仍然保持和($\ref{equa_11.20}$)相同的形式。实际上，这两组表达式的唯一不同之处在于式($\ref{equa_11.20}$)中$\boldsymbol{M}$的秩被表达式($\ref{equa_11.21}$)限定在 6，而式($\ref{equa_11.34}$)中$\boldsymbol{M}$的秩则没有限制。它的求解过程与§11.2完全一样，使用§11.5中描述的方法求解由($\ref{equa_11.18}$)约束的方程($\ref{equa_11.34}$)。

11.4 不等式约束 Inequality Constraints

假设 $B_1$ 和 $B_2$ 是一般刚体系统中的两个物体，$S_1$ 和 $S_2$ 是两个表面或表面贴片surface patches，其中 $S_1$ 固定在 $B_1$ 上，$S_2$ 固定在 $B_2$ 上。这两个表面之间的接触约束是不能穿透对方。假设我们有一个函数$\phi(\boldsymbol{q})$，根据 $S_1,S_2$是否分开、接触或者穿透对方，取大于、等于或者小于 0 的值。 $\phi(\boldsymbol{q}) ≥ 0$ 可以是 $S_1$ 和 $S_2$ 之间的分离距离的度量，为负数时则是它们的穿透距离。如此，接触约束可以用以下方程表示:

$$ \begin{equation}\label{equa_11.37} \phi(\boldsymbol{q}) ≥ 0 \end{equation} $$

这种形式的约束方程被称为不等式约束inequality constraint 或者说是单边约束unilateral constraint。所谓的单边约束是指，如果两个表面接触了，该约束只允许一个方向的运动，相反的那个方向的运动是不应该存在的。

图 11.4. $\phi(\boldsymbol{q}) ≥ 0$的可能情况。

根据 $\boldsymbol{q}$ 和 $\dot{\boldsymbol{q}}$ 的实际情况，不等式约束在一个刚体系统中可能产生不同的作用。为了理解这些作用，我们在图 11.4中描述了四种情况。

情况 1 的特征是 $\phi(\boldsymbol{q}) > 0$。在这种情况下，表面之间的距离大于零，因此没有接触，对系统的速度和加速度没有约束，也不产生接触力。此情况下的不等式约束对系统的当前瞬时的动力学没有影响，可以视为未激活。

情况 2a 的特征是 $\phi = 0$ 并且 $\dot{\phi} < 0$。$\dot{\phi}$ 是 $\boldsymbol{q}$ 和 $\dot{\boldsymbol{q}}$ 的函数。这种情况在两个表面发生碰撞时出现，它会在两个碰撞体之间产生冲量。在碰撞瞬间之后，系统将立即处于情况 2b 或情况 3，具体取决于碰撞是弹性(反弹)还是塑性(无反弹)的 depending on whether the collision is elastic (bounce) or plastic (no bounce)。情况 2a 仅持续一瞬间，但它会导致系统速度发生阶跃变化，必须使用冲量动力学方程来计算。

情况 2b 的特征是 $\phi = 0$ 并且 $\dot{\phi} > 0$。这种情况下表面接触，但它们正以正分离速度飞离。这种情况会在碰撞冲击之后立即发生，或者是在几何接触丢失时发生(参见 §11.6)。它只持续一个瞬间，将在当前瞬间之后立即转换为情况 1。情况 2b 对系统的瞬时动力学没有影响，可以像情况 1 一样处理。

情况 3 的特征是 $\phi = 0$ 并且 $\dot{\phi} = 0$，是一种长时间保持接触的状态。在这种情况下，两个表面接触，并且它们的分离速度为零。因此，分离加速度被限制为非负，并且会产生接触力作用于系统，施加接触约束。当前时刻，两个表面可能加速远离彼此$\ddot{\phi} > 0$，或者它们保持接触$\ddot{\phi} = 0$。 $\ddot{\phi} > 0$时，系统将在当前时刻之后立即转换为情况 1，并且接触力将为变为零。$\ddot{\phi} = 0$是，系统将保持在情况 3，并且接触力将起作用以防止 $\ddot{\phi} < 0$

从这一表述中，我们可以发现 §11.1 到 §11.3 都涉及到了情况3的不等式约束。此外对 $\phi(\boldsymbol{q})$ 微分还有:

$$ \begin{equation}\label{equa_11.38} \dot{\phi} = \boldsymbol{t}^T \dot{\boldsymbol{q}} \end{equation} $$ $$ \begin{equation}\label{equa_11.39} \ddot{\phi} = \boldsymbol{t}^T \ddot{\boldsymbol{q}} + \dot{\boldsymbol{t}}^T \dot{\boldsymbol{q}} \end{equation} $$ $$ \begin{equation}\label{equa_11.40} \boldsymbol{t}^T = \frac{\partial \phi}{\partial \boldsymbol{q}} \end{equation} $$

将这些方程与式($\ref{equa_11.28}$) 和 ($\ref{equa_11.29}$) 进行比较，可以看出 $\zeta_i$ 和 $\dot{\zeta_i}$ 对应于 $\dot{\phi}_i$ 和 $\ddot{\phi}_i$，用于选择合适的函数 $\phi_i(q)$。同样，式($\ref{equa_11.25}$) 中的 $\boldsymbol{t}_i$ 对应于 $(\partial \phi_i / \partial \boldsymbol{q})^T$。

11.5 求解接触方程 Solving Contact Equations

根据 §11.3，点接触约束下的刚体系统的运动方程是:

$$ \begin{equation}\label{equa_11.41} \boldsymbol{H}\ddot{\boldsymbol{q}} + \boldsymbol{C} = \boldsymbol{\tau} + \boldsymbol{T}\boldsymbol{\lambda} \end{equation} $$

其中 $\boldsymbol{\lambda}$ 是如下问题的解

$$ \begin{equation}\label{equa_11.42} \dot{\boldsymbol{\zeta}} = \boldsymbol{M}\boldsymbol{\lambda} + \boldsymbol{d}, \quad \dot{\boldsymbol{\zeta}} ≥ \boldsymbol{0}, \quad \boldsymbol{\lambda} ≥ \boldsymbol{0}, \quad \dot{\boldsymbol{\zeta}} \boldsymbol{\lambda} = 0 \end{equation} $$

§11.1 和 §11.2 中涉及到的方程只是一些特殊情况，它们都是用单个刚体的运动方程来替代这里的式($\ref{equa_11.41}$)。式($\ref{equa_11.41}$) 在前面的章节中已经介绍过了，但式($\ref{equa_11.42}$) 是新的。实际上，式($\ref{equa_11.42}$)中的方程和不等式集定义了一个标准数学问题，称为线性互补问题Linear Complementarity Problem, LCP。这个问题的数学原理和几种求解算法，可以在 Cottle et al. (1992) 和 Cottle and Dantzig (1968) 中找到。如果 $\boldsymbol{M}$ 是正定的，还有特别的求解算法 Featherstone (1987)。

在接触动力学应用中，$\boldsymbol{M}$ 始终是对称的半正定矩阵，并且如果 $\boldsymbol{T}$ 的列(即接触法向量)线性无关，则它将是正定的。对称半正定矩阵的 LCP 具有以下特殊性质：

如果 $\boldsymbol{M}$ 是正定的，那么该问题将只有一个解。否则可能无解、有单解、或者多解。
如果存在一个解，那么 $\boldsymbol{T}\boldsymbol{\lambda}$ 和 $\boldsymbol{\zeta}$ 的值是唯一的。即，如果存在多解则那么它们仅在 $\boldsymbol{\lambda}$ 的值上有所不同，并且差异存在于 $\boldsymbol{T}$ 的零空间中。
式($\ref{equa_11.42}$) 中的 LCP 问题于如下的二次规划问题quadratic program等价: 式($\ref{equa_11.42}$)是式($\ref{equa_11.43}$)解的 Kuhn-Tucker 条件。 $$ \begin{equation}\label{equa_11.43} \begin{array}{ll} \text{minimize:} & \frac{1}{2} \boldsymbol{\lambda}^T\boldsymbol{M}\boldsymbol{\lambda} + \boldsymbol{\lambda}^T\boldsymbol{d} \\ \text{subject to:} & \boldsymbol{\lambda} ≥ \boldsymbol{0} \end{array} \end{equation} $$

式($\ref{equa_11.42}$)和式($\ref{equa_11.43}$)有相同的解，式($\ref{equa_11.43}$)的优势在于，二次规划的求解器比 LCP 的求解器应用更广泛。 Lötstedt (1982) 中还提到了另外两个公式。其中之一是:

$$ \begin{equation}\label{equa_11.44} \begin{array}{ll} \text{minimize:} & \frac{1}{2} \left(\ddot{\boldsymbol{q}} - \boldsymbol{H}^{-1}\left(\boldsymbol{\tau} - \boldsymbol{C}\right)\right)^T \boldsymbol{H} \left(\ddot{\boldsymbol{q}} - \boldsymbol{H}^{-1}\left(\boldsymbol{\tau} - \boldsymbol{C}\right)\right) \\ \text{subject to:} & \boldsymbol{T}^T\ddot{\boldsymbol{q}} + \dot{\boldsymbol{T}}^T\dot{\boldsymbol{q}} ≥ \boldsymbol{0} \end{array} \end{equation} $$

这也是一个二次规划，但最小化的量是 $\ddot{\boldsymbol{q}}$ 而不是 $\boldsymbol{\lambda}$。如果存在唯一解，应用该公式可以求出。并且如果 $n_c > n$ 它的计算效率可能还要高一些，但从 $\ddot{\boldsymbol{q}}$ 恢复 $\boldsymbol{\lambda}$ 并不简单。式($\ref{equa_11.44}$) 可被看做高斯最小约束原理Gauss' Principle of least constraint的推广，适用于具有不等式约束的刚体系统。

如果有多个接触点，那么与使用Chapter 8中提及的技术构造一组等效的等式约束相比，求解式($\ref{equa_11.42}$)和($\ref{equa_11.43}$)的计算成本要相对大一些。因此，最好尽量减少求解式($\ref{equa_11.42}$)和($\ref{equa_11.43}$)的次数。实现此目的的程序如表 11.1 所示。在这个过程中，仿真需要维护一组当前接触点集合和一组激活接触点集合，后者是前者的子集。当前接触点集包含所有处于情况 3 的接触点(如图 11.4 所示)，并且$\dot{\zeta}_i = 0$，即 $\ddot{\phi}_i = 0$。如果当前接触点满足 $\dot{\zeta}_i > 0$，则认为它在当前时刻已经脱离，并将其从集合中删除。

Tabel 11.1. 接触动力学仿真的一般过程。

向前进行时间积分，将激活的接触当作等式约束处理，并忽略其他类型的接触约束。
积分的过程中需要监控系统中两类事件：几何事件(接触增益和损失)geometric events(contact gains and losses)和负接触力negative contact forces。
如果在最近一次积分过程中检测到一个或多个此类事件，那么就向前对系统进行插值，直到最早的那个事件发生的时刻。
如果是一个接触增益事件，比如碰撞，那么就要用到§11.7中描述的冲击动力学， and identify the new set of current contacts and the new set of active contacts.
若是一个几何接触丢失事件，则从当前和激活接触集合中删除丢失的接触。
若是负接触力事件，则构建并求解方程($\ref{equa_11.42}$)和($\ref{equa_11.43}$)，并确定新的当前和激活接触集合。
回到第一步

激活接触点集是一组 $range(\boldsymbol{T})$ 的接触法线构成的一组基The set of active contacts is a set whose contact normals form a basis on range(T)，其中包含了所有接触力为正的接触点，也就是所有满足 $\lambda_i > 0$ 的接触点。如果我们将激活接触视为等式约束，那么下面这个命题为真——只要接触力变量保持非负，状态就不会发生变化。因此，在激活接触上检测到负 $\lambda_i$ 时，或发生碰撞时，我们就可以解出方程($\ref{equa_11.42}$)和式($\ref{equa_11.43}$)。负的 $\lambda_i$ 总是会导致激活接触点集发生变化，但不一定会改变当前接触点集。

大多数求解 LCP 和二次规划问题的算法都会返回一个的基本解basic solution，该解中非零变量的数量最少which is a solution having the smallest possible number of nonzero variables。式($\ref{equa_11.42}$)和式($\ref{equa_11.43}$)的基本解具有一个特性，与正接触力变量相关的接触法线是线性独立的。给定方程($\ref{equa_11.42}$)和式($\ref{equa_11.43}$)的基本解，新的当前接触点集将满足 $\dot{\zeta}_i = 0$，新的激活接触点集将满足 $\lambda_i > 0$。在极少数情况下，该集合不能构成一组基，此时需要补充满足 $\dot{\zeta}_i = \lambda_i = 0$ 的接触。

积分时间步长的插值

我们有必要解释一下积分时间步长可以插值这件事情。假设我们需要对微分方程 $\dot{y} = f(y, t)$ 从 $t_0$ 积分到 $t_1$，其中 $t_1 = t_0 + h$，而 $h$ 是积分步长。许多数值积分方法都是通过在区间 $[t_0, t_1]$ 上拟合 $\dot{y}$ 的多项式，并将该多项式的积分到 $y(t_0)$ 上实现的。这些方法具有一般形式:

$$ \begin{equation}\label{equa_11.45} \begin{array}{l} \dot{y}(t) = p(t), \quad t_0 ≤ t ≤ t_1 \\ y_1 = y_0 + \int_{t_0}^{t_1} p(t) dt \end{array} \end{equation} $$

其中，$y_0 = y(t_0), y_1 = y(t_1)$，$p(t)$ 是一个多项式。$p$ 的阶数比算法的阶数少一 The degree of p is one less than the order of the method. 因此我们可以用如下的公式计算任意中间值 $t$ 的 $y(t)$。

$$ \begin{equation}\label{equa_11.46} y(t) = y_0 + \int_{t_0}^{t} p(t) dt \end{equation} $$

举一个具体的例子，欧拉积分法通过在积分时间步长上用常数近似 $\dot{y}$ 来实现。该方法的公式为

$$ \begin{equation}\label{equa_11.47} k = f(y_0, t_0) \\ y_1 = y_0 + hk \end{equation} $$

这意味着 $p(t) = k$。因此插值多项式为

$$ \begin{equation}\label{equa_11.48} y(t) = y_0 + (t - t_0) k \end{equation} $$

令 $\delta = (t − t_0 )/h$ 为插值变量，当 $t$ 从 $t_0$ 变化到 $t_1$ 时，它将从 0 变化到 1。以 $\delta$ 表示的欧拉方法的插值多项式为

$$ \begin{equation}\label{equa_11.49} y(\delta) = y_0 + hk\delta \end{equation} $$

再来看一个更复杂的例子，一种 Heun 积分法(Gear，1971)的公式为:

$$ \begin{equation}\label{equa_11.50} \begin{array}{l} k_1 = f(y_0, t_0) \\ k_2 = f(y_0 + \frac{2}{3} hk_1, t_0 + \frac{2}{3}h) \\ y_1 = y_0 + h(\frac{1}{4}k_1 + \frac{3}{4}k_2) \end{array} \end{equation} $$

该方法用线性多项式来近似 $\dot{y}$，该多项式在 $t_0$ 处取值 $k_1$，在 $t_0 + \frac{2}{3}h$ 处取值 $k_2$。因此，该方法的插值多项式是二次的，如下

$$ \begin{equation}\label{equa_11.51} y(\delta) = y_0 + h\left(\left(\delta - \frac{3}{4}\delta^2\right)k_1 + \frac{3}{4}\delta^2 k_2 \right) \end{equation} $$

此类方法允许动力学仿真器对一个完整的积分时间步长内的任何中间时刻的状态变量进行插值，因此也可以将最近的时间步长任意缩短到所需的量。

11.6 接触几何 Contact Geometry

接触动力学的仿真除了动力学之外还涉及到几何的计算。到目前为止，我们几乎没有谈论过几何计算。在本节中，我们将研究接触动力学的一些几何，如形状的表示、几何事件(接触增益和损失contact gains and losses)以及边缘和表面接触。

形状

多面体是计算机里面最常用的几何形状。市面上有大量关于多面体的技术介绍，有很多创建、编辑和显式多面体的软件，有很多高效的基于多面体的碰撞检测方法。但很不幸，多面体不太适合动力学。图 11.5 中给出了一些可能出现问题的示例。左一是一个从斜坡上滚落的球，与之对比地，左二图中是用多面体近似表示一个球。这里为了方便画图，用多边形来表示多面体。球体滚动非常平稳。而多面体的滚动，每当有新的棱角与表面接触，就会产生一次撞击。该如何处理这些碰撞呢？如果将它们视为塑性碰撞，那么每次撞击都会有能量损失。如果将它们视为弹性碰撞，那么多面体就会开始反弹。

问题出在多面体的平面和直边上。多面体在运动过程中，点、棱、面可能交替与斜坡接触。通过向外弯曲多面体的平面和直边，我们可以得到一个严格的凸面(strictly convex)，从而解决这个问题。理想情况下，这个扭曲的多面体应该非常接近一个完美的球体。即使它不完美，它滚动的时候也不会造成撞击了。

图 11.5. 一些多面体几何形状可能面临的问题。

上图 11.5 的右二描述了另一种有问题的现象，在凹陂上滑下的矩形块。如果用多面体来近似凹陂，那么每当矩形块的棱角碰到多面凹陂的转折处，都会产生一次冲击。这次的问题在于多面凹陂上突兀的棱边，解决方法就是把它们弄圆。

这两个例子可以归结为一个问题。假设 $\boldsymbol{p}$ 是物体表面上的一点，$\boldsymbol{n}(\boldsymbol{p})$ 是该点的表面法向量。在曲面上，$\boldsymbol{n}$ 随 $\boldsymbol{p}$ 连续变化，并且这种变化通过量 $\dot{\boldsymbol{n}}$ 进入运动方程。在动力学模拟中使用多面体近似曲面的问题根源在于，多面体的 $\boldsymbol{n}(\boldsymbol{p})$ 是分段常数，无法模拟原始曲面中的 $\text{d}\boldsymbol{n}/\text{d}\boldsymbol{p}$。

几何事件

我们将几何事件定义为由物体运动引起的接触状态的阶跃变化。几何事件基本上有两种：接触增益contact gain和接触丢失contact loss。碰撞是接触增益事件的一种特殊情况，在碰撞之前两个当事物体还没有接触。图 11.6 示意了这些事件。一般来说，接触增益事件会引起冲击，而接触丢失事件会导致当前接触点集减小。

图 11.6. 几何事件。

我们用动态接触损失 dynamic contact loss一词来指前面几节中研究的那种接触损失。图 11.6 中描述了，动态接触损失和几何接触损失之间的区别，前者，两个表面由于作用在系统上的力，而加速远离彼此。后者发生在分离速度发生阶跃变化时，此时接触点已经脱离了面的边缘，或者一个物体边缘已经脱离了另一个物体边缘的末端。几何接触损失事件不能通过求解运动方程来检测，只能通过几何方法检测。

检测移动物体之间的碰撞和接触增益可能是一项计算复杂度很高的运算。因为真实物理对象的精确几何模型可能包含数百、数千甚至数万个几何图元。幸运的是，学者们已经提出了许多有效的算法，感兴趣的读者可以参考Bobrow (1989); Gilbert et al. (1988); Gottschalk et al. (1996); Jimenez et al. (2001); Mirtich (1998)。

线接触和面接触

如果接触的形式是一条线或一个表面，那么它在数学上等同于无数个点接触。线或表面上的每个点都有一个接触。因此，线或表面接触可以用一组无限的点接触来描述。实际上对原始的接触状态建模并不需要这么多点。我们可以通过以下规则来获得一个最小接触集:

如果一个接触点的法向量正线性相关于集合中其它法向量，那么它不会对接触约束做出贡献，可以被移除。
If a point contact has a normal vector that is positively dependent on other normals in the set, then it does not contribute to the contact constraint, and can be removed.

对于一个向量 $\boldsymbol{v}$ 和一个向量的集合 $\{\boldsymbol{v}_1, \boldsymbol{v}_2, \cdots \}$，如果存在一组非负的标量 $a_i$ 使得 $\boldsymbol{v} = a_1 \boldsymbol{v}_1 + a_2 \boldsymbol{v}_2 + \cdots$ 成立，那么我们说向量 $\boldsymbol{v}$ 和向量集合 $\{\boldsymbol{v}_1, \boldsymbol{v}_2, \cdots\}$ 是正线性相关的。

图 11.7. 线接触和面接触的一些例子。

图 11.7 给出了一些线接触和面接触的例子。图 (a) 是一个物体上的棱和另一个物体的平面之间的线接触。在这种情况下，可以用线的两端的点接触来建模。图 (b) 是一个直边和一个直纹面之间的线接触。直纹面的方程为 $z = x tan(y)$，其中 $z$轴指向上方，$y$轴位于接触线上。在这个例子中，直纹面的曲率使每个接触点的法线指向不同的方向。此外，接触点集中的法向量都不正相关于其他法线，因此这个例子的最小接触集包含线上每个点接触。

图 (c) 是两个平面之间的面接触，其接触区域的凸包是一个多边形。凸包是包含给定形状的最小凸形。这里的凸包是灰色的五边形。我们可以用凸包的顶点来对这样的面接触建模。图 (d) 也是两个平面之间的面接触，但接触区域是一个圆盘。因此凸包也是一个圆盘。圆盘内部的每个法向量都正相关于边界上的一对法向量，但边界上的任何法向量都不正相关于集合中的其他法向量。因此，这个例子的最小接触集由边界圆上的所有点组成。

图 11.7 中的 (a) 和 (c) 涵盖了两个多面体之间所有可能的线接触和面接触。所以，两个多面体之间的任何接触状态都可以用一组有限的点接触来表示。而 (b) 和 (d) 中，理论上需要无数的点接触才能准确表达接触约束，但工程上仅使用有限数量的点，就可以获得所需精度的近似值。

11.7 冲击动力学 Impulsive Dynamics

冲量是力关于时间的积分。如果我们从$t_0$到$t_1$将一个力$\boldsymbol{f}(t)$作用到一个刚体上，那么这个刚体就会受到一个冲量$\boldsymbol{\iota}$:

$$ \begin{equation}\label{equa_11.52} \boldsymbol{\iota} = \int_{t_0}^{t_1} \boldsymbol{f}(t) \text{d} t \end{equation} $$

这种冲量的效果是改变刚体的动量，即

$$ \begin{equation}\label{equa_11.53} \boldsymbol{\iota} = \int_{t_0}^{t_1} \boldsymbol{f}(t) \text{d} t = \int_{t0}^{t1} \frac{\text{d} \boldsymbol{h}}{\text{d}t} \text{d} t = \boldsymbol{h}(t_1) - \boldsymbol{h}(t_0) \end{equation} $$

这里 $\boldsymbol{f} = \text{d}\boldsymbol{h} / \text{d} t$ 是刚体的运动方程，$\boldsymbol{h}$ 是它的动量 $\boldsymbol{h} = \boldsymbol{I}\boldsymbol{v}$。刚体在指定时间间隔内受到的冲量等于其在该时间间隔内的动量变化量。如果两个很硬的刚体发生碰撞，那么短时间内它们彼此会施加很大的接触力。如果它们的硬度增加到无穷大，那么接触力就会发散到无穷大，碰撞的时间间隔会收敛到零，但冲量仍然是有限的。因此，对于刚体动力学，我们感兴趣的是一种特殊的冲量，力 $\boldsymbol{f} / \delta t$ 在持续时间趋近于零 $\delta t \to 0$ 时的极限:

$$ \begin{equation}\label{equa_11.54} \boldsymbol{\iota} = \lim_{\delta t \to 0} \int_t^{t + \delta t} \frac{\boldsymbol{f}(t)}{\delta t} \text{d} t \end{equation} $$

本节的其余部分将讨论此类冲量。它们有一些基础特性。首先它们是力矢量，即，$F^6$ 的元素; 其次它们是由刚体之间的碰撞，或接触增益产生; 此外它们会导致刚体速度发生阶跃变化。现在我们来推导刚体的冲量运动方程。设$\boldsymbol{\iota}$是作用在一个惯量为 $\boldsymbol{I}$ 速度为 $\boldsymbol{v}$ 的刚体上的冲量，设 $\Delta \boldsymbol{v}$ 为 $\boldsymbol{\iota}$ 引起的熟读变化量。那么 $\Delta \boldsymbol{v}$ 和 $\boldsymbol{\iota}$ 的关系是

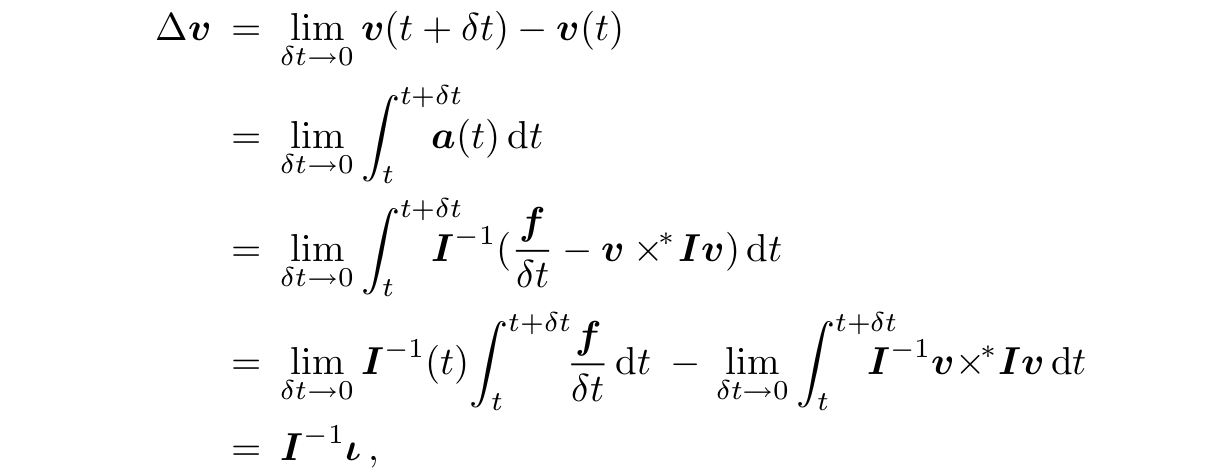
已上推导过程的在第三行是，刚体的运动方程 ($\boldsymbol{I}\boldsymbol{a} + \boldsymbol{v} \times^* \boldsymbol{I}\boldsymbol{v} = \boldsymbol{f}/\delta t$) 用于通过作用力 $\boldsymbol{f}/\delta t$ 表示其加速度。在第四行中，$\boldsymbol{I}^{−1}$只与位置有关，而位置是时间的连续函数，所以可以提取到积分之外。因此当 $\delta t \to 0$ 时，$\boldsymbol{I}^{−1}(t + \delta t) \to \boldsymbol{I}^{−1}(t)$。第四行的第二个极限等于零，因为当 $\delta t \to 0$ 时，被积函数有限。根据上式有

$$ \begin{equation}\label{equa_11.55} \boldsymbol{\iota} = \boldsymbol{I} \Delta \boldsymbol{v} \end{equation} $$

采用相同的方法，我们可以证明铰接式刚体手柄的运动方程为Using the same argument, we can show that the impulsive equation of motion for the handle of an articulated body is

$$ \begin{equation}\label{equa_11.56} \boldsymbol{\iota} = \boldsymbol{I}^A\Delta \boldsymbol{v} \end{equation} $$

其中$\boldsymbol{I}^A$是铰接式刚体手柄的惯性张量。同样的一般刚体系统的冲量运动方程为

$$ \begin{equation}\label{equa_11.57} \boldsymbol{u} = \boldsymbol{H}\Delta \dot{\boldsymbol{q}} \end{equation} $$

其中 $\boldsymbol{u}$ 是关节空间(或者说是广义)冲量，并且 $\Delta \dot{\boldsymbol{q}}$ 是关节(或广义)速度矢量的跃迁。如果 $\boldsymbol{u}$ 是由刚体 $i$ 与系统外部物体碰撞引起的，刚体 $i$ 从外部物体接收到 $\boldsymbol{\iota}$ 的冲量，这将导致其速度发生 $\Delta \boldsymbol{v}_i$ 的阶跃变化，因此我们将得到如下关系:

$$ \begin{equation}\label{equa_11.58} \boldsymbol{u} = \boldsymbol{J}_i^T \boldsymbol{\iota} \end{equation} $$ $$ \begin{equation}\label{equa_11.59} \Delta \boldsymbol{v}_i = \boldsymbol{J}_i \Delta \dot{\boldsymbol{q}} \end{equation} $$

其中$\boldsymbol{J}_i$是刚体$i$的雅可比矩阵。注意:方程($\ref{equa_11.56}$)($\ref{equa_11.57}$)和($\ref{equa_11.58}$)在数学上是正确的，但它们不一定能准确预测真实的多体系统的撞击行为。这是因为真实撞击涉及到一些在刚体假设下无法模拟的物理过程，例如通过固体和关节轴承传播的压缩波compression waves。

两体碰撞

图 11.8 中显示了两个刚体 $B_1$ 和 $B_2$ 在一点 $C$ 处发生碰撞。碰撞前它们的速度分别为 $\boldsymbol{v}_1$ 和 $\boldsymbol{v}_2$ ，碰撞后分别为 $\boldsymbol{v}_1 + \Delta \boldsymbol{v}_1$ 和 $\boldsymbol{v}_2 + \Delta \boldsymbol{v}_2$。我们最初假设接触点没有摩擦。这意味着从 $B_1$ 传递到 $B_2$ 的冲量可以表示为 $\boldsymbol{n}\lambda$的形式，其中 $\boldsymbol{n}$ 是接触法线，$\lambda ≥ 0$ 是冲量大小。因此，这两个刚体的冲量运动方程为

$$ \begin{equation}\label{equa_11.60} \Delta \boldsymbol{v}_1 = - \boldsymbol{I}_1^{-1} \boldsymbol{n} \lambda \end{equation} $$ $$ \begin{equation}\label{equa_11.61} \Delta \boldsymbol{v}_2 = \boldsymbol{I}_2^{-1} \boldsymbol{n} \lambda \end{equation} $$

令 $\zeta$ 和 $\Delta \zeta$ 分别表示撞击前 $C$ 点的分离速度以及撞击引起的分离速度阶跃变化量。它们由以下方程给出

图 11.8. 两体碰撞

$$ \begin{equation}\label{equa_11.62} \zeta = \boldsymbol{n} \cdot \left(\boldsymbol{v}_2 - \boldsymbol{v}_1\right) \end{equation} $$ $$ \begin{equation}\label{equa_11.63} \Delta \zeta = \boldsymbol{n} \cdot \left(\Delta \boldsymbol{v}_2 - \Delta \boldsymbol{v}_1\right) \end{equation} $$

这些标量必须满足 $\zeta ≤ 0$ 和 $\zeta + \Delta \zeta ≥ 0$。我们还需要另一个方程来求解这个问题。这是由恢复系数 $e$ 提供的，它是一个介于 0 和 1 之间的数字，表示撞击前后分离速度的比率。具体的，

$$ e = \frac{\zeta + \Delta \zeta}{-\zeta} $$

这意味着

$$ \begin{equation}\label{equa_11.64} \Delta \zeta = -(1 + e) \zeta \end{equation} $$

将式($\ref{equa_11.62}$)和($\ref{equa_11.63}$)代入式($\ref{equa_11.64}$)可得:

$$ \boldsymbol{n}\cdot\left(\Delta \boldsymbol{v}_2 - \Delta \boldsymbol{v}_1\right) = -(1 + e) \boldsymbol{n} \cdot \left(\boldsymbol{v}_2 - \boldsymbol{v}_1\right) $$

将式($\ref{equa_11.60}$)和($\ref{equa_11.61}$)代入该式可得

$$ \begin{equation}\label{equa_11.65} \lambda = \frac{-(1+e)\boldsymbol{n} \cdot (\boldsymbol{v}_2 - \boldsymbol{v}_1)}{\boldsymbol{n}\cdot(\boldsymbol{I}_1^{-1} + \boldsymbol{I}_2^{-1})\boldsymbol{n}} \end{equation} $$

摩擦

如果我们允许接触时存在库仑摩擦，那么系统的行为就会变得更加复杂。一般来说，我们必须考虑以下影响，切向摩擦(tangential friction)、扭转摩擦(torsional friction)、切向恢复(tangential restitution)、扭转恢复(torsional restitution)，以及在接触结束之前切向或扭转滑动运动是否被阻止。Brach (1991)研究了许多此类复杂的性质。扭转作用是指阻碍接触法线角运动的摩擦副(friction couple)。扭转作用的出现是因为真实物体并不是完全刚性的，接触表面的局部变形会导致点接触变成面接触。因此，扭转作用在较软的物体上比在较硬的物体上更明显。即便如此，扭转作用的幅度通常小于切向作用，并且通常可以忽略不计。切向和扭转恢复分别由切向和扭转方向上的局部弹性变形的恢复引起。图 11.9 给出了这些作用的一些示例。

图 11.9. 切向恢复(a)和扭转恢复(b)的一些例子。

让我们通过研究一个相对简单的摩擦碰撞例子来结束本节。我们假设两个刚体发生了如图 11.8 所示碰撞，并且没有扭转效应和切向恢复，同时切向运动被摩擦冲击阻止了。这个例子可以用与无摩擦情况几乎相同的程序来解决。

首先，切向摩擦分量会给碰撞冲量增加两个自由度，因此现在要求解的是一个有三个未知标量的函数，而不仅仅是上一节中的一个标量。于此同时，还给系统添加了两个约束，即碰撞后 $C$ 点的相对速度的切向分量必须为零。令 $\boldsymbol{\iota}$表示从 $B_1$ 传递到 $B_2$ 的总冲量，那么这两个物体的运动方程为

$$ \begin{equation}\label{equa_11.66} \Delta \boldsymbol{v}_1 = - \boldsymbol{I}_1^{-1} \boldsymbol{\iota} \end{equation} $$ $$ \begin{equation}\label{equa_11.67} \Delta \boldsymbol{v}_2 = \boldsymbol{I}_2^{-1} \boldsymbol{\iota} \end{equation} $$

我们可以将这个冲击表示为如下形式

$$ \begin{equation}\label{equa_11.68} \boldsymbol{\iota} = \boldsymbol{N} \boldsymbol{\lambda} \end{equation} $$

其中 $\boldsymbol{N} = \begin{bmatrix} \boldsymbol{n}_x & \boldsymbol{n}_y & \boldsymbol{n}_z \end{bmatrix}$ 是一个 $6 \times 3$ 的矩阵张成了所有冲量可能取值的空间。 $\boldsymbol{\lambda} = \begin{bmatrix} \lambda_x & \lambda_y & \lambda_z \end{bmatrix}^T$ 是要求的未知冲击系数向量。 $\boldsymbol{n}_z$是接触法向量，所以 $\boldsymbol{n}_z$ 和 $\lambda_z$ 对应于无摩擦情况下的$\boldsymbol{n}$和$\lambda$，而 $\boldsymbol{n}_x$ 和 $\boldsymbol{n}_y$位于接触点的切平面上，张成了所有可能得摩擦冲击可能取值的空间。这三个向量都穿过了点 $C$。令 $\boldsymbol{\zeta} = \begin{bmatrix} \zeta_x & \zeta_y & \zeta_z \end{bmatrix}^T$ 为描述两个物体在 $C$ 点的相对线速度的线速度坐标矢量。令 $\Delta \zeta = \begin{bmatrix} \Delta \zeta_x & \Delta \zeta_y & \Delta \zeta_z \end{bmatrix}^T$ 为冲击引起的 $\boldsymbol{\zeta}$ 的阶跃变化量。有

$$ \begin{equation}\label{equa_11.69} \boldsymbol{\zeta} = \boldsymbol{N}^T\left(\boldsymbol{v}_2 - \boldsymbol{v}_1\right) \end{equation} $$ $$ \begin{equation}\label{equa_11.70} \Delta \boldsymbol{\zeta} = \boldsymbol{N}^T\left(\Delta \boldsymbol{v}_2 - \Delta \boldsymbol{v}_1\right) \end{equation} $$

$\boldsymbol{\zeta}$ 和 $\Delta \boldsymbol{\zeta}$ 之间的关系部分由恢复系数给出，该系数作用于法线方向，部分由切向速度为零的条件给出。 which applies in the normal direction, and partly by the condition that the tangential velocity be brought to zero.基本上，我们有三个标量方程

$$ \zeta_x + \Delta \zeta_x = 0, \quad \zeta_y + \Delta \zeta_y = 0, \quad \zeta_z + \Delta \zeta_z = -e\zeta_z $$

可以写成矩阵的形式:

$$ \begin{equation}\label{equa_11.71} \Delta \boldsymbol{\zeta} = -(1 + \boldsymbol{E})\boldsymbol{\zeta} \end{equation} $$

其中

$$ \boldsymbol{E} = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & e \end{bmatrix} $$

为了求解这个问题，我们将式($\ref{equa_11.69}$)和($\ref{equa_11.70}$)代入式($\ref{equa_11.71}$)，得

$$ \boldsymbol{N}^T\left(\Delta \boldsymbol{v}_2 - \Delta \boldsymbol{v}_1\right) = -\left(\boldsymbol{1} + \boldsymbol{E}\right)\boldsymbol{N}^T\left(\boldsymbol{v}_2 - \boldsymbol{v}_1\right) $$

然后将式($\ref{equa_11.66}$)($\ref{equa_11.67}$)和($\ref{equa_11.68}$)代入该方程，得

$$ \begin{equation}\label{equa_11.72} \boldsymbol{\lambda} = - \left(\boldsymbol{N}^T\left(\boldsymbol{I}_1^{-1} + \boldsymbol{I}_2^{-1}\right)\boldsymbol{N}\right)^{-1} \left(\boldsymbol{1} + \boldsymbol{E}\right)\boldsymbol{N}^T \left(\boldsymbol{v}_2 - \boldsymbol{v}_1\right) \end{equation} $$

11.8 软接触 Soft Contact

到目前为止，我们仅研究了刚体对之间的接触。然而，许多物理系统都是硬体和软体的混合物，或坚硬的内心柔软的表面，或硬到足以被视为整体刚性但又足够柔软在接触过程中会发生显著的局部变形的物体。在这些情况下，必须能够模拟刚性表面与柔顺表面之间或两个柔顺表面之间的接触动力学。

我们对柔顺接触感兴趣的另一个原因是它比刚性接触更容易实现。柔顺接触碰撞时没有冲击，因此不需要计算冲击动力学。并且可以根据位置和速度数据确定接触损失，因此不存在线性互补的问题。在柔顺接触中实现库仑摩擦也更容易。出于这些原因，可能使用柔顺接触代替刚性接触可能更好。柔顺接触的主要缺点是，它会将高频动力学high-frequency dynamics引入系统，因为柔顺表面模型中存在刚性弹簧。如果这些动力学要求积分程序采取较小的步长，那么就会降低模拟速度。

本节介绍一种建模柔顺接触（包括库仑摩擦）的技术，其中柔顺表面被建模为一个一阶的动力系统，它是一个包含弹簧和阻尼器但没有质量的系统。在这样的系统中，作用力会产生速度，而施加的速度会遇到反作用力。这种技术的一大优势是它可以将刚体动力学与接触动力学分开。使得我们可以根据位置和速度变量计算接触力，然后将其作为一组已知力输入给刚体动力学程序。因此，可以将任何标准正向动力学算法与此接触模型一起使用，例如Chapter6 Chapter7 Chapter8 中描述的算法。

图 11.10. 柔顺接触模型。

接触法向量

现在我们考虑如图 11.10 所示的一维刚体系统。它由一个刚体 $B$ 和无质量表面贴片 $S$ 组成，表面贴片通过弹簧和阻尼器连接到固定基座上。变量 $z$ 和 $p$ 分别表示 $S$ 和 $B$ 的位置，$f_c$ 是从 $S$ 传递到 $B$ 的接触力。如果 $B$ 和 $S$ 接触，那么 $p = z$ 且 $f_c ≥ 0$，否则 $p > z$ 且 $f_c = 0$。假设弹簧的刚度为$K$，它对 $S$ 施加的力为 $−Kz$。阻尼器的阻尼系数为 $D$，对 $S$ 施加的力为 $−D\dot{z}$。

现在，$S$ 没有质量，所以作用于它的净力(net force)必须为零。作用于 $S$ 的三个力是 $−Kz$, $−D\dot{z}$ 和 $−f_c$，所以我们有

$$ Kz + D\dot{z} + f_c = 0 $$

对上式整理有

$$ \begin{equation}\label{equa_11.73} \dot{z} = -(Kz + f_c) / D \end{equation} $$

这是 $S$ 的运动方程。请注意，这是一个一阶微分方程，它涉及 $z$ 和 $\dot{z}$，但不涉及 $\ddot{z}$。还请注意，接触力与 $S$ 的速度线性相关，而不是其加速度。该方程中的两个未知数是 $\dot{z}$ 和 $f_c$，状态变量是 $z$。

现在我们计算 $f_c$。如果 $p > z$ 则没有接触，并且$f_c = 0$。如果 $p = z$ 则我们按如下方式进行。如果接触要保持下去，那么在当前瞬时，我们一定有 $\dot{p} = \dot{z}$。那么满足此约束的接触力为

$$ f_c = -Kz - D\dot{p} $$

如果该表达式为零或正数，那么它就是 $f_c$ 的值，此时接触确实持续存在。如果该表达式为负数，则 $f_c$ 的值应当为零，我们有 $\dot{p} > \dot{z}$，这意味着接触正在断开。将此参数组合成一个方程，我们有

$$ \begin{equation}\label{equa_11.74} f_c = \begin{cases} 0 & \mbox{if } p > z \\ \max(0, -Kz - D\dot{p}) & \mbox{if } p = z \end{cases} \end{equation} $$

方程($\ref{equa_11.74}$)和($\ref{equa_11.73}$)以及 $B$ 的运动方程(根据 $f_c$ 计算 $\ddot{p}$)，一起定义了系统的动态行为。

扩展

这种接触模型可以很容易扩展到更一般的情况。例如，要模拟两个移动物体之间的柔顺接触，只需将 $p$ 重新定义为两个物体的相对位置。要模拟两个柔顺表面之间的接触，只需对每个表面使用一个弹簧阻尼器对和一个状态变量 $z$。如果两个表面的 $K/D$ 比率相同，则可以将两个柔顺性集中在一起 then the two compliances can be lumped together。

不使用显式状态变量，我们也可以实现此模型。此技巧之所以可行，是因为当 $f_c = 0$ 时，方程($\ref{equa_11.73}$)有一个简单的解析解。因此只要有接触，就有 $z = p$，而在其他所有时间力，都有 $z = z_0 e^{−K(t−t_0 )/D}$ ，其中 $t_0$ 和 $z_0$ 分别是最近一次接触丢失发生的时间和当时 $z$ 的值。此技巧消除了对方程($\ref{equa_11.73}$)进行数值积分的需要，可能会提高计算效率。

我们也可以将非线性弹簧和阻尼器纳入该模型。这样做的好处是，非线性弹簧-阻尼器提供了碰撞固体的物理行为的更精确模型(Marhefka and Orin，1999)。另一种可能性是使用更通用的粘弹性元件(visco-elastic element)，例如与弹簧串联的弹簧-阻尼器对。但是，更复杂的模型可能需要引入额外的状态变量。

要将此模型应用于两个 3D 物体之间的点接触，我们还需要根据物体的形状和位置计算出，接触法向量 $n$ 和表示穿透深度的负值。后者给出了 $p$ 的值。如果变形很小，那么根据表面的未变形形状计算 $n$ 是合理的。$\dot{p}$ 相当于前面几节中的 $\zeta$，可以通过形式为 $\dot{p} = \boldsymbol{n} \cdot (\boldsymbol{v}_B − \boldsymbol{v}_S)$ 的方程计算得出，其中 $\boldsymbol{v}_B$ 和 $\boldsymbol{v}_S$ 是接触物体的速度。同样，$f_c$ 相当于前面几节中的 $\lambda$，传递到物体 $B$ 的空间接触力为 $\boldsymbol{n}f_c$。如果已知接触力的大小，那么可以直接从方程($\ref{equa_11.5}$)($\ref{equa_11.19}$)或($\ref{equa_11.23}$)等方程计算单个刚体或完整刚体系统的加速度。

如果接触点在柔顺表面上移动，那么弹簧和阻尼器应跟随该点一起移动。如果希望模拟在表面上移动压缩轨迹所做的功，那么可以通过切平面中的粘性摩擦项(viscous friction term)来近似该功。或者，可以在柔顺表面的固定位置嵌入一组弹簧-阻尼器对，并采用基于接触点位置的插值方法。

图 11.11. 库伦摩擦模型。

库仑摩擦

图 11.10 中的表面仅在法线方向上具有柔顺性，现在我们添加切向柔顺性，从而得到图 11.11 所示的系统。要将此模型扩展到 3D，我们必须添加第二个切向柔顺性。此附加柔顺性可用于实现库仑摩擦模型，其中摩擦力仅是位置和速度变量的函数。因此，接触法向力和摩擦力都可以在计算主刚体动力学之前结出，并且可以被正向动力学算法视为已知力。

我们引入两个新变量 $x$ 和 $v$，它们在切向上对应着 $z$ 和 $\dot{p}$。$x$ 是表面接触点从其平衡位置沿切向的位移，而 $v$ 是当前 $B$ 中与 $S$ 接触的点的切向速度，即，§11.1中定义的点 $C'$ 的切向速度。因此，$v$ 在每个时刻都对应着 $B$ 中不同的点。 $v$ 用于计算接触处的滑移速度。

我们的求解目标是，接触法向力 $f_n$ 和切向力 $f_t$，这个切向力就是摩擦力。首先根据式($\ref{equa_11.74}$)($\ref{equa_11.73}$)计算 $f_n$，有

$$ \begin{equation}\label{equa_11.75} f_n = \begin{cases} 0 & \mbox{if } p > z \\ \max(0, -K_n z - D_n \dot{p}) & \mbox{if } p = z \end{cases} \end{equation} $$ $$ \begin{equation}\label{equa_11.76} \dot{z} = -(K_n z + f_n) / D_n \end{equation} $$

其中 $K_n$ 和 $D_n$ 分别是法线方向的弹簧和阻尼系数。接下来构造切线方向 $S$ 的运动方程。使用与方程($\ref{equa_11.73}$)相同的参数，该方程为

$$ \begin{equation}\label{equa_11.77} \dot{x} = -(K_t x + f_t)/ D_t \end{equation} $$

其中 $K_t$ 和 $D_t$ 是切线方向的弹簧和阻尼系数。然后我们就可以算出需要多大的切线力才能防止 $B$ 和 $S$ 之间发生任何滑动。不发生滑动的条件是 $\dot{x} = v$，产生此 $\dot{x}$ 值所需的力是

$$ \begin{equation}\label{equa_11.78} f_{stick} = - K_t x - D_t v \end{equation} $$

现在，我们就可以写出计算库伦摩擦力的规则

$$ \begin{equation}\label{equa_11.79} f_t = \begin{cases} -\mu f_n & \mbox{if } f_{stick} < -\mu f_n \\ \mu f_n & \mbox{if } f_{stick} > \mu f_n \\ f_{stick} & \mbox{otherwise} \end{cases} \end{equation} $$

这里，$\mu$ 是摩擦系数。$f_t$ 被限制在摩擦锥(friction cone)内，这意味着它必须位于 $−\mu f_n$ 到 $\mu f_n$ 的范围内。如果在这个范围内有一个力可以防止 $B$ 和 $S$ 之间的滑动，那么它就是 $f_t$ 的值，否则 $f_t$ 位于最近的范围边界上，并且确实会发生一些滑动。

11.9 扩展阅读 Further Reading

接触和碰撞动力学是一个很大的主题，本章仅提供了简要介绍。从这里开始，接下来比较合理的是阅读 Coutinho (Coutinho, 2001) 和 Brach (Brach, 1991) 的书籍。前者涵盖接触和撞击动力学，而后者专注于撞击。也有一些综述可以看，可以尝试阅读 (Gilardi and Sharf, 2002) 和 (Stewart, 2000) 的评论文章。后者更数学化。另一个适合数学爱好者的项目是 (Pfeiffer and Glocker, 2000) 编辑的讲义。摩擦建模是另一个本章几乎没有涉及的大课题。有关此主题的更多信息，请参阅 Armstrong-Hélouvry et al. (1994), Dupont et al. (2002), Haessig and Friedland (1991)。最后，还可以参考 Lötstedt(1981、1982、1984), Marhefka and Orin (1999), Nakamura and Yamane (2000), Wittenburg (1977), Yamane (2004)。

Chapter11: 接触与碰撞Contact and Impact