1.1. 艺术画廊定理
Art Gallery Theorems
1.1.1. 多边形 (Polygons)
计算几何很多时候都是在处理多边形。真实世界中的很多物体,用多边形来描述会很方便。它不仅可以精确地建模,而且易于计算。它们可以在自动字符识别系统中表示单个字符的形状。 也可以表示机器人需要躲避的物体。图形引擎渲染的实物也可以是由多个多边形碎片来描述。多边形可以很复杂,通常需要将它分割成若干个更简单的部分组成。这就是本章和下一章的主题: 多边形分割。
多边形定义
多边形是平面上由有限条线段围成的区域,这些线段构成了一个简单的封闭曲线。要准确的定义一个简单封闭曲线有些困难。拓扑学会说它是圆形的同胚像(homeomorphic image), 也就是某种变形的圆。这里我们先不谈拓扑,以一种更通俗的方式定义多边形。
令 \(v_0, v_1, v_2, \cdots, v_{n-1}\) 是平面中的 \(n\) 个点。本书中所有的索引都是模 n 的,即\(\mod(n)\),\(v_{n-1}\) 之后的点就是 \(v_0\), 因为 \((n-1)+1 \equiv n \equiv 0 \mod(n)\)。令 \(e_0 = v_0 v_1, e_1 = v_1 v_2, \cdots, e_i = v_i v_{i+1}, \cdots, e_{n-1} = v_{n-1}v_0\)为连接这些点的线段。 当且仅当下述两个条件成立时,我们说这些线段构成了一个多边形:
- 按照循环索引,相邻的一对线段的交点就是它们之间的那个点。即,对于所有的 \(i = 0, \cdots, n-1\) 都有 \(e_i \cap e_{i+1} = v_{i+1}\)。
- 不相邻的线段不相交。即,对所有 \(j \ne i + 1\) 都有 \(e_i \cap e_{j} = \emptyset \)。
这些线段之所以定义了一个曲线(curve),是因为它们端到端的连起来了。这个曲线之所以是封闭的,是因为他们首尾相连形成了一个圈。之所以说这个封闭曲线是简单的,是因为不相邻的线段不相交。
点 \(v_i\) 被称为多边形的顶点(vertex),线段 \(e_i\) 是多边形的边 \(edge\)。一个多边形有 \(n\) 个顶点就有 \(n\) 条边。
在拓扑学里有一个重要的定理 Jordan Curve 定理:
这个定理看起来是显而易见的,似乎不需要什么证明,但实际上要准确的证明它还是挺难的。我们将它看做是理所当然的。平面的这两个部分分别被称为曲线的内部interior和外部exterior。 外部是没有边界的,而内部有边界。这也说明我们把多边形定义成由若干线段围成的区域是合理的。虽然这里我们将多边形 \(P\) 定义为平面上的一个封闭区域,但是有时我们讨论多边形是指它的那些线段。 我们借用拓扑学的符号 \(\partial P\) 来表示 \(P\) 的边界。有 \(\partial P \subseteq P\)。
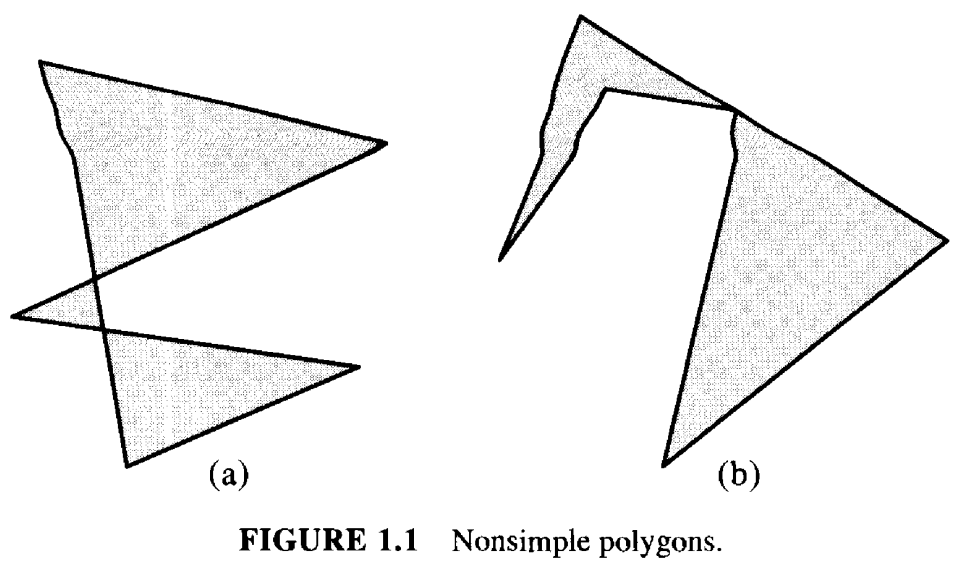
图 1.1 示意了两个非简单多边形 nonsimple polygon。图中的这两个图形,它们都满足上述条件1(相邻的两个线段都有一个公共点), 但是不满足条件2,存在不相邻的线段相交的情况。这样的图形也被称为多边形。而那些满足条件2的多边形被称为简单多边形simple polygon。因为本书中几乎不会出现非简单多边形, 所以我们一般会省略掉这个定语。
按照惯例,我们按照逆时针的方向列出多边形的顶点。这样如果我们按照顶点顺序沿着边界行走,或者说是遍历边界,那么多边形的内部总是在我们的左侧。
1.1.2. 艺术画廊定理 (The Art Gallery Theorem)
问题描述
我们先来研究一下 Klee 提出的一个有趣的问题,它会自然的引出三角剖分,这一最重要的多边形分割问题。设想一个艺术画廊房间可以用 n 个顶点组成的多边形来表示。 Klee 问:需要多少个固定的保安来守卫这个房间?每个保安都被看做一个固定点,他们可以看到所有的方向,可视范围是 \(2 \pi\)。当然,他们不能透视房间的墙壁。 该问题的一个等效表述是,需要多少个点光源才能完全照亮整个房间?在尝试解答之前,我们先形式化的描述一下 Klee 的问题。
可视范围
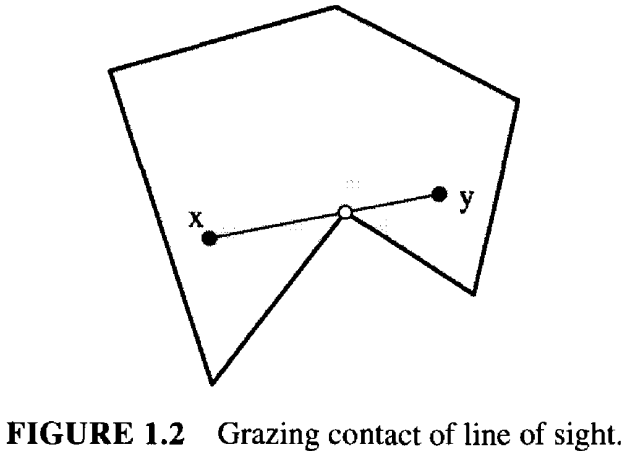
我们先来准确的描述一下可视范围。当且仅当线段 \(xy\)不在多边形 \(P\) 的外部,即 \(xy \subseteq P\),我们说点 \(x\) 可以看到点 \(y\)。 注意这个定义允许视线擦过顶点,就像图 1.2 那样。另一个同样合理的定义是,顶点可以遮挡视线。如果 \(xy \subseteq P\) 并且 \(xy \cap \partial P \subseteq {x, y}\), 则称 \(x\) 可以清晰地看到 \(y\)。我们在练习中偶尔会用到第二个定义(练习 1.1.4[2] 和 [3])。
一个守卫就是一个点。如果多边形中的每个点都能够被一组守卫看到,那么就说这组守卫覆盖cover了该多边形。守卫之间不会彼此遮挡对方的视线。 我们也可以要求守卫只能看到 \(\partial P\) 上的点,因为那里是名画可能出现的位置。这是一个有趣变体,读者可以在练习 1.1.4[1]中探索它。
最大-最小表述
现在,除了“多少”这个短语之外,我们已经将 Klee 的问题的大部分内容形式化了。简而言之,这个问题就是要找出能够覆盖所有\(n\)个顶点的多边形的最小守卫数量的最大值。 这种“最大-最小max-over-min”表述对于新手来说可能比较难懂,但它在数学中却非常常用,所以我们会花些时间仔细解释。
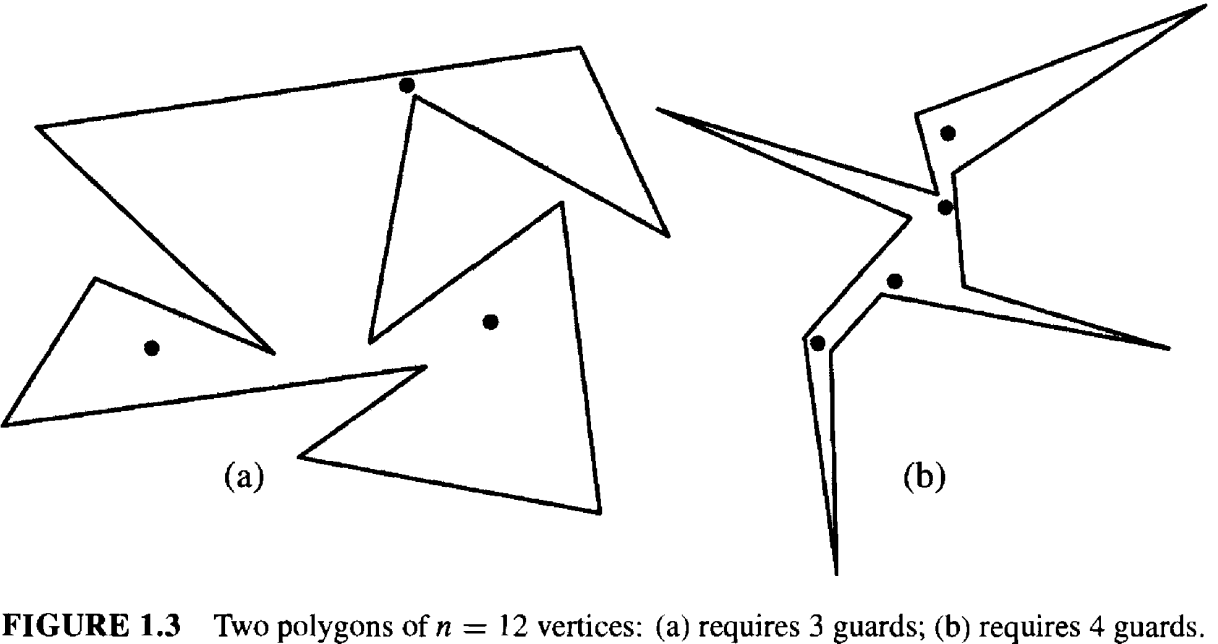
对于任意给定的多边形,一定存在可以覆盖该多边形的最小数量的守卫。图 1.3(a) 中的 12 个顶点的多边形显然显然需要三个守卫来覆盖,尽管这三个守卫的位置有相当大的自由度。 但是,对于所有可能的 12 个顶点的多边形,三个守卫就是所需的最大数量吗?不是的。如图 1.3(b) 中的多边形,同样有 12 个顶点,却需要四个守卫。 任何 12 个顶点的多边形最多需要多少个守卫?我们最终会证明,对于任何 12 个顶点的多边形,四个守卫总是足够的。这就是 Klee 问题所寻求的答案: 用一个关于 \(n\) 的函数来表示足以覆盖任何 \(n\) 个顶点的多边形的最小守卫数量。这个数量的守卫被称为覆盖的必要和充分条件。 必要条件是指某些多边形至少需要那么多守卫,而充分条件是指对于任何多边形那么多守卫总是足够的。
在进一步探讨之前,我们先将问题形式化。设 \(g(P)\) 为覆盖多边形 \(P\) 所需的最小守卫数量,\(g(P) = \min_s |\{S: S 覆盖 P\}|\)。 其中 \(S\) 是个点集,\(|S|\) 是集合\(S\)的大小,即其中元素的数量。设 \(P_n\) 为一 \(n\) 个顶点的多边形。\(G(n)\) 是函数 \(g(P_n)\) 的最大值:\(G(n) = \max_{P_n} g(P_n)\)。 Klee 的问题是要确定函数 \(G(n)\)。我们可能找不到直接的证据,说明对与每个 \(n\) 都有 \(G(n)\) 的定义。对于某些多边形,是否有限数量的守卫不足够覆盖它。 幸运的是,\(G(n)\) 对所有 \(n\) 都是有限的,这点我们后面会解释。但它是否可以表示为一个简单的公式,或者必须用一个无限的映射表来记录,则不太清楚。
实验探索
\(n\) 的充分性 Sufficiency of n。 显然,至少需要一名警卫。这给出了 \(G(n)\) 的下限 \(1 ≤ G(n)\)。对于任何多边形,\(n\) 名警卫就足够了。 在每个顶点安排一名警卫,肯定能覆盖整个多边形。这给出了 \(G(n)\)的上限 \(G(n) ≤ n\)。但 \(n\) 个守卫是否足够,还需要证明。事实上它是正确的,很符合我们的直觉。 但在三维空间中它就失效了,因为在多面体的每个顶点放置守卫并不一定能覆盖整个多面体(参见练习 1.1.4[6])。
有很多类似艺术画廊的问题。大多数时候求解它们的最简单方法就是,先找到一些通用的例子来确定 \(G(n)\) 的下界,证明有时需要大量的警卫。 当看起来无论多么巧妙的手段,都无法增加所需的警卫数量时,就该转向证明这个数量也是足够的了。我们将按如下方式进行。
小 \(n\) 的必要性 Necessity for Small n。 当 \(n\) 较小时,稍加探索就能猜出 \(G(n)\) 的值。显然,每个三角形只需要一个守卫,因此 \(G(3) = 1\)。
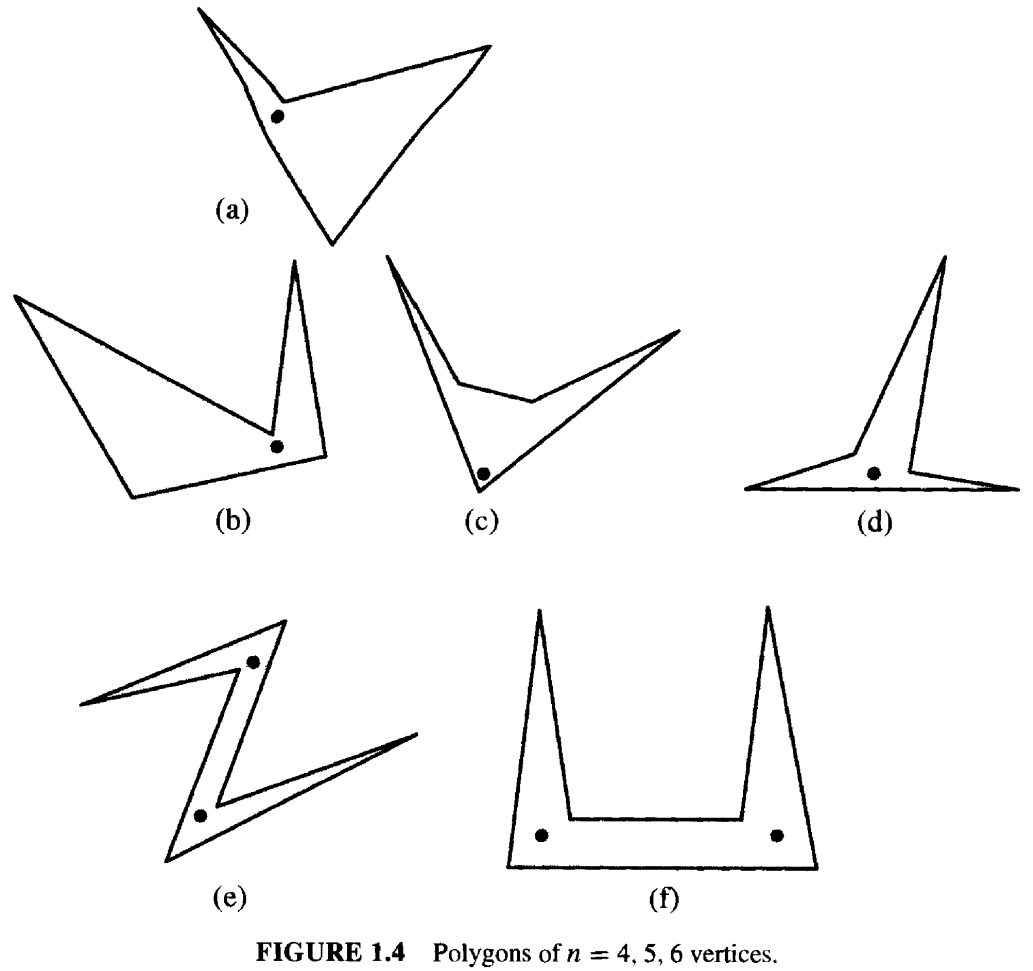
四边形可分为两类,凸四边形和具有凹顶点(reflex vertex)的四边形。直观地讲,如果一个多边形没有凹顶点,那么它就是凸的。 这个重要概念将在第三章详细探讨。 如果一个顶点的内角严格大于\(\pi\),则称该顶点为反射(reflex)顶点,凹的。否则被称为凸(convex)的。凸四边形有四个凸顶点。 一个四边形最多只能有一个凹顶点,其原因将在1.2节中阐明。如图1.4(a)所示,即使是具有凹顶点的四边形,也可以被放置在该顶点附近的单个守卫覆盖。因此 \(G(4) = 1\)。
对于五边形来说,情况就复杂一点了。当然,凸五边形只需要一个守卫,而只有一个凹顶点的五边形也只需要一个守卫,原因与四边形相同。五边形可以有两个凹顶点。 它们可以相邻,也可以被一个凸顶点隔开,如图 1.4(c) 和 (d) 所示。在两种情况下,一个守卫就足够了。因此,\(G(5) = 1\)。
六边形可能需要两名守卫,如图 1.4(e) 和 (t) 所示。稍加实验就能确定,最多只需要两名守卫,因此 \(G(6) = 2\)。
至少需要 \(\lfloor n/ 3 \rfloor\)
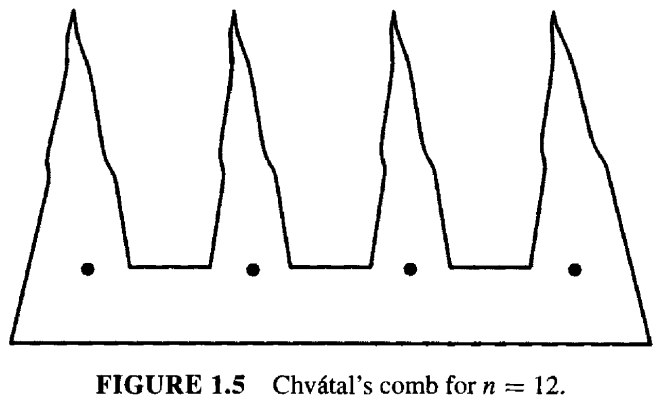
此时,读者或许能够直接跳到图 1.4(f) 对更大的 \(n\) 值进行推广。图 1.5 设计了一个 n = 12 的多边形,注意它与图 1.4(t) 有些相似。 这个“梳子”形状的多变相由 \(k\) 个叉齿组成,每个叉齿有两条边,相邻的叉齿之间由一条边隔开。将每个叉齿与其右侧的分隔边关联成一组,最右侧的叉齿与底边关联, 我们得到一个由 \(k\) 个叉齿组成的梳子,它有 \(n = 3k\) 条边和顶点。由于每个叉齿都需要自己的守卫,因此通过这个例子证明,当 \(n = 3k\) 时,\(n/3 ≤ G(n)\)。 这就是我之前所说的,一个通用的例子可以用来确定 \(G(n)\) 的下界。
注意到 \(G(3) = G(4) = G(5)\) 可能会让人猜想 \(G(n) = \lfloor n/3 \rfloor\),而事实上这个猜想是正确的。 这正是解决此类问题的常用数学方法。首先,通过实验探索推测答案,得出一个可能的结果,最终证明它。现在我们来证明它。
1.1.3 Fisk 的充分性证明(Fisk's Proof of Sufficiency)
第一个证明 \(G(n) = \lfloor n / 3 \rfloor\) 的是 Chvátal (1975)。他的证明采用了归纳法,假设对于所有 \(n < N\) 的情况,都需要\(\lfloor n/3 \rfloor\)的守卫, 他通过小心地移除多边形的一部分以减少其顶点数,应用归纳假设,然后重新连接移除的部分,证明了 \(n = N\) 时仍然成立。该证明穷举了多种情况,相当复杂。
三年后,Fisk 找到了一个非常简单的证明,只占了期刊的一页(Fisk 1978)。我们将在这里展示 Fisk 的证明。
对角线和三角分割
Fisk 的证明的关键在于将多边形按照对角线划分成若干个三角形。多边形\(P\)的对角线是其两个顶点 \(a,b\) 之间的线段,这两个顶点彼此能够清晰的看到对方。 这意味着闭线段(closed segment) \(ab\) 与 \(\partial P\) 的交集就是 \(\{a,b\}\)。或者说从\(a\)到\(b\)的开线段(open segment)与 \(\partial P\)不相交。 因此对角线不能与边界擦过。
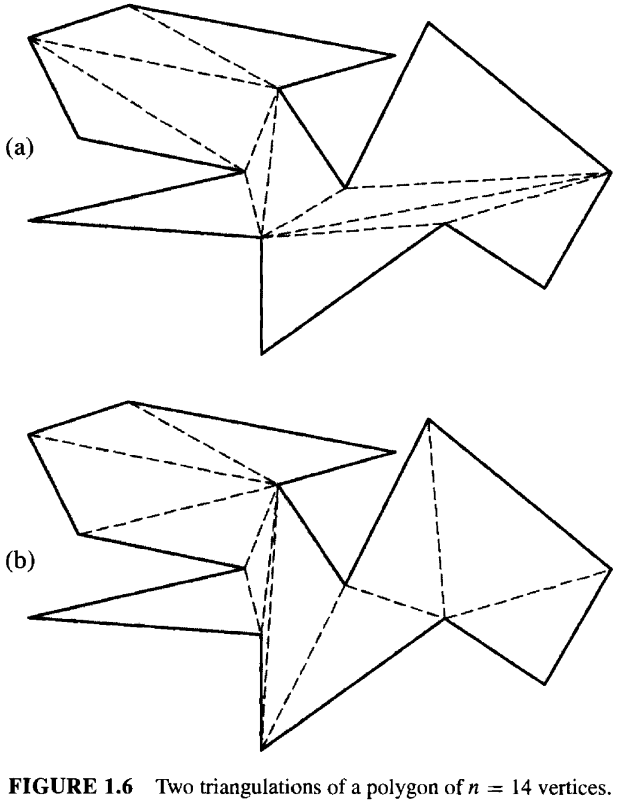
如果两个对角线的交点是他们的端点的子集,那么我们成这两个对角线不相交,即,它们没有相同的内点。如果我们在多边形中添加尽可能多的不相交对角线, 那么多边形内部将被划分为若干个三角形。这种多边形的分割方法被称为三角分割triangulation。只要满足对角线的定义和不相交的条件,我们可以随意添加对角线。 通常一个给定的多边形可以有多种三角分割的方法。图 1.6 中给出了一个 \(n=14\) 的多边形的两种三角分割。
我们把每个多边形都可以三角分割的证明推迟到 1.2 节,现在我们只假设三角分割的存在。
三着色 3-coloring
假设给定一个任意的 \(n\) 个顶点的多边形 P。Fisk 证明的第一步是对 \(P\) 进行三角分割。第二步是"回想recall"得到的图可能是三色图。 我们需要解释这个图是什么,以及三色图的含义。
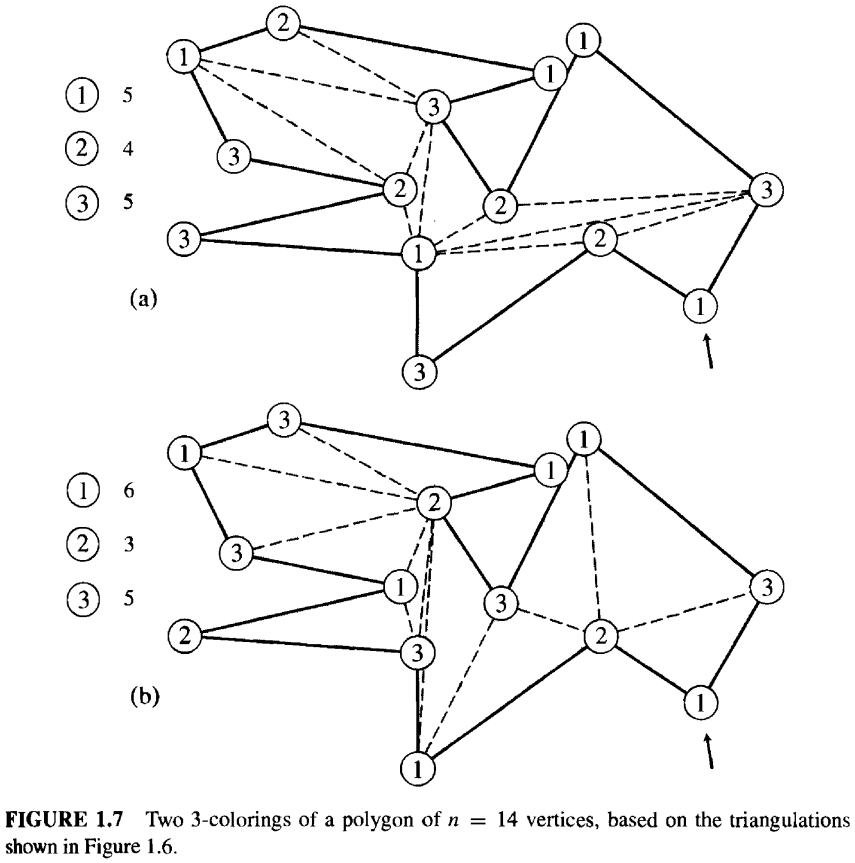
令 \(G\) 为与三角分割相关联的图,它的弧是多边形的边和三角分割的对角线,其节点是多边形的顶点。这是 Fisk 使用的图。 图的 k-coloring 是将 \(k\) 种颜色分配给图的节点,使得由弧连接的任何两个节点都不会被分配相同的颜色。 Fisk 声称每个三角分割图都可以是 3 色的。我们将再次推迟对这一说法的证明,但只需进行一些实验说明它是合理的。图 1.6 中的三角分割的三着色如图 1.7 所示。 从箭头所指的顶点开始,用三种颜色任意为其着色,其余节点的颜色也就随之确定了,因为没有多余的选择。 粗略地说,这种方法总是成立的,因为强制选择永远不会回到先前的选择。而这种情况从未发生的原因在于底层图形是一个多边形(根据定义,没有孔)。
Fisk 证明的第三步是,在相同颜色的顶点放置守卫就可以保证多边形的可见性覆盖。他的推理如下。 假设使用红色、绿色、蓝色进行三着色。每个三角形都必须是这三种颜色各一种。因此,每个三角形都有一个角是红色的。 假设在每个红色节点上都放置了守卫,那么每个三角形都有一个角上站了一个守卫。显然,这个三角形被该守卫覆盖了。因此每个三角形都被覆盖。 最后,三角分割中的三角形集合完全覆盖了多边形。因此,如果在红色节点上放置守卫,则整个多边形都被覆盖了。 同样,如果在绿色节点或蓝色节点上放置守卫,则整个多边形都被覆盖了。
Fisk 证明的第四步也是最后一步应用了"鸽笼原理pigeon-hole principle",如果将 \(n\) 个物体放入 \(k\) 个鸽笼中, 则至少有一个鸽笼的物体数量不超过 \(n/k\) 个。因为如果每个鸽笼的物体数量超过 \(n/k\) 个,则物体总数将超过 \(n\)。 在这里,\(n\) 个物体代表三角分割图的 \(n\) 个节点,\(k\) 个鸽笼代表 3 种颜色。该原理决定了,同一种颜色的使用次数不会超过 \(n/3\) 次。 由于 \(n\) 是整数,我们可以得出一种颜色的使用次数不超过 \(\lfloor n/3 \rfloor\) 次。现在,我们得到了充分性证明, 只需在 3 着色中使用频率最低的颜色的节点处放置守卫,就可以确保,将用不超过 \(G(n) = \lfloor n/3 \rfloor\) 种颜色覆盖整个多边形。
如果您不能从这个过程中感受到优美(或至少不迷人),那么您就不会从这本书中获得太多乐趣!
在图 1.7 中,\(n = 14\),因此 \(\lfloor n/3 \rfloor = 4\)。图 (a) 中使用了四次颜色2。在 (b) 中仅使用了三次颜色2。这说明三着色理论并不总是能够找到最优的守卫方案。
1.1.4 练习
- 守护墙壁Guarding the walls。构造一个多边形 \(P\) 并布置一些守卫,使得守卫能够看到 \(\partial P\) 上的每个点,但至少有一个 \(P\) 内部的点不被任何守卫看到。
- 清晰可视,点守卫clear visibility, points guards。Klee 问题中关于清晰可见clear visibility的答案是什么(见1.1.2节)?
更具体地说,设 \(G'(n)\) 是足以清晰看到 \(n\) 个顶点的多边形中的每个点的最小守卫数量。守卫可能出现在 \(P\) 中任何点上,这与只能站在顶点的顶点守卫vertex guards不同。
Are clearly seeing guards stronger or weaker than usual guards? What relationship between \(G'(n)\) and \(G(n)\) follows from their relative stength? (\(G(n)\) 的定义见 1.1.2 节) Fisk 的证明是否满足 \(\lfloor n /3 \rfloor\) 对于清晰可见来说是否充分? 请尝试精确计算 \(G'(n)\)。 - 清晰可视,定点守卫clear visibility, vertex guards(Thomas Shermer)。与问题2一样。只是守卫被固定在顶点上。
- [open]边缘守卫Edge guards。边缘守卫是指可能巡逻多边形一条边 \(e\) 的守卫。如果存在点 \(x \in e\) 并且 \(x\) 可以看到 \(y \in P\),那么我们说点 \(y\) 被该守卫覆盖了。
或者说我们把边 \(e\) 想象成一个荧光棒。\(P\) 中被该荧光棒照亮的部分就是边缘守卫覆盖的点集。
Toussaint 证明了 \(\lfloor n/4 \rfloor\) 的边缘守卫有时是必要的,如图 1.8 所示 "half-swastika"多边形(O'Rourke 1987,p. 83)。他推测,除了少数较小的 \(n\) 值外, \(\lfloor n/4 \rfloor\) 足够。这个奇怪的例外是由图 1.9 所示的两个"arrowhead"多边形所致,而这两个多边形似乎并不具有普遍性。这些例子取自 Shermer (1992)。
请证明 Toussaint 的猜想正确或者错误。
- [open]星形多边形的边缘守卫Edge guards in star polygons。星形多边形是指可被单个(点)守卫覆盖的多边形。 Toussaint 证明了 \(\lfloor n/5 \rfloor\) 的边守卫有时是必须的。如图 1.10 所示(O' Rourke 1987,p. 119 页)。 \(\lfloor n/5 \rfloor\) 的充分性的猜想已被证明在 \(n = 14\) 时是错误的(Subramaniyam & Diwan 1991),但除此之外,其他方面知之甚少。 请证明,对于某个常数 \(c > O\),\(\lfloor n/5 + c \rfloor\)是否足够。
- 多面体中的守卫Guards in polyhedra。设计一个多面体,使得在每个顶点放置一个守卫,都无法完全覆盖其内部。 多面体是多边形的三维版本,由多边形面组成,并包围一个三维空间。第四章(4.1节)将提供精确的定义。提示:参见O'Rourke(1987,Sec. 10.2.2)。