1.2 三角分割理论
(Triangulation: Theory)

本节我们将证明每个多边形都可以进行三角分割，还会介绍一些三角分割的基本性质。在后面的章节(1.4-1.6.5)中，我们将讨论三角分割的算法。

当被问到"每个多边形都一定能被三角分割吗?这个问题时，人们会自然想到另一个问题"多边形怎么可能不能分割成三角形呢?"确实没有一个不能的。但如果你觉得这个问题太显而易见，无需证明，这个问题的三维版本: 这个命题直接推广到三维空间中是错误的! 参见 O'Rourke(1987,p.253-4)。

1.2.1 对角线的存在性(Existence of a Diagonal)

证明三角分割存在的关键是证明对角线的存在。一旦证明，剩下的就很容易了。为此，我们需要另一个更显而易见的事实: 每个多边形至少有一个严格的凸顶点。

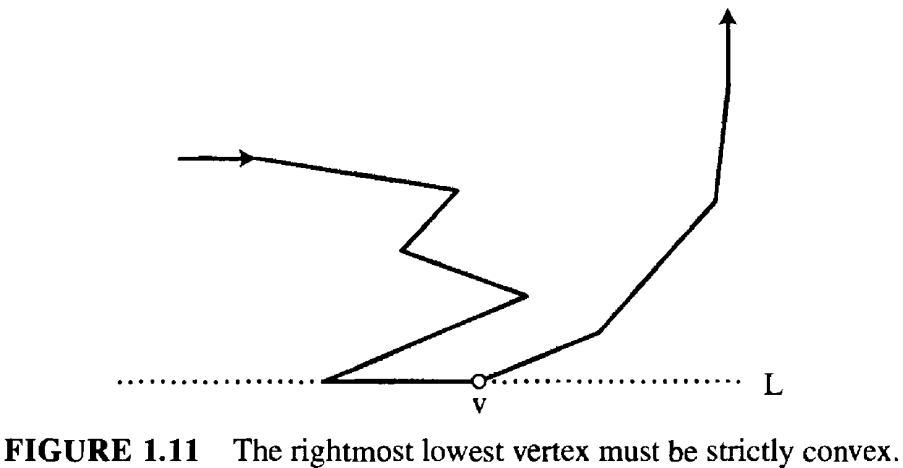
引理 1.2.1. 每个多边形必须至少有一个严格的凸顶点(strictly convex vertex)。

证明：如果我们沿着多边形的边逆时针走，遇到严格的凸顶点就需要左转，而凹顶点就要右转。行走的过程中，多边形的内部始终在我们的左侧。

设 \(L\) 为通过 \(P\) 的最低顶点 \(v\) 的直线，点 \(v\) 是多边形的所有顶点中 y 坐标最小的那个; 如果有多个最低顶点，那么 \(v\) 取其中最右侧的顶点。如图1.11所示。

\(P\)的内部一定在 \(L\)上方。从 \(v\) 出发指向下一个点的边必定也位于 \(L\) 上方。这些条件决定了，我们在 \(v\) 处一定左转，因此 \(v\) 就是严格凸顶点。□

这个证明可以用来测试多边形的方向(练习 1.3.9[3])。

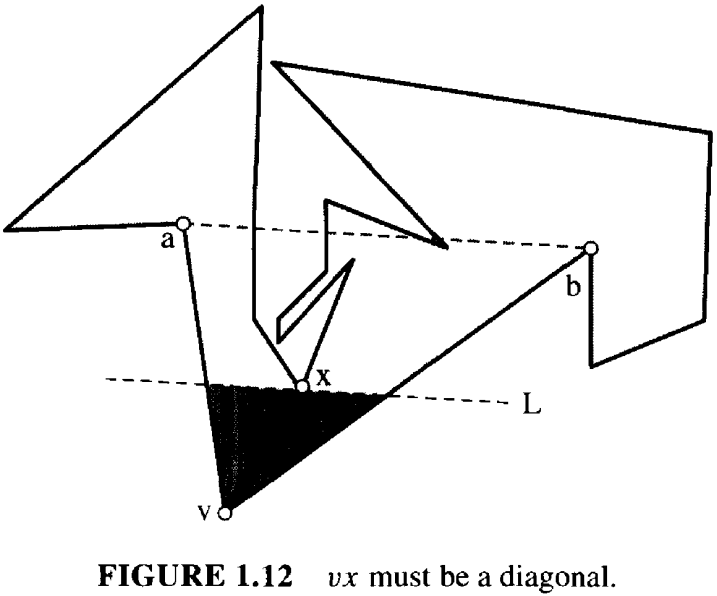
引理 1.2.2 (Meisters). 每个顶点数 \(n ≥ 4\) 的多边形都有一条对角线。

证明：设 \(v\) 是一个严格凸顶点，其存在性由引理 1.2.1 保证。\(a\) 和 \(b\) 分别是 \(v\) 前后两个顶点。

如果 \(ab\) 是对角线，则讨论结束。

假设 \(ab\) 不是对角线。则 \(ab\) 要么在 \(P\) 的外部，要么与 \(\partial P\) 相交。无论哪种情况，由于 \(n > 3\)，那么闭合三角形 \(\Delta avb\) 至少包含一个除 \(a, v, b\) 之外的顶点。

设 \(x\) 为 \(\Delta avb\) 中距离 \(v\) 最近的顶点，距离可以通过垂直于 \(ab\) 的直线来判断。如果我们用一条平行于 \(ab\) 的直线从 \(v\) 向 \(ab\) 平移，\(x\) 将是遇到的第一个顶点。如图 1.12 所示。

现在我们说 \(vx\) 是 \(P\) 的一条对角线。因为，显然 \(\Delta avb\) 的内部与 \(v\) 和 \(L\) 所围成的区域相交(图中阴影区域)，其中没有 \(\partial P\) 的点。因此，\(vx\) 除了在 \(v\) 和 \(x\) 相交之外，不可能与 \(\partial P\)相交，所以它是一条对角线。□

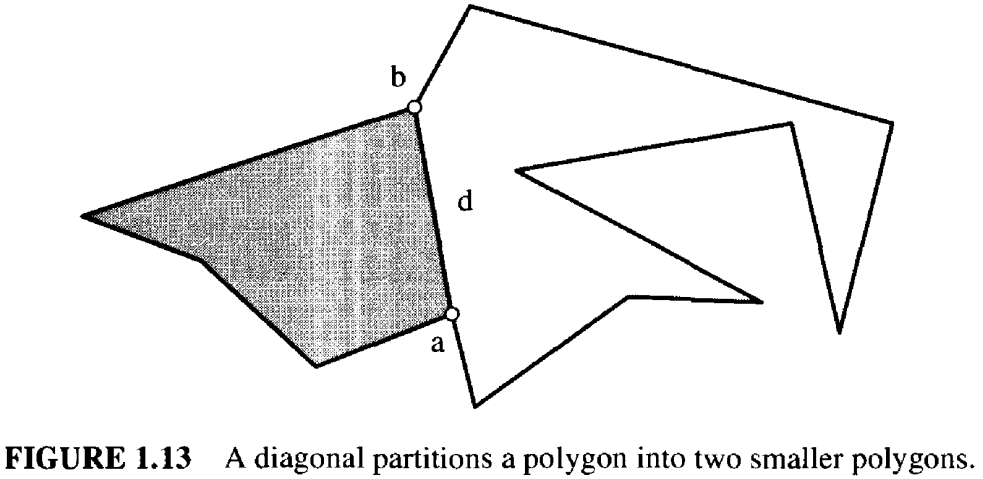
定理 1.2.3 (Triangulation). 每个有 \(n\) 个顶点的多边形，都可以通过添加零个或者多个对角线，分割成若干三角形。

证明：采用数学归纳法证明。若 \(n = 3\)，多边形就是一个三角形，命题成立。

\(n ≥ 4\) 时，根据引理 1.2.2 多边形 \(P\) 一定存在一条对角线，记为 \(d = ab\)。根据对角线的定义，\(d\) 与 \(\partial P\) 的交点就是它的两个端点。它将 \(P\) 分割成了两个多边形。这两个多边形都以 \(d\) 为边，并且顶点数都少于 \(n\)。如图 1.13 所示。

整个过程并没有增加顶点，并且分割出来的两个多边形，各自除了顶点 \(a,b\) 之外，至少有一个顶点不属于对方。所以分割出来的两个多边形的顶点数量变少了。我们再对分割出来的两个多边形递归下去，就可以证明该定理。□

1.2.2 三角分割的特性(Properties of a Triangulations)

一般来说，一个多边形可以有很多种不同的三角分割方法(练习 1.2.5[4])，但它们都有相同数量的对角线和三角形，这可以通过与定理 1.2.3 中相同的论证方法证明。

引理 1.2.4 (对角线的数量). 具有 \(n\) 个顶点的多边形 \(P\) 的每个三角分割，都需要使用 \(n - 3\) 条对角线，分割成 \(n - 2\) 个三角形。

证明：仍然采用数学归纳法证明。对于 \(n = 3\) 的情况，命题显然成立。

当 \(n ≥ 4\) 时，对角线 \(d = ab\) 将 \(P\) 分割成两个多边形 \(P_1, P_2\)。假设这两个多边形分别有 \(n_1, n_2\) 个顶点。我们有 \(n_1 + n_2 = n + 2\)，因为 \(a,b\) 在 \(n_1, n_2\) 里被计数了两次。

将假设应用于这两个多边形，我们有 \((n_1 - 3) + (n_2 -3) + 1 = n -3\) 个对角线，最后的 \(+1\) 项是对 \(d\) 的计数。并且有 \(n_1 - 2) + (n_2 - 2) = n - 2\) 个三角形。□

推论 1.2.5 (内角和). \(n\) 个顶点的多边形内角和为 \((n-2)\pi\)。

证明：根据引理 1.2.4，多边形可以分割成 \(n-2\) 个三角形，每个三角形的内角和是 \(\pi\)，所以多边形的内角和是 \((n-2)\pi\)。□

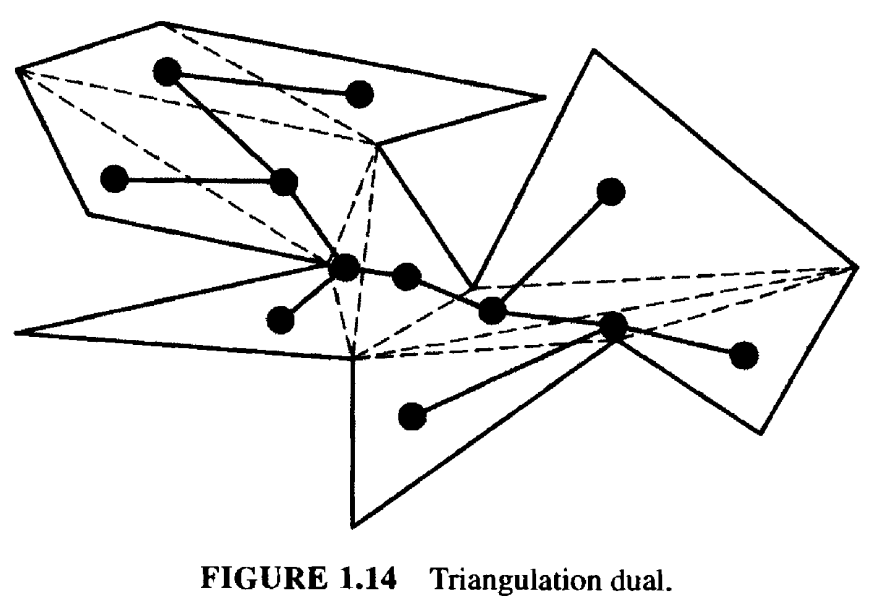
1.2.3 三角分割的对偶(Triangulations Dual)

图论中有一个重要概念，就是图的"对偶dual"。我们不需要完全理解这个概念，有时会根据需要构建对偶图。研究三角分割的对偶图可以揭示三角分割中的有用结构。

如图 1.14 所示，在多边形三角分割的对偶图 \(T\) 中，每个节点对应一个三角形，如果两个三角形共享一条对角线，那么这两个节点之间就有一条边连接。

引理 1.2.6. 三角分割的对偶图是一颗树，并且每个节点的度最大为 3。

证明：每个节点的度最大为三，是因为三角形最多有三条边可共享。

假设 \(T\) 不是一棵树。那么它必然存在一个环路 \(C\)。如果将此环路在平面上用路径 \(\pi\) 圈出来。具体的，我们可以用直线段连接构成 \(C\) 的三角形的共享对角线的中点，那么 \(\pi\) 必然包含一些多边形顶点：即 \(\pi\) 与每条对角线的一个端点相交namely one endpoint of each diagonal crossed by \(\pi\)。但 \(\pi\) 也必然包含多边形外部的点，因为这些被包含的顶点位于 \(\partial P\) 上。这与多边形的简单性相矛盾。□

\(T\) 的叶子节点的度为一。nodes of degree two lie on paths of the tree. 大体意思是非叶子节点，不分叉的节点的度是2。分叉的节点度是3。注意，当以任意一个度数为1或者2的节点为 \(T\) 的根节点时，它就是一棵二叉树！二叉树在计算机科学中十分常见，三角分割对偶和二叉树之间的这种对应关系，经常被用来解决一些问题(练习1.2.5[7])。

通过引理 1.2.6 证明 Meisters 的"双耳定理Two Ears Theorem"，这个定理虽然很简单，但是非常实用。对于多边形上连续的三个顶点 \(a,b,c\)，如果 \(ac\) 是多边形的一个对角线，那么这三个顶点就构成了多边形的一个耳朵，顶点 \(b\) 就是耳朵尖。如果两个耳朵内部不相交，就称这两个耳朵不重叠nonoverlapping。

定理 1.2.7 (Meisters 的双耳定理). 每个顶点数 \(n ≥ 4\) 的多边形，都至少有两个耳朵。

证明：三角分割对偶树中的一个叶节点对应一只耳朵。而一棵包含两个或多个节点的树必须至少有两片叶子。根据引理 1.2.4，如果多边形的顶点数 \(n ≥ 4\)，那么它的三角分割对偶树就有 \((n - 2) ≥ 2\) 个节点。□

1.2.4 三着色证明(3-Coloring Proof)

双耳定理可以很容易地证明三角分割图的三色性3-colorability。其思路是移除一个耳朵用于指引着色，因为一个耳朵与一条对角线相交，所以可以一致地consistently着色。

定理 1.2.8 (三着色).一个多边形 \(P\) 的三角分割图可以被三着色。

证明：仍然采用数学归纳法证明。显然，一个三角形是可以三着色的。

当 \(n ≥ 4\) 时。根据定理 1.2.7，\(P\) 中一定有一只耳朵 \(abc\)，耳尖为 \(b\)。如果切掉这只耳朵，可以得到一个新的多边形 \(P'\)。这相当于，用 \(\partial P'\) 中的边 \(ac\) 替换 \(\partial P\) 中的序列 \(abc\)。\(P'\) 有 \(n - 1\) 个顶点，它缺少顶点 \(b\)。

假设当 \(n ≥ 4\) 时，命题对于有 \(n-1\) 个顶点的 \(P'\) 成立。现在将耳朵放回原处，用顶点 \(a\) 和 \(c\) 未使用的颜色为 \(b\) 着色。就实现了多边形 \(P\) 的三着色。□

1.2.5 练习