1.3 多边形的面积
(Area of Polygon)

本节我们将要研究如何计算一个多边形的面积。虽然这个问题本身就很有趣，但是我们的目标是为计算半平面的包含关系、线段的交点、可见性关系做一些准备工作，为最终在 1.6.5 节中引出三角分割算法打基础。

1.3.1 三角形的面积(Area of Triangle)

三角形的面积就是底乘以高除以二。但是如果我们想要计算一个任意顶点 $a,b,c$ 的三角形 $T$ 的面积，这个公式并不好用。我们把它的面积记为 $\mathcal{A}(T)$。底很容易计算，就是 $|a - b|$，但我们并不能直接从坐标中写出三角形的高，除非三角形有一条边恰好与某个坐标轴平行。

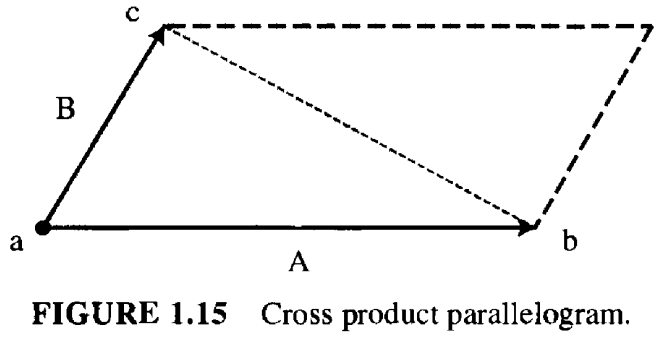
1.3.2 叉乘(Cross Product)

根据现行代数，我们知道两个向量的叉乘的模长就是他们确定的平行四边形的面积。如果 $A,B$ 是两个向量，那么 $|A\times B|$ 就是以 $A,B$ 为边的平行四边形的面积。如图 1.15 所示。因为任何三角形都可以看做是一个平行四边形的一半，这就可以直接写出，根据顶点坐标计算三角形面积的公式。只需要计算 $A = b - a$, $B = c - a$，那么它的面积就是 $A \times B$ 模长的一半。这个叉乘可以通过行列式计算得出，其中 $\hat{i}, \hat{j}, \hat{k}$ 分别是沿$x,y,z$方向的单位向量。 $$ \begin{equation}\label{f1.1} \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ A_0 & A_1 & A_2 \\ B_0 & B_1 & B_2 \end{vmatrix} = (A_1B_2 - A_2B_1)\hat{i} + (A_2B_0 - A_0B_2)\hat{j} + (A_0B_1 - A_1B_0)\hat{k} \end{equation} $$ 对于二维的向量，$A_2 = B_2 = 0$，所以上式可以简化成 $(A_0B_1 - A_1B_0)\hat{k}$。叉乘得到的向量垂直于三角形的平面。三角形的面积就是: $$ \mathcal{A}(T) = \frac{1}{2}(A_0B_1 - A_1B_0) $$ 将 $A = b - a$ 和 $B = c -a$ 带入上式有 $$ \begin{align}\label{f1.2} 2\mathcal{A}(T) & = a_0b_1 - a_1b_0 + a_1c_0 - a_0c_1 + b_0c_1 - c_0b_1 \\ & = (b_0 - a_0)(c_1 - a_1) - (c_0 - a_0)(b_1 - a_1) \end{align} $$ 如此，我们就得到了一个以三角形顶点坐标计算三角形面积的公式。

1.3.3 行列式(Determinant Form)

还有另一种表示叉乘计算的方法，虽然其形式相同，但更容易推广到更高维空间。注意，叉乘运算仅限于三维向量(或第三坐标为零的二维向量)。更准确地说，叉乘得到的并不是另一个向量，而是一个二重向量bivector的外积。

上面得到的表达式($\ref{f1.2}$)是三个点坐标的 $3 \times 3$ 行列式的值，其中第三个坐标替换为 1: $$ \begin{equation}\label{f1.4} \begin{vmatrix} a_0 & a_1 & 1 \\ b_0 & b_1 & 1 \\ c_0 & c_1 & 1 \end{vmatrix} = (b_0 - a_0)(c_1 - a_1) - (c_0 - a_0)(b_1 - a_1) = 2\mathcal{A}(T) \end{equation} $$ 练习 1.6.8[1] 将探讨这个行列式，这里我们将它规结为一个引理.

引理 1.3.1. 三角形 $T = (a,b,c)$ 的面积两倍由下式给出: $$ \begin{equation}\label{f1.5} 2\mathcal{A}(T) = \begin{vmatrix} a_0 & a_1 & 1 \\ b_0 & b_1 & 1 \\ c_0 & c_1 & 1 \end{vmatrix} = (b_0 - a_0)(c_1 - a_1) - (c_0 - a_0)(b_1 - a_1) \end{equation} $$

1.3.4 凸多边形的面积(Area of a Convex Polygon)

既然我们有了三角形面积的表达式，那么就很容易计算任何多边形的面积，只需先进行三角分割，然后对三角形面积求和即可。但如果能避免三角分割这个相对复杂的步骤就更好了，而且这确实是可行的。在讨论这个问题之前，我们先考虑三角分割简单的凸多边形。

每个凸多边形都可以三角化成一个扇面，所有的对角线都指向一个共同的顶点。任何一个顶点都可以用作扇面的中心，如图 1.16 所示。因此一个多边形的顶点按照逆时针标记为 $v_0, v_1, \cdots, v_{n-1}$，它的面积可以通过下式计算。其中 $v_0$ 是扇面中心。 $$ \begin{equation}\label{f1.6} \mathcal{A}(P) = \mathcal{A}(v_0, v_1, v2) + \mathcal{A}(v_0, v_2, v_3) + \cdots + \mathcal{A}(v_0, v_{n-2}, v_{n-1}) \end{equation} $$

接下来我们先研究凸四边形和非凸四边形，为后面证明定理 1.3.3 作些热身。凸四边形与非凸四边形的相对关系是显而易见的。

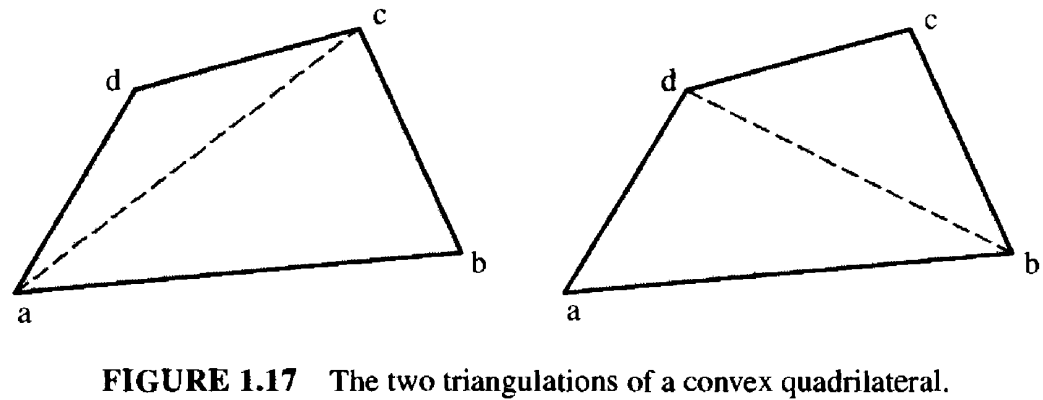
1.3.5 凸四边形的面积(Area of a Convex Quadrilateral)

一个凸四边形 $Q = (a,b,c,d)$ 可能有两种不同的三角化方法，如图 1.7 所示，所以它的面积可以按照如下的方式计算： $$ \mathcal{A}(Q) = \mathcal{A}(a,b,c) + \mathcal{A}(a,c,d) = \mathcal{A}(d,a,b) + \mathcal{A}(d, b,c) $$ 对第一种三角化方法，套用式 ($\ref{f1.2}$) 有 $$ \begin{array}{lr} 2\mathcal{A}(Q) & = a_0b_1 - a_1b_0 + a_1c_0 - a_0c_1 + b_0c_1 - c_0b_1 \\ & + a_0c_1 - a_1c_0 + a_1d_0 - a_0d_1 + c_0d_1 - d_0c_1 \end{array} $$ 其中，$a_1c_0 - a_0c_1$出现在 $\mathcal{A}(a,b,c)$ 和 $\mathcal{A}(a,c,d)$ 并且符号相反，所以可以约去这两项。因此关于对角线 $ac$ 的项就约去了。类似的，对于第二种三角化方法，对角线 $bd$ 相关的项也可以约去。因此，我们就得到了一个与三角分割无关的面积表达式，这正是我们想要的。

推而广之，我们发现多边形的每条边都有两项，而内部的对角线则没有。所以如果顶点 $v_i$ 的坐标为 $x_i, y_i$，那么凸多边形的面积的两倍可以由下式得到: $$ \begin{equation}\label{f1.9} 2\mathcal{A}(P) = \Sigma_{i=0}^{n-1} \left(x_i y_{i+1} - y_ix_{i+1} \right) \end{equation} $$ 我将会看到该式对于非凸多边形也成立。

1.3.6 非凸四边形的面积(Area of a Nonconvex Quadrilateral)

现在，假设我们有一个如图 1.18 所示的非凸四边形 $Q = (a,b,c,d)$。它只有一种三角分割的方法，使用对角线 $db$。我们刚刚看到面积的公式与对角线的选择无关，所以它应当仍然满足公式，尽管连线 $ac$ 在多边形 $Q$ 的外面。 $$ \mathcal{A}(Q) = \mathcal{A}(a,b,c) + \mathcal{A}(a,c,d) $$ 这个公式有一个直观的解释，$\mathcal{A}(a,c,d)$ 是一个负数，相当于从三角形 $\Delta abc$ 中减去它所围成的面积。事实上，注意到 $a,c,d$ 是一个顺时针的路径，所以它对应的叉乘结果就是负数。

非凸四边形所观察到的这种现象是普遍的，正如我们将要展示的证明那样。

1.3.7 任意中心的面积(Area from an Arbitrary Center)

现在我们对前面的案例分析做一些形式化的表述，最终将用于求取一般非凸多边形的面积。我们先把对在三角分割的面积求和的方法，推广到基于任意点 $p$ 的面积求和，这个点可能是多边形外的一个点。设 $T = \Delta abc$ 为一个顶点按逆时针方向排列的三角形，$p$ 为平面上的任意一点。则有:

$$ \mathcal{A}(T) = \mathcal{A}(p,a,b) + \mathcal{A}(p,b,c) + \mathcal{A}(p, c, a) $$

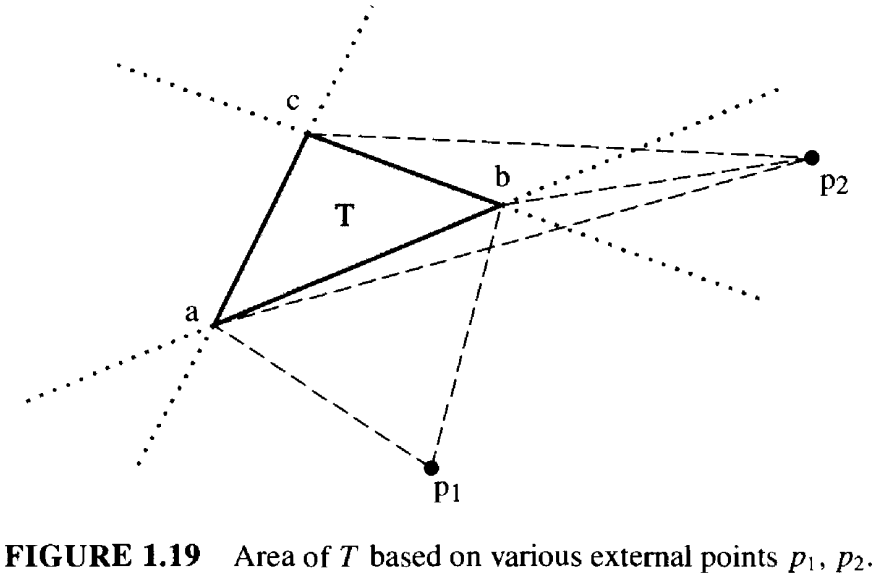
如图 1.19 所示，取点 $p = p_1$，那么上式的第一项 $\mathcal{A}(p_1, a, b)$ 就是一个负数，因为它的顶点时顺时针排列的。而另外两项则都是正数，因为它们的顶点顺序是逆时针的。注意，负数的 $\mathcal{A}(p_1, a, b)$ 的几何意义就是，从四边形 $(p_1, b, c, a)$ 中减去三角形 $T$ 之外的面积，所以这三项求和得到的恰好就是 $\mathcal{A}(T)$。

类似的从 $p_2$ 出发，即 $p = p_2$，$\mathcal{A}(p_2, a, b)$ 和 $\mathcal{A}(p_2, b, c)$ 都是负的，因为他们的顶点都是顺时针排列的，所以需要将它们从 $\mathcal{A}(p_2, c, a)$ 中移除，而这一项是个正数，所得到的恰好就是面积 $\mathcal{A}(T)$。

平面上除 $T$ 内部以外，$p$ 在其它任何位置上，都可以规结为 $p_1, p_2$ 这两种情况。当 $p$ 在三角形内部时，上式也成立，正如我们在第 1.3.4 节中所论证的那样。因此，我们得出了以下引理：

引理 1.3.2. 如果 $T = \Delta abc$ 是一个三角形，其顶点式按照逆时针顺序排列的，那么对于平面上任意一点 $p$，下式都成立: $$ \begin{equation}\label{f1.11} \mathcal{A}(T) = \mathcal{A}(p,a,b) + \mathcal{A}(p,b,c) + \mathcal{A}(p, c, a) \end{equation} $$

现在我们可以将这个引理推广到多边形上，写出任意多边形的面积公式。

定理 1.3.3. (多边形的面积). 对于一个多边形 $P$，无论是凸的还是非凸的，以逆时针的顺序排列顶点 $v_0, v_1, \cdots, v_{n-1}$，那么给定平面上任意一点 $p$，都有 $$ \begin{equation}\label{f1.12} \mathcal{A}(P) = \mathcal{A}(p,v_0,v_1) + \mathcal{A}(p, v_1, v_2) + \cdots + \mathcal{A}(p, v_{n-1}, v_{0}) \end{equation} $$ 如果 $v_i = (x_i, y_i)$，那么上式等价于: $$ \begin{align}\label{f1.13} 2 \mathcal{A}(P) & = \sum_{i=0}^{n-1}\left(x_i y_{i+1} - y_i x_{i+1}\right) \\ & = \sum_{i=0}^{n-1}\left(x_i + x_{i+1} \right)\left(y_{i+1} - y_i\right) \end{align} $$

证明： 我们通过数学归纳法证明这个定理。对于 $n = 3$ 的情况，已经有引理 1.3.2 证明成立了。

假设对于所有有 $n -1$ 个顶点的多边形，式($\ref{f1.12}$)都成立。那么对于有 $n$ 个顶点的多边形 $P$ 而言，根据定理 1.2.7，$P$ 有一个耳朵。对 $P$ 的顶点重新编码，使得 $E = (v_{n-2}， v_{n-1}, v_0)$ 对应一个耳朵。移除 $E$ 就得到了多边形 $P_{n-1}$。应用假设，有 $$ \mathcal{A}(P_{n-1}) = \mathcal{A}(p, v_0, v_1) + \cdots + \mathcal{A}(p, v_{n-3}, v_{n-2}) + \mathcal{A}(p, v_{n-2}, v_0) $$ 根据引理 1.3.2，有 $$ \mathcal{A}(E) = \mathcal{A}(p, v_{n-2}, v_{n-1}) + \mathcal{A}(p, v_{n-1}, v_{0}) + \mathcal{A}(p, v_{0}, v_{n-2}) $$ 因为 $\mathcal{A}(P) = \mathcal{A}(P_{n-1}) + \mathcal{A}(E)$，所以 $$ \mathcal{A}(P) = \mathcal{A}(p, v_0, v_1) + \cdots + \mathcal{A}(p, v_{n-3}, v_{n-2}) + \mathcal{A}(p, v_{n-2}, v_0) + \mathcal{A}(p, v_{n-2}, v_{n-1}) + \mathcal{A}(p, v_{n-1}, v_{0}) + \mathcal{A}(p, v_{0}, v_{n-2}) $$ 注意到，$\mathcal{A}(p, v_0, v_{n-2}) = -\mathcal{A}(p, v_{n-2}, v_0)$。这两项抵消之后得到的就是式($\ref{f1.12}$)。□

式(11)中的每一项都可以用一次乘法和两次加法得出，而式($\ref{f1.13}$)则需要两次乘法和一次加法。所以在大多数情况下，第二种形式效率都是更高的。

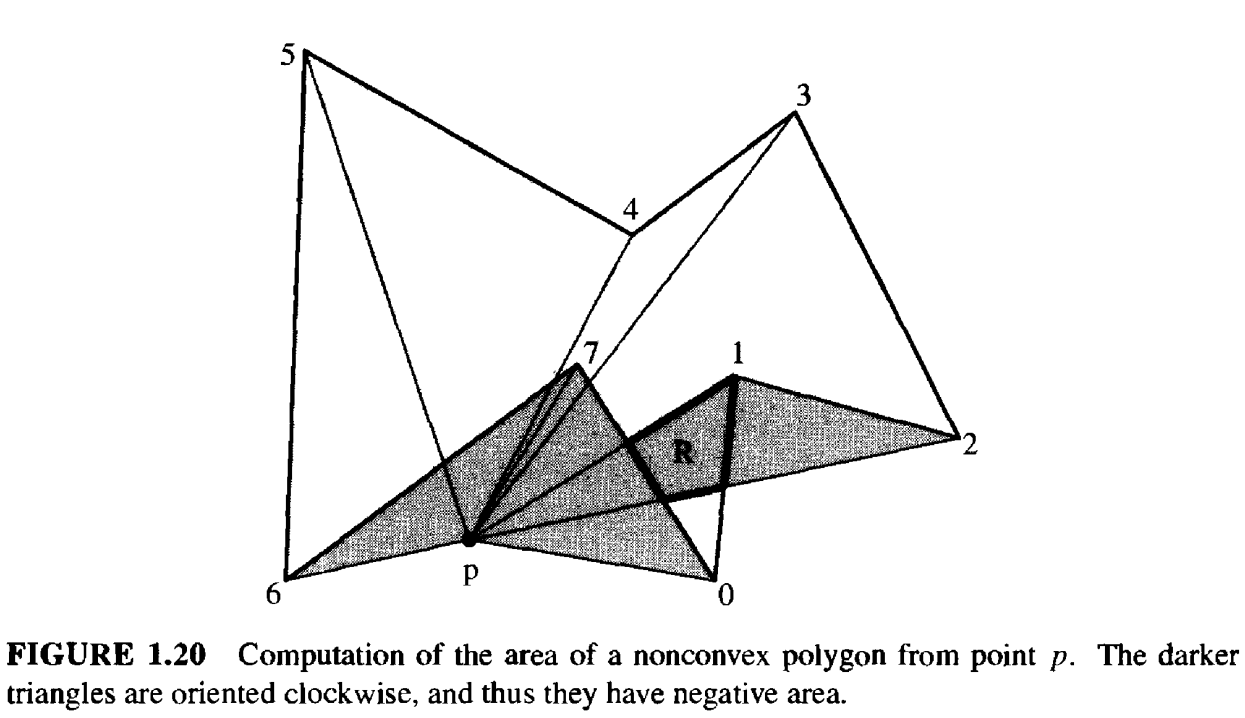
在图 1.20 中，三角形 $\Delta p12, \Delta p67$ 和 $\Delta p70$ 的顶点沿顺时针方向排列，其余三角形都是逆时针排列顶点的。这可以理解为，逆时针方向的三角形的每个顶点上，都附着一个 $+1$ 电荷，而顺时针方向的三角形则附着一个 $-1$ 电荷。因此，位于多边形内部的点 $R$ 被顺时针方向的三角形 $\Delta p12$赋予了一个 -1 电荷。但 $R$ 同时也是另外两个逆时针方向的三角形 $\Delta p01$ 和 $\Delta p23$ 的顶点。所以 $R$ 的净电荷为 $+1$。类似地，多边形 $P$ 内部的每个点的净电荷都是 $+1$，而多边形 P 外部的每个点的净电荷为 0。

1.3.8 三维及更高维度的体积(Volume in Three and Higher Dimension)

引理 1.3.1中通过行列式的形式计算三角形面积有一个优势，它可以直接推广到更高维的空间中。在三维空间中，有一个四面体 $T$，它有四个顶点 $a,b,c,d$，它的体积可以通过下式计算:

$$ \begin{equation}\label{f1.15} 6\mathcal{V}(T) = \begin{bmatrix} a_0 & a_1 & a_2 & 1 \\ b_0 & b_1 & b_2 & 1 \\ c_0 & c_1 & c_2 & 1 \\ d_0 & d_1 & d_2 & 1 \\ \end{bmatrix} = \begin{array}{c} - & (a_2 - d_2)(b_1 - d_1)(c_0 - d_0) & + & (a_1 - d_1)(b_2 - d_2)(c_0 - d_0) \\ + & (a_2 - d_2)(b_0 - d_0)(c_1 - d_1) & - & (a_0 - d_0)(b_2 - d_2)(c_1 - d_1) \\ - & (a_1 - d_1)(b_0 - d_0)(c_2 - d_2) & + & (a_0 - d_0)(b_1 - d_1)(c_2 - d_2) \end{array} \end{equation} $$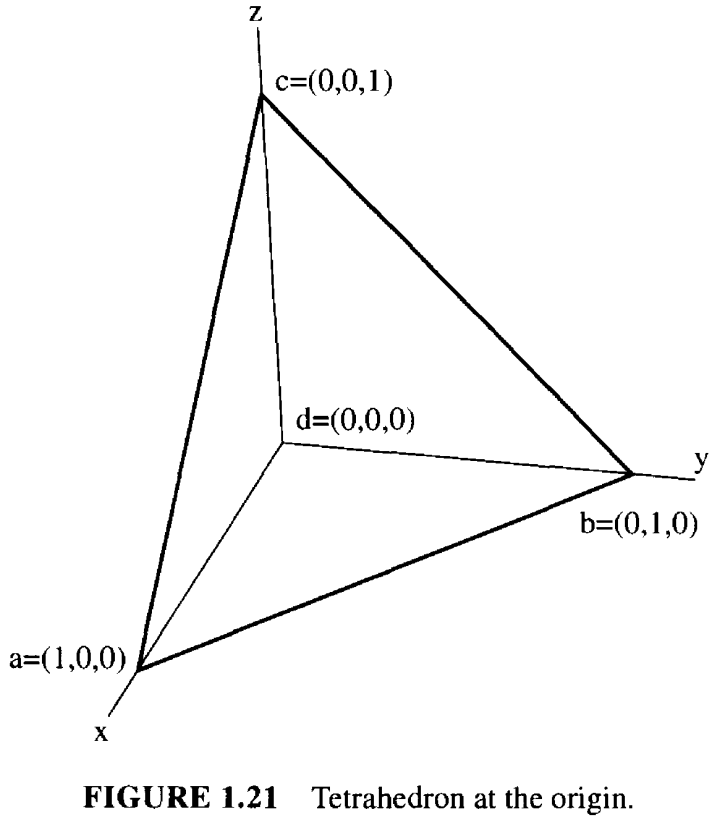

该体积是有符号的。如果顶点 $(a, b, c)$ 成逆时针方向排列时，根据右手定则，$(a,b,c)$确定的平面的法线指向四面体外侧，即远离点 $d$，则该体积为正。如图 1.21 所示，设 $a = (1,0,0), b = (0, 1,0), c = (0,0, 1),d = (0,0,0)$。从外侧看 $(a, b, c)$ 是逆时针方向的。套用公式 ($\ref{f1.15}$) 可得行列式为 1，因此 $\mathcal{V}(T) = 1/6$。这符合底面积乘以高度的规则: $\frac{1}{3} \cdot \frac{1}{2} \cdot 1$。第 4 章将利用这个体积公式来计算三维空间中点的"凸包convex hull"。

值得注意的是，定理 1.3.3 也可以直接扩展。我们可以通过将任意点与多面体的每个三角形面形成的四面体的体积相加来计算多面体的体积（练习 4.7[7]）。这需要，多面体的所有面的法向量都指向外面。

公式 ($\ref{f1.15}$) 也可以推广到更高的 $d$ 维空间中，计算 d-维几何体simplex的体积的 $d!$ 倍。simplex是四面体在更高维空间的扩展。

1.3.9 练习

三重矢量积Triple product。用三重矢量积来解释公式($\ref{f1.4}$)描述的三角形面积行列式。如果 $A,B,C$ 是三维矢量，那么它们的三重矢量积为 $A \cdot (B \times C)$。这是一个标量，其值等于由这三个向量确定的平行六面体的体积。该值与行列式的值相同。 $$ A \cdot (B \times C) = \begin{bmatrix} A_0 & A_1 & A_2 \\ B_0 & B_1 & B_2 \\ C_0 & C_1 & C_2 \\ \end{bmatrix} $$ 假设该行列式是平行六面体的体积，那么方程($\ref{f1.4}$)是所示三角形面积的两倍吗。
[easy] 多边形的方向Orientation of a polygon: from area。给定一个简单多边形的顶点列表，它们按边界遍历顺序排列，如何使用定理 1.3.3 确定其方向(顺时针或逆时针)？
多边形的方向Orientation of a polygon。利用引理 1.2.1 的证明，设计一个更高效的算法来确定多边形的方向。
立方体的体积Volume of a cube。根据公式 $(\ref{f1.12})$，计算边长为 1 的单位立方体的体积，using one vertex as $p$。

1.3 多边形的面积(Area of Polygon)