开发动机与总体框架
1. 开发动机
像人类一样,机器人主要通过身体接触于周围的环境互动。近些年,物理建模在机器人、机器学习、动画、虚拟现实、生物力学等各个领域扮演者越来越重要的角色, 需要精确高效的接触动力学仿真模型(simulation models of contact dynamics)。在机器人开发过程中,仿真一方面用于在真机调试之前,进行控制策略的选择和验证, 以及系统参数的粗调。另一方面应用是,通过大量的数值仿真,对系统运行参数进行辨识,自动化地进行增强学习的训练。针对第二类应用, 接触动力学模型的目标函数还应该有一些适合数值优化的,可导可微之类的数学特性。Mujoco 的底层接触模型就在这方面有着独到的优势。
1.1 软接触
我们放弃了 LCP 算法的核心——严格的互补约束,换得了接触模型的许多优点。我们称这一系列的模型为凸模型(convex)。 对于无摩擦接触,放弃显式的互补约束并不会有什么收益,因为所得到的凸二次规划(convex quadratic program) 的 KKT 最优条件 (Karush-Kuhn-Tucker optimality conditions) 等同于一个 LCP。 但是对于摩擦接触建模的收益巨大。
我们并不将凸模型看做是 LCP 的一种近似,而是将 LCP 模型和凸模型看做是物理现实的不同近似,它们各有其优点和缺点。 通过一个代价函数来替代严格的互补约束,可能会破坏一些互补特性,接触法线方向上的力和速度可以同时为正,并且摩擦力可能不会最大耗散(maximally dissipative)。 一个相关的现象是,引发滑动的唯一方法是在法线方向上产生一些运动。 这些影响虽然在数值上很小,但并不是一个好事。 然而,这个缺点几乎没有实际意义,因为它是以硬接触的假设为前提的。现实中所有物理材料都存在一定程度的变形。这在机器人技术中尤其重要,因为机器人与环境接触的部分通常被设计为柔软的。 对于软接触,必须打破互补性,当存在 penetration and the meterial is pushing the contacting bodies 时,法向的力和速度都是正值。 此外,如果我们从侧面推动一个放置在具有一定 penetration 的柔软表面上的物体时,我们会预计它在开始滑动时,会向上移动一点。 因此,在存在软接触的情况下,我们实际上增加了物理真实感。
当然并不是所有的模型都应该用软接触建模,比如,弹簧阻尼模型就很软,但是它不稳定。因为同一时间不同的材质有不同的特性,所以软模型必须经过充分的参数化,才能应用于多个系统。 这反而有助于接触模型参数的辨识。
1.2 计算效率
具有摩擦解除的保守 LCP 模型是一个 NP 难问题。于是发展出了一个近似求解器的行业,不行的是,很多流行的物理引擎使用的缩写很少有文档说明(poorly-documented shortcuts), 推导出来的运动方程难以表征。实际上,NP 难说的是最坏情况,并不意味着快速地求解 LCP 问题是不可能的。凸优化在求解这类问题时很有优势。在 MuJoCo 中,我们发现 projected Gauss-Seidel(PGS) 只需要 10 此扫描就可以得到一个十分接近全局最小值的解。当然有些问题即使是凸的,也很难通过数值方法求解。对于这类问题,我们还有高阶收敛的共轭梯度求解器。
用途不同,对于计算效率的要求也不一样。如果我们只是需要实时模拟,不追求精度,那么即是求解器恶效率很低,以现代计算机的性能,足以处理大多数的机器人仿真问题。 但是对于优化求解而言,不存在足够快的说法。如果我们能够更快地计算目标函数及其导数,就可以扩大搜索范围、训练集或者是样本大小,从而提高精度和性能。这是我们投入大量精力来开发高效求解器的原因。
1.3 连续时间
库伦摩擦模型在连续的时间上并没有明确的定义,这存在一个 Painleve 悖论。 王俊在他的硕士论文中提到对 Painleve 悖论进行了详细的介绍,在一些特定的情况下,会出现动态自锁的现象,即接触区各点会产生沿着渗透入表面的法向相对加速度。因此离散时间近似和相关的速度步进(velocity-stepping)方案非常流行, 人们很少研究这些模型的连续时间极限。
尽管不是必须的,以前摩擦接触的凸模型也依赖离散时间的近似。Mujoco 所用的模型考虑了力和加速度,是定义在连续时间上的模型,这更接近物理现实。连续时间公式能够进行复杂的数值积分, 不需要离散时间变分积分器的计算。Continuous-time dynamics are also well-defined backward in time, 这个特性在一些优化算法中是需要的。
1.4 逆动力学和优化
逆动力学的目标是在给定多关节系统的位置、速度、加速度的情况下,恢复作用力和接触力。对于硬接触(hard contact)这种计算是不可能的。假设我们推一堵墙,没有发生任何移动, 此是根据运动关系,我们是无法计算接触力的。除非考虑材料的形变,此时我们就需要软接触模型了(soft contact model)。对于这种情况, 通过弹簧—阻尼模型可以轻松计算出接触力,因为它只是一个关于位置和速度的方程,不考虑作用力。忽略作用力将在不可避免的引入误差,引擎就需要不断进行误差校正,导致计算不稳定。 这也是弹簧阻尼模型不受引擎欢迎的一个原因。现代的接触求解器在计算接触力和冲量的时候,都会考虑作用力(以及所有的系统内力),这使得逆动力学的计算变得很难。 实际上 MuJoCo 的逆动力学应该比前向动力学更容易计算,因为可以对优化问题对角化,并将之拆分成若干个独立的子优化问题,which can be solved analytically。
逆动力学在系统辨识、参数估计、运动控制方面的优化算法中扮演着关键的角色。我们可以先以位置序列为优化目标,再通过位置的微分计算速度和加速度,逆动力学则用于计算作用力和接触力, 最后构建关于所有这些变量的优化目标函数。这种方法有多种名称:时空优化(space-time optimization), 谱方法(spectral method), 直接配点法(direct collocation). 在存在接触和其他约束的情况下,MuJoCo 特别适合此类的计算。
2. 总体框架
| symbol | size | description | MuJoCo field |
|---|---|---|---|
| \(n_Q\) | 位置坐标的数量 number of position coordinates | mjModel.nq |
|
| \(n_V\) | 自由度数量 number of degrees of freedom | mjModel.nv |
|
| \(n_C\) | 有效的约束数量 number of active constraint | mjData.nefc |
|
| \(q\) | \(n_Q\) | 关节位置 joint position | mjData.qpos |
| \(v\) | \(n_V\) | 关节速度 joint velocity | mjData.qvel |
| \(\tau\) | \(n_V\) | 作用力 applied force: passive, actuation, external | |
| \(c(q,v)\) | \(n_V\) | bias force: Coriolis, centrifugal, gravitational | mjData.qfrc_bias |
| \(M(q)\) | \(n_V \times n_V\) | 关节空间下的惯量, inertia in joint space | mjData.qM |
| \(J(q)\) | \(n_C \times n_V\) | constraint Jacobian | mjData.efc_J |
| \(r(q)\) | \(n_C\) | constraint residual | mjData.efc_pos |
| \(f(q,v,\tau)\) | \(n_C\) | constraint force | mjData.efc_force |
右表中列举了算法所需要的通用符号,针对特定约束的附加的符号将在后续内容中介绍。
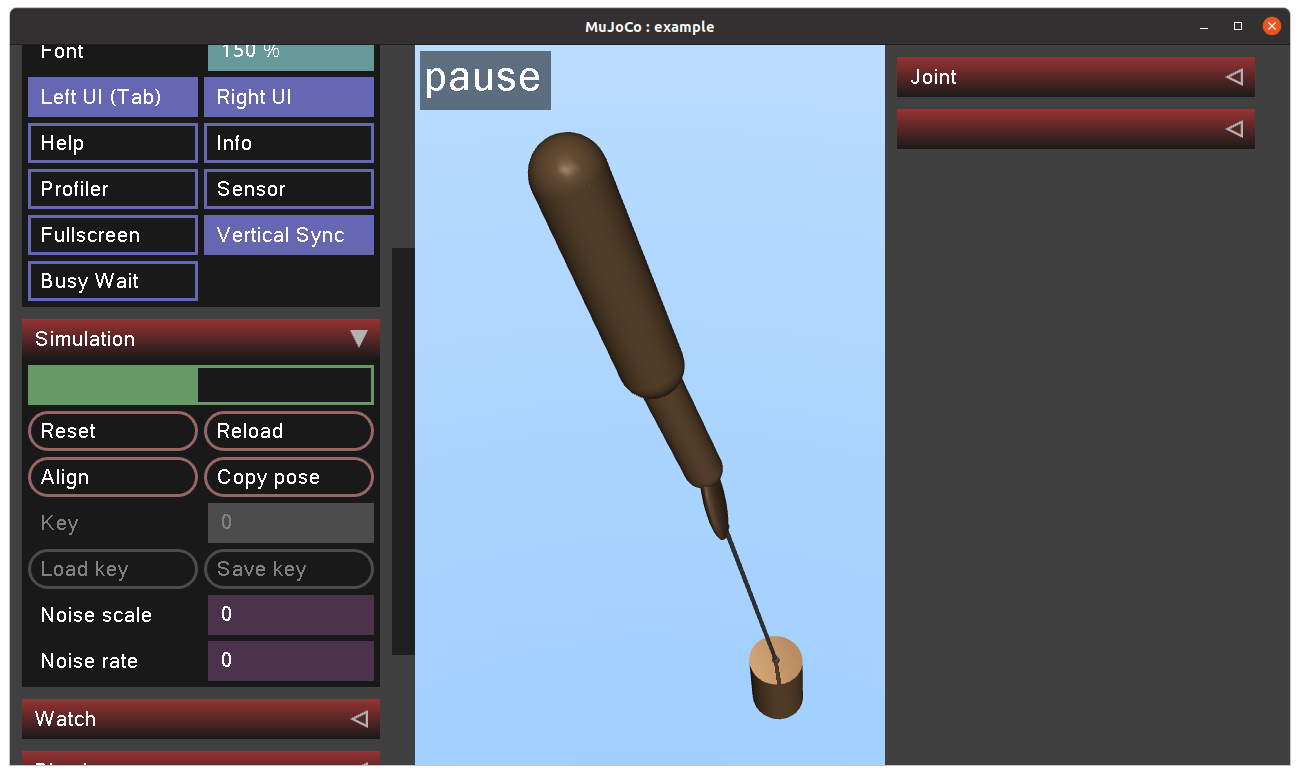
在 MuJoCo 中,所有的模型都在编译的时候构建完毕了(enumerated),并以上面右侧的这些系统级(system-level)的向量和矩阵的形式描述。 上面左侧是模型文件 example.xml 的仿真截图。从上往下分别是, 一个球关节带着一个 'capsule' 形的连杆,通过两个分别绕 y 轴和 x 轴转动的铰链关节连接者一个 'capsule' 形的连杆,再通过两个分别绕 y 轴和 z 轴转动的铰链关节连接者一个 'ellipsoid' 形的连杆。 在连杆的末端通过一个肌腱(tendon)连接着一个自由运动的椭球。整个系统一共有 13 个自由度,球关节有三个、四个铰链个一个、自由运动的椭球有6个自由度,所以其 \(n_V = 13\)。
因为实际的约束在运行的过程中总是在变化的,所以系统的向量和矩阵的 \(n_C\)的维度会有所不同。尽管如此,任然有一个固定的 enumeration order
(取决于出现在 mjModel 的模型的 order)。不知道这个 order 指的是阶数,还是顺序。
那些不活动(inactive)的约束将被忽略掉。
因为我们采用四元数来表示三维位姿,所以当模型中有球关节或者自由关节时,关节坐标的数量\(n_Q\) 要比自由度 \(n_V\)大。在一般意义下,\(\dot{q}\)并不等于\(v\)。
这个 \(\dot{q}\) 应该是指关节坐标的一阶导数?还是四元素的?
通常我们会把描述刚体姿态的旋转矩阵描述成正交群\(SO(3)\),
这个群可以想象成一个四维空间的单位椭球(unit sphere),而刚体的速度则是这个椭球的三维切平面。为了方便计算,
MuJoCo 提供了一个函数 mj_differentiatePos 用于对两个维度为 \(n_Q\) 的位置向量进行差分得到维度为 \(n_V\) 的速度向量。
此外,MuJoCo 还提供了一些有用的四元素计算工具。
MuJoCo 在连续时间上进行前向和逆动力学的解算。我们可以通过 mjModel.opt.timestep 来设定前向动力学的数值积分的时间步长。
连续时间下的一般运动方程可以写作:
雅可比矩阵建立了关节坐标和约束坐标之间的变换关系,它将关节的运动向量(速度和加速度)映射到了约束坐标系下,即关节速度\(v\) 映射到约束坐标系的 \(Jv\)。 雅可比的转置则将约束坐标下的力矢量映射到了关节坐标系下,即约束力\(f\)映射到关节坐标系的\(J^Tf\)。
关节空间下的惯性矩阵 \(M\) 总是可逆的。因此一旦确定了约束力 \(f\),我们就可以写出前向动力学和逆动力学的公式:
$$ \begin{equation}\label{forward_inverse_dynamic} \begin{array}{rl} \text{forward}: & \dot{v} = M^{-1}(\tau + J^Tf - c) \\ \text{inverse}: & \tau = M \dot{v} + c - J^Tf \end{array} \end{equation} $$而约束力的计算是其中的难点,我们将在后续的内容中介绍。上式中其它符号的含义和计算思路如下:
- 作用力 \(\tau\) 包含来自弹簧阻尼器以及流体动力的被动力(passive force)、激励力(actuation forces) 以及用户指定的附加力(additional forces)。
- bias force \(c\) 包含科氏力(Coriolis)、离心力(centrifugal) 和重力(gravitational force)。我们通过加速度为零的递归牛顿欧拉算法(Recursive Newton-Euler, RNE)计算它们的和。
- 关节空间的质量矩阵 \(M\) 则通过复合刚体(Composite Rigid-Body, CRB)算法求得。该矩阵通常都是稀疏的,MuJoCo 以运动树(kinematic tree)的形式表示它。
- 由于我们经常需要将 \(M\) 的逆乘到向量上,所以我们将其分解成\(L^TDL\)的形式,方便以稀疏矩阵的形式存储。当需要计算\(M^{-1}x\)的时候, 就通过稀疏反向带入法(sparse back-substitution)来计算。
在进行上述的计算执勤啊,我们会先通过前向运动学,计算所有空间物体以及关节坐标系的全局位置和姿态。虽然 RNE 和 CRB 算法更适合用在局部坐标系下,但是为了在全局坐标系下进行碰撞检测, 我们还是在全局坐标系下实现的 RNE 和 CRB 算法。此外,为了提高浮点运算的精度,我们将每个运动子树的数据都归结到了其质心的全局坐标系上(对应 mjData 中以 c 开头的字段)。
2.1 激励模型 Actuation model
在 MuJoCo 中,所有的执行器都是单输入单输出的(Single-Input-Single-Output, SISO)。对于一个执行器\(i\),其输入时由用户定义的控制量\(u_i\),这是一个标量,
由 mjData.ctrl 保存。输出也是一个标量\(p_i\),描述的是力矩矢量转换到关节空间的作用力,保存在 mjData.actuator_force。
每个执行器还有一个激励状态的变量\(w_i\),用 mjData.act保存。
通过描述转换关系(Transmission)、激励动力学(activation dynamics) 和力的生成法则(force generation),我们可以定义一个执行器的工作方式。 为了提供最大的灵活性,用户可以按需独立地设置这几个变量,也可以通过快捷配置获得常见的执行器。
- 转换关系,Transmission:描述的是从标量的激励力到关节空间的作用力的映射关系。根据转换关系的类型和参数不同,每个执行器都有一个标量长度 \(l_i(q)\)。 梯度\(\nabla{l_i}\)是一个\(n_V\)维的向量,描述力矩。转换关系的类型有:关节(joint)、 肌腱(tendon)、jointinparent、曲柄滑块(slider-crank)、site、body。
- 激励动力学,Activation Dynamics:诸如气缸、液压缸、生物肌肉这样的执行器,都有一种被称为"activation"的内部状态 internal state。
这确实是关节位置 \(q\) 和速度 \(v\) 之外的一种动力学状态。如果一个模型包含了这样的执行器,那么它的动力学模型将是三阶的。我们用符号\(w\)表示"activation",
根据执行器的 activation type 和相应的模型参数,其一阶导可以表示为 \(\dot{w}_i\left(u_i, w_i, l_i, \dot{i}_i\right)\)。注意每个执行器的动力学特性的定义都与其他执行器无关。
目前实现的 activation type 为:
$$
\begin{array}{rl}
\text{integrator}: & \dot{w}_i = u_i \\
\text{filter}: & \dot{w}_i = (u_i - w_i) / t
\end{array}
$$
其中 \(t\) 是保存在变量
mjModel.actuator_dynprm中的一个时间常量,用户可以通过回调函数 mjcb_act_dyn, 自定义 \(w_i\) 的计算方式。 - 力的生成法则,Force Generation:每个执行器都会生成一个力\(p_i\left(u_i, w_i, l_i, \dot{l}_i\right)\)。各个执行器的力生成机制都是独立的,不能与模型中其他执行器相互作用。
目前,当执行器有激励状态时力就是 affine,and in the control otherwise:
$$
p_i = \left(a w_i \text{ or } a u_i\right) + b_0 + b_1 l_i + b_2 \dot{l}_i
$$
其中 \(a\) 是一个增益系数,\(b_0, b_1, b_2\) 是漂移参数,分别保存在变量
mjModel.actuator_gainprm和mjModel.actuator_biasprm中。我们也可以通过毁掉函数 mjcb_act_gain 和 mjcb_act_bias 自定义增益和漂移的计算方式。 仿射力的生成(affine force generation),使得我们可以利用 moment arms 的伪逆,从作用力(applied force)的逆动力学,推断出控制量/激活量。 但是现实世界中有一些执行器并不是 affine 的,因此我们做了一些扩展。所有的执行器在广义坐标下净力?(net force)为: $$ \sum_i \nabla{l_i}(q) p_i \left(u_i, w_i, l_i(q), \dot{l}_i(q, v)\right) $$ 该值存储在mjDat.qfrc_actuator中,将和用户定义的关节空间或者笛卡尔空间下的力, 分别保存在变量mjData.qfrc_applied和mjData.xfrc_applied中,一起添加到作用力向量\(\tau\)里。
2.2 被动力 Passive forces
被动力是那些只与位置和速度相关的力,它们不能被前向动力学的控制量或者逆动力学的加速度所影响,是前向和逆动力学解算的输入,
保存在 mjData.qfrc_passive 中。在 MuJoCo 的设计里面,被动力是不会增加能量,
但是用户可以通过回调函数 mjcb_passive 向 mjData.qfrc_passive 中添加可能增加能量的力,
只要该力只取决于位置和速度,就不会对 MuJoCo 造成干扰。
MuJoCo 可以计算三种被动力:关节和肌腱中的弹簧阻尼、重力补偿、流体动力。重力补偿是作用在物体质心并与重力相反的力。
当使用欧拉或者隐式积分器时,关节阻尼将被隐式积分,可以显著提高稳定性。因此,尽管阻尼可以用执行器的属性来建模,但是我们还是将其描述成关节的属性。 我们可以通过 XML 中关节属性 springdamper 自动地创建所需时间常数和阻尼比的惯性—弹簧—阻尼器, Mass-Spring-Damper。 这样编译器在计算刚度和阻尼系数时,会考虑到关节的惯性数据。
MuJoCo 并不打算构建复杂的流体动力学,但是我们还是需要提供足够的工具来模拟飞行、游泳等场景。
我们可以通过将变量 mjModel.opt.viscosity 和 mjModel.opt.density 设置为正数来来启用它。
所有的物体都有描述粘度 \(\beta\) 和密度 \(\rho\) 的参数。出于流体动力学的考虑,每个物体的形状都被抽象为等效的惯性盒子(inertia box),这个设定也被用于可视化。 每个盒子的正面(forward-facing, 相对于线速度而言)都有沿其法线方向的力。如果有角速度,那么盒子的所有面都会受到力矩。我们对表面上的力积分,来计算力矩。 我们暂时用 \(v\) 和 \(w\) 来表示局部坐标系下物体的线速度和角速度,3D 向量 \(s\) 表示盒子的尺寸。当考虑所有面的贡献时,第\(i\)个元素在局部坐标系下的力和力矩可以计算如下: $$ \begin{array}{rl} \text{density force}: & - \frac{1}{2} \rho s_j s_k | v_i | v_i \\ \text{density torque}: & - \frac{1}{64} \rho s_i \left(s_j^4 + s_k^4 \right) | w_i | w_i \end{array} $$
该模型隐含着高雷诺数(Reynolds number),升阻比等于攻角的正切。我们还可以设定一个非零的 mjModel.opt.wind 3D 矢量,用于在流体动力学中模拟空速。
每个物体都会受到一个正比于粘度同事反比于线速度和角速度的力和力矩。粘度的设定于密度无关。We use the formulas for a sphere at low Reynolds numbers, with diameter
\(d\) equal to the average of the equivalent inertia box sizes. 其在局部坐标系下的三维力和力矩为。
$$
\begin{array}{rl}
\text{viscosity force}: & -3 \beta \pi d v \\
\text{viscosity torque}: & - \beta \pi d^3 \omega
\end{array}
$$
目前流体动力学的 phenomenological 模型通常只能处理一种情况(e.g. flat vs. spherical objects),很难构建一个广泛适用的高效模型。 比如说,我们知道,低雷诺数时阻力于速度成线性关系,高雷诺数时则是二次关系。 但是,我们目前就不清楚升力如何发生这种转变。 这就使得人们,用密度来计算所有二次力,用粘度来计算所有线性力。如果用户想要使用更好的流体动力学模型,就需要将密度和粘度的参数都设置成零,以关闭 MuJoCo 内置的模拟机制。 我们可以在回调函数 mjcb_passive 中实现自定义的流体动力学。
2.3 数值积分
MuJoCo 在连续时间上计算前向和逆动力学。前向动力学的输出是关节加速度 \(a = \dot{v}\),如果模型中还有执行器的激活状态定义,还会计算\(\dot{w}\)。 这些变量将被用于推进仿真时从 \(t\) 时刻到 \(t+h\)时刻,更新状态变量\(q,v,w\)。有四种数值积分器干这件事, 3个单步的(explicit, semi-implicit, implicit-in-velocity)和一个四阶的龙格库塔。
MuJoCo 并不支持显式的欧拉方法(explicit Euler method),但是有一定的教学意义,它可以写作: $$ \begin{equation}\label{explicit_euler} \begin{array}{rl} \text{activation:} & w_{t+h} = w_t + h \dot{w}_t \\ \text{velocity:} & v_{t+h} = v_t + h a_t \\ \text{position:} & q_{t+h} = q_t + h v_t \end{array} \end{equation} $$
注意对于四元素而言,位置的推理 \(q_t + h v_t\) 就不仅仅是简单的求和,因为\(q\) 和 \(v\) 的维度是不同的。MuJoCo 之所以不是实现显式欧拉方法, 是因为下面半隐式欧拉法(semi-implicit Euler)更好,而且是物理仿真的标准方法:
$$ \begin{equation}\label{semi_implicit_euler} \begin{array}{rcl} v_{t+h} & = & v_t + h a_t \\ q_{t+h} & = & q_t + h v_{t+h} \end{array} \end{equation} $$对比\((\ref{explicit_euler}), (\ref{semi_implicit_euler})\)式,可以看到在半隐式欧拉法中,使用新的速度量来更新位置。隐式欧拉法implicit Euler的形式如下:
$$ \begin{equation}\label{implicit_euler} \begin{array}{rcl} v_{t+h} & = & v_t + h a_{t+h} \\ q_{t+h} & = & q_t + h v_{t+h} \end{array} \end{equation} $$对比\((\ref{semi_implicit_euler}), (\ref{implicit_euler})\)式,隐式欧拉中速度的更新需要用到下一步的加速度\(a_{t+h} = \dot{v}_{t+h}\), 这在时间因果上是不可能的,但是我们可以对其一阶泰勒展开来估算。当展开的形式只与速度相关,跟位置没关系时,就得到了implicit-in-velocity 欧拉法。 这种方法对于,由依赖速度的力,引起的不稳定系统,仿真十分有效。比如多关节摆、空间中翻滚的物体、有升力和阻力的系统、肌腱和执行器构成的阻尼系统。 把加速度写成速度的函数\(a_t = a(v_t)\),速度的更新过程可以写作:
$$ v_{t+h} = v_t + h a(v_{t+h}) $$这是一个关于未知向量\(v_{t+h}\)的非线性方程,可以在每次迭代时对\(a(v_{t+h}\)在\(v_t\)一阶展开,来进行数值求解。前向动力学的形式为:
$$ a(v) = M^{-1}\left(\tau(v) - c(v) + J^T f(v) \right) $$其微分为:
$$ \begin{align} \frac{\partial a(v)}{\partial v} & = M^{-1} D \\ D & \equiv \frac{\partial}{\partial v} \left(\tau(v) - c(v) + J^Tf(v)\right) \end{align} $$那么速度更新可以通过泰勒展开近似得到:
$$ \begin{align} v_{t+h} & = v_t + h a(v_{t+h}) \\ & \approx v_t + h\left(a(v_t) + \frac{\partial a(v)}{\partial v} \cdot (v_{t+h} - v_t) \right) \\ & = v_t + h a(v_t) + h M^{-1} D \cdot (v_{t+h} - v_t) \end{align} $$对上式左乘 \(M\)整理后有:
$$ \begin{equation}\label{implicit_in_velocity} (M - hD)v_{t+h} = (M - hD) v_t + h M a(v_t) \Longrightarrow v_{t+h} = v_t + h(M-hD)^{-1}M a(v_t) \end{equation} $$MuJoCo 中提供的三个单步积分器都是通过式(\(\ref{implicit_in_velocity}\))计算的,只是矩阵\(D\)的形式不同,通常通过数值的方法求得。下面是对MuJoCo提供的四个积分器的简单介绍:
- Semi-implicit with implicit joint damping (Euler): 该方法中,\(D\)只包含关节阻尼的导数。此时 \(D\) 是一个对角阵,\(M- hD\) 是对称的,可以使用 Cholesky 分解。
- Implicit-in-velocity (implicit):该方法中,\(D\)包含了处约束力\(J^Tf(v)\)之外的所有力。虽然我们也可以计算约束力,但是它们很复杂,没有什么收益。
\(D\)不是对称的,不能使用 Cholesky 分解,但是\(D\)和\(M\)都是稀疏的,可以对 \(M - hD\) 记性逆序LU分解,分解结果将保存在
mjData.qLU。 - Fast implicit-in-velocity (implicitfast):该方法中,包含了 implicit 方法的所有力的导数,但是离心力和科氏力 \(c(v)\)是由 RNE 算法计算的。
- 4th-order Runge-Kutta (RK4):在连续时间公式的优点就是可以采用龙格库塔这样的高阶积分器,目前 MuJoCo 中只实现了 4阶的龙格库塔方法,
用户可以通过接口
mj_forward采用自己的积分器。
