P · 光栅的投影矩阵

在上一节中，我们提到只有进入切片空间(Clip Space)的顶点，才会进入片元着色器完成光栅化(rasterize)。而切片空间是一个 xyz 坐标都只有 [-1, 1] 的一个有限空间，模型的顶点坐标经过 M 矩阵和 V 矩阵两次变换之后，转换到相机坐标系下，很容易就超出了这个有限空间。所以例程中的立方体转动到一定角度时，好像有几个地方缺失了，总是显示不全。

我们的眼睛和相机观察到的事物，都是一种从三维空间到二维图像的透视投影。最直观的特征就是近大远小，同一个物体在图像中的尺寸越大，说明它距离我们越近。此外三维空间中平行的两条线，经过透视投影就会在远处相交于一点，而这个点就在遥远的地平线上。读者可以试着修改这个例程中 lookAt 的相机位置参数，会发现无论相机距离立方体多远，立方体的尺寸好像都不会变。

这两个问题可以都可以通过 P 矩阵来解决。针对超出切片空间的问题，我们只需要对相机空间进行一次缩放，保证期望观测的区域都被映射到切片空间中就可以了，如此构造的 P 矩阵，就是一个正交投影，相机的位置并不会改变物体在图像中的尺寸。如果想要近大远小的视觉效果，就需要构建透视投影的 P 矩阵，这个矩阵与针孔相机的内参有很强的关联。

1. 正交投影

我们将一个模型的顶点经过 M 矩阵和 V 矩阵转换到相机坐标系下之后， xyz 坐标很容易超出区间 [-1, 1]，落到切片空间之外，导致模型显示不全。正交投影就可以轻松解决这个问题，它实际是将视图空间做了一次缩放，将模型等比例的映射到了切片空间中。

由于切片空间是一个 $[-1,1]^3$ 的有限空间，所以我们只能对视图空间中的一个限定区域缩放。如右图所示，☺ 在左侧向右观察一个圆柱的端面。为了能够渲染出该圆柱体，我们用宽高深划定了一个立方体，将这个圆柱框住。

接下来的正交投影就是将观察区域立方体的宽高深都缩放到 2，并且需要将相机延 z 轴平移 1，就可以将它的 8 个顶点坐标都映射成 ±1。于是可以直接写出正交投影的映射矩阵如下。

orthorMatrix(2, 2, 2);

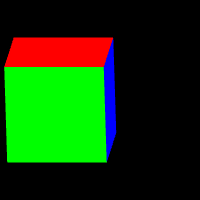
orthorMatrix(2, 2, 1);

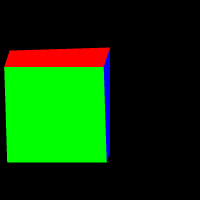
orthorMatrix(2, 2, 0.5);

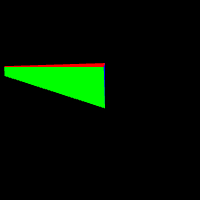
$$ \boldsymbol{P}_{正交投影} = \begin{bmatrix} 2 / width & 0 & 0 & 0 \\ 0 & 2 / height & 0 & 0 \\ 0 & 0 & 2 / depth & 1 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} $$

        // 立方体位姿
        obj.pose.setPosition(0.0, 0, 0, 0);
        obj.pose.setRotation(0.3, 1, 0, 0);
        // 相机位姿
        camera_pose.setPosition(0.5, 0, 1);
        camera_pose.setRotation(0.1, 0, 1, 0);

我们在类 MatrixXf中增加了静态函数 orthorMatrix 用于构建正交投影矩阵。该函数输入 width, height, depth，输出对应的投影矩阵。上面左侧的代码片段是例程中设置的立方体和相机的位姿，如上面右图所示，我们不断加深视图空间的深度值，会看到立方体的逐渐渲染完整。

展开 orthorMatrix>>>

        /**
         * 构造正交投影矩阵
         * @param {number} width 视图空间的宽度 x 轴
         * @param {number} height 视图空间的高度 y 轴
         * @param {number} depth 视图空间的深度 z 轴
         * @param {enum} typeid 矩阵元素的存储类型
         * @returns 4x4 的正交投影矩阵
         */
        static orthorMatrix(width, height, depth, typeid = DataTypeId.FLOAT)
        {
            let m = new Matrix4(typeid);
            m.set(0, 0, 2 / width);
            m.set(1, 1, 2 / height);
            m.set(2, 2, 2 / depth);
            m.set(2, 3, 1);
            return m;
        }

正交投影不存在近大远小的特性，所以立方体转动到不同的角度，渲染出来的形状会有点奇怪，看着不那么像立方体。这可以通过透视投影来解决。正交投影的优势在于，它保留了物体的尺寸比例，所以在机械制图中比较常用。

2. 透视投影

透视投影的近大远小的成像效果，更符合我们对世界的观察经验。如右图所示，透视成像的过程，相当于视图空间的光线都汇聚到相机的过程，每个像素都对应着一束射线，如此就形成了一个四棱锥。在这个四棱锥上，沿着视线方向的每个截面，都被映射到相同大小的 2D 图像上。显然近处的截面要比远处的截面小，于是就有了近大远小的效果。

透视投影也对应者一个矩阵，它负责将这个四棱锥映射到 $[-1,1]^3$ 的切片空间中。我们选定两处截面标记为 near 和 far，得到一个四棱锥台。如下的矩阵可以将该锥台的 8 个顶点坐标都映射成 ±1。

相机位置(-2.0,0,-0.5)

相机位置(-1.0,2,1)

相机位置(-0.7,2,0.5)

$$ \boldsymbol{P}_{透视投影} = \begin{bmatrix} \frac{\cot(0.5 \times fovy)}{aspect} & 0 & 0 & 0 \\ 0 & \cot(0.5 \times fovy) & 0 & 0 \\ 0 & 0 & \frac{far + near}{far - near} & \frac{2 \times near \times far}{far -near} \\ 0 & 0 & -1 & 0 \end{bmatrix} $$

        Matrix4.lookAt(-1.0, 0.0,-0.5, // 相机位置
                       -0.5,-0.0,-0.5, // 目标点
                        0.0, 0.0, 1.0);// 相机参考方向

我们在类 MatrixXf中增加了静态函数 perspectiveMatrix 用于构建透视投影矩阵。上面左侧的代码片段是例程中，通过 lookAt 接口设置的相机的取景方式，如上面右图所示，我们控制相机远离立方体，立方体就会逐渐变小。

展开 perspectiveMatrix>>>

        /**
         * 构造透视投影矩阵
         * @param {number} fovy 垂直视场角, 单位弧度 rad
         * @param {number} aspect 视场的长宽比例(width/height)
         * @param {number} near 近截面到相机的距离
         * @param {number} far 远截面到相机的距离
         * @param {enum} typeid 矩阵元素的存储类型
         * @returns 4x4 正交投影矩阵
         */
        static perspectiveMatrix(fovy, aspect, near, far, typeid = DataTypeId.FLOAT)
        {
            let halffovy = 0.5 * fovy;
            let s = Math.sin(halffovy);
            let ct = Math.cos(halffovy) / s;
            let rdepth = 1.0 / (far - near);
            
            let m = new Matrix4(typeid);
            m.set(0, 0, ct / aspect);
            m.set(1, 1, ct);
            m.set(2, 2, (far + near) * rdepth);
            m.set(2, 3, 2 * near * far * rdepth);
            m.set(3, 2, -1);
            return m;
        }

P · 光栅的投影矩阵

1. 正交投影

2. 透视投影

3. 完