M · 模型的位姿矩阵
对于图形引擎而言,每一个物体都会涉及到一个局部坐标系和一个世界坐标系。我们在局部坐标系下对物体建模,描述物体各个组成部分之间的相对关系。 在世界坐标系下对场景建模,描述各个物体应该以什么姿势摆放在哪里。模型的位姿矩阵(Model Matrix) 建立了两个坐标系之间的联系,通过对物体进行平移、旋转、缩放的变换, 将物体放置到场景中合适的位置上。
点击画布,移动三角形
本质上位姿矩阵(下文中简称 M 矩阵)描述的就是如何移动一个物体,如右侧的例程所示, 点击画布就可以将三角形移动到点击的位置上。本节中,我们将从这个示例出发,介绍 M 矩阵的相关概念和代码实现。
1. 在顶点渲染器中完成物体的移动
渲染物体的通用套路是,在局部坐标系下对物体建模,渲染之前先把建模的顶点坐标通过 VBO 搬运到 GPU 中, 并构造 VAO 将局部坐标系下的顶点映射到顶点渲染器中。 由顶点渲染器负责将 M 矩阵左乘到顶点坐标上,得到世界坐标系下的顶点。下面左侧是例程中使用的顶点渲染器。
左侧第 2 行定义了一个 vec4 类型的变量 pos,用 in 进行修饰表示可以通过 VBO 和 VAO 搬运到 GPU 中并映射进来的一个顶点。 在计算机中,我们常在射影空间下用四维的齐次坐标描述空间中的一个点 \(\boldsymbol{p} = \begin{bmatrix} kx, ky, kz, k \end{bmatrix}\)。\(k\) 是一个比例系数,它取任何非零的值描述的都是同一个点, 所以一般情况下都取 1,即,\(\boldsymbol{p} = \begin{bmatrix} x, y, z, 1 \end{bmatrix}\)。
下面右侧是例程的 js 代码片段,它在一个数组里面顺序定义了三个位于 \(x-y\) 平面上的点。然后通过封装之后的函数 bindArrayBuffer 将顶点坐标的搬运到 GPU 中。 最后用 activateAttribute 将各点的 xyz 坐标映射到顶点渲染器中定义的 "pos" 上。而顶点渲染器中 "pos" 是一个四维的向量,webgl 会将缺少的那一维比例系数置为 1。
#version 300 es
in vec4 pos;
uniform mat4 modelMatrix;
void main() {
gl_Position = modelMatrix * pos;
}
// x, y, z
let positions = [ 0, 0, 0,
1, 0.5, 0,
0, 0.5, 0 ];
let vbo = render.bindArrayBuffer(new Float32Array(positions));
let vao = render.activateAttribute("pos", 3, "float");
顶点渲染器应用 M 矩阵移动物体的关键是上面左侧代码中第 3 行定义的 mat4 类型的矩阵 modelMatrix。
该变量用 uniform 修饰,在渲染物体之前,我们可以用 webgl 的接口 gl.uniformMatrix4fv 修改它,告知顶点渲染器,物体的位置和姿态。
渲染时就在 main 函数中,将该矩阵左乘局部坐标系下的点坐标 pos,得到世界坐标系下的点坐标 gl_Position。
let mat = new XiaoTu.Math.Matrix4();
render.clearColor(1, 0, 0);
render.uniform4fv("uPixelColor", [0, 1, 0, 1]);
render.uniformMatrix4fv("modelMatrix", mat.elements);
render.drawArrays(vao, gl.TRIANGLES);
右侧是进行渲染的 js 代码片段。首先定义了一个 \(4 \times 4\) 的矩阵对象 mat。
类型 Matrix4 是一个矩阵的封装,它实际上就是一个 Float32Array,按列存储矩阵中的元素。
数组中第 i + j * nrows 个元素,对应矩阵中第 \(i\) 行第 \(j\) 列的元素。
矩阵还有一种按行存储的方式,这里之所以要按照列存储,是为了与 OpenGL 的存储方式保持一致。
为了方便,我们在 Matrix4 的构造函数中将它初始化成单位矩阵,表示物体没有任何移动。
接下来的 4 行语句依次完成 ① 将画布背景刷成红色 ② 设置片元着色器中变量 uPixelColor 将要绘制的三角形渲染成绿色 ③ 将单位矩阵搬运到顶点渲染器的 modelMatrix 变量中 ④ 指示 WebGL 上下文进行一次三角形渲染。如此就可以看到例程的初始状态,在一个红色的画布上放置着一个绿色的三角形。下面我们再来看看如何响应鼠标的点击事件,移动三角形。
render.domElement.onmousedown = function(ev) {
let x = 2 * ev.offsetX / render.width() - 1.0;
let y = 1.0 - 2 * ev.offsetY / render.height();
mat.set(0, 3, x);
mat.set(1, 3, y);
render.clearColor(1, 0, 0);
render.uniform4fv("uPixelColor", [0, 1, 0, 1]);
render.uniformMatrix4fv("modelMatrix", mat.elements);
render.drawArrays(vao, gl.TRIANGLES);
}
2. 平移三角形
为了能够响应鼠标的点击事件,我们注册了 onmousedown 事件的回调函数,如右侧的代码所示。每当我们在画布上点击一次鼠标,浏览器都会调用一次该函数,完成一次渲染操作。
该函数有一个输入参数 ev,它详细记录了一次鼠标事件的各种信息。其中 offsetX 和 offsetY 是鼠标点击位置在画布中的像素坐标。我们先在第 2,3 行中做一次坐标映射,得到 webgl 的渲染坐标。
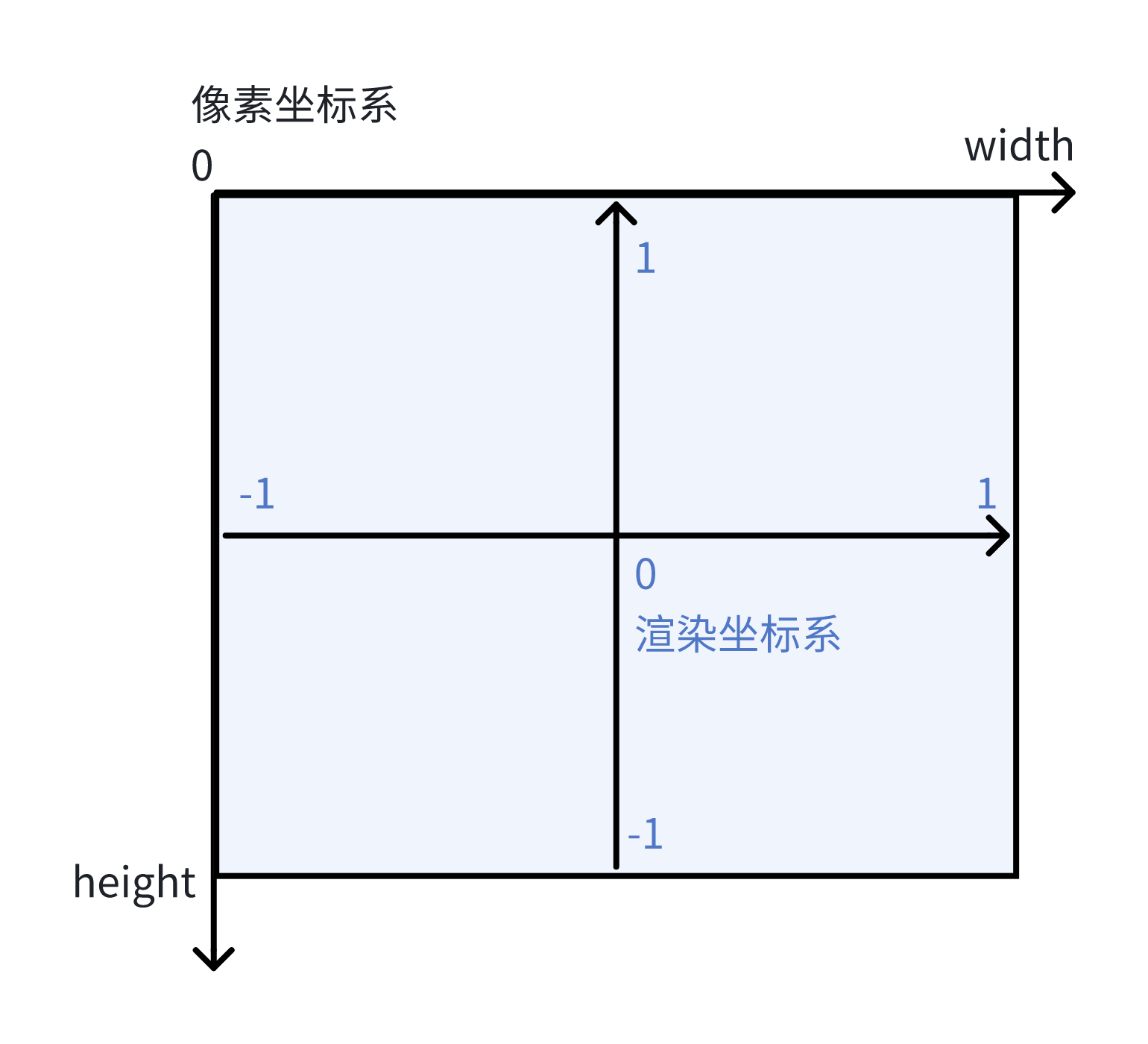
如左图所示,像素坐标系的原点在画布的左上角,x 轴水平向右,y 轴竖直向下。而 WebGL 的渲染坐标系原点在画布的中心,x 轴水平向右,y 轴竖直向上。 像素坐标都是离散的整数,而且其 x 轴的值域是 \([0, \text{width}]\), y 轴的值域是 \([0, \text{height}]\)。 而 WebGL 渲染坐标则是连续的实数,并且 x-y 轴的值域都是 \([-1.0, 1.0]\)。
在接下来的第 4,5 行中,我们将转换后的渲染坐标写到 M 矩阵最后一列的前两行中。M 矩阵是一个 \(4 \times 4\) 的矩阵, 它的详细描述可以参考刚体运动与齐次变换。 可以写成分块的形式 \(M = \begin{bmatrix} \boldsymbol{R}_{3\times 3} & \boldsymbol{t}_{3 \times 1} \\ \boldsymbol{0} & 1 \end{bmatrix}\)。 其中矩阵块 \(\boldsymbol{R}_{3\times 3}\) 是一个 \(3 \times 3\) 的旋转矩阵,描述的是物体在空间中的姿态。 如果是一个单位矩阵 \(\boldsymbol{R}_{3\times 3} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\),则表示物体在空间中没有旋转运动。 三维向量 \(\boldsymbol{t}_{3 \times 1} = \begin{bmatrix} x \\ y \\ z \end{bmatrix}\) 描述的就是物体在空间中的位置。在这里我们只是平移三角形到鼠标点击的位置上, 所以不需要修改旋转矩阵,让它保持单位阵即可,只修改了平移向量中 x,y 的坐标值。在函数的最后,刷新背景色,设置三角形颜色,搬运 M 矩阵到顶点渲染器的 modelMatrix 变量中, 通知 WebGL 上下文完成一帧渲染。就可以看到平移三角形的效果。
class Object3D {
static #instance_count = 0;
#id;
constructor() {
Object3D.prototype.isObject3D = true;
this.#id = Object3D.#instance_count;
Object3D.#instance_count++;
this.pose = new Math.Matrix4();
this.attributes = {};
this.render = null;
this.vao = null;
}
get id() { return this.#id; }
3. 封装 Object3D
现在我们专门封装一个数据类型 Object3D,用来管理物体的 vbo, vao, 位姿矩阵等各个渲染要素。如右侧的代码片段所示。
首先我们希望有一个唯一的 id 来区分各个 Object3D 的实例,这样未来我们构建复杂的渲染场景时可能会方便一些。
所以我们定义了两个私有的成员 #instance_count 和 #id,
其中 #instance_count 还是类的静态成员。
在构造函数中,将 #instance_count 赋值给 #id 之后自增。
这样 #instance_count 可以统计构造的实例数量,并且每个实例的 #id 都是不一样的。
然后用成员变量 pose 来记录物体的位置和姿态,也就是模型的位姿矩阵。字段 attribute 是一个字典,用来记录物体的各种属性,
比如刚才例程中三角形的三个顶点坐标。未来随着 Shader 的功能越来越复杂,可能还会增加顶点的颜色、法向量等属性。
各个属性的键都应当与顶点渲染器(Vetex Shader)中用 in 修饰的变量名保持一致。这样方便我们把具体的数据搬运到 GPU 中构造 VBO 对象。
为了有效管理物体的各种属性,我们还专门封装了一个数据结构 Attribute。
读者有兴趣可以展开下面的代码看看,这里不再详细解释。
class Attribute {
/**
* 构造一个 attribute,渲染时对应一个 vbo
*
* @param {Array|TypedArray} array 数据列表
* @param {int} item_size 每项的元素数量
* @param {string} type 数据类型 float? int?
*/
constructor(array, item_size, type)
{
if (!type in Attribute.creator)
throw TypeError(`Attribute: 不支持的数据类型 ${type}`);
this.type = type;
if (!ArrayBuffer.isView(array))
this.array = Attribute.creator[type](array);
else
this.array = array;
this.item_size = item_size;
this.count = array.length / item_size;
this.length = array.length;
this.vbo = null;
}
static creator = {
float: function(array) {
return new Float32Array(array);
} } }
最后的字段 render 和 vao 用于记录渲染该物体的 WebGL2Renderer 和 VAO 对象。重要的是字段 vao,一旦我们把属性数据搬进 GPU 并构建了 VAO 对象之后,是不需要重复构建的。 我们只需要拿着这个 vao 找 render 进行渲染就行了。
// WebGL2Renderer 新增函数
drawObject3D(obj, pose) {
if (null === obj.render)
obj.render = this;
if (obj.render !== this)
throw ReferenceError("渲染器错误!!!");
我们给 WebGL2Renderer 新增了一个函数 drawObject3D 用于直接渲染一个 Object3D 对象。如左侧的代码片段所示,该函数有两个输入参数。其中 obj 就是渲染对象, pose 则是该对象的 M 矩阵。
虽然我们在 Object3D 中保存了一个姿态矩阵,但这里仍然需要传递一个 M 矩阵的参数。 因为 Object3D 中的姿态矩阵是为后面渲染复杂的多刚体场景准备的,我们需要根据刚体之间的相对位姿关系, 求解出被渲染刚体的 M 矩阵,然后调用该函数完成渲染。
我们需要重点检查一下 obj.vao 这个字段。如果它为空,说明还没有渲染过该物体,它的属性数据也还没搬运到 GPU 中。所以我们先构造一个 VAO 对象。
if (null == obj.vao) {
obj.vao = this.gl.createVertexArray();
this.gl.bindVertexArray(obj.vao);
并在一个 for 循环中为每个属性构建一个 vbo,这里需要保证属性的名称 attr_name 与顶点渲染器中的变量名字对应上。
这样我们就能比较方便的在下面的 13 行中找到对应的变量,完成 VAO 的配置工作。
点击画布,移动三角形
for (const attr_name in obj.attributes) {
let attr = obj.attributes[attr_name];
attr.vbo = this.bindArrayBuffer(attr.array);
let location = this.gl.getAttribLocation(this.program, attr_name);
this.gl.vertexAttribPointer(location, attr.item_size,
_gl_type_map_[attr.type], false, 0, 0);
this.gl.enableVertexAttribArray(location);
} }
在有 VAO 对象的情况下,我们就先更新模型的 M 矩阵,再通过 bindVertexArray 接口切换到 obj.vao 上,最后就可以调用 drawArrays 函数完成渲染。 右侧的例程就是用 drawObject3D 渲染出来的。
this.uniformMatrix4fv("modelMatrix", pose.elements);
this.gl.bindVertexArray(obj.vao);
this.gl.drawArrays(this.gl.TRIANGLES, 0, obj.attributes.pos.count);
}
4. 空间中旋转的立方体
大多数时候,我们渲染的物体都是由若干个三角形拼接出来的。比如我们想要渲染一个彩色的立方体,给每一个面指定一个颜色。 就可以通过如下的代码实现。
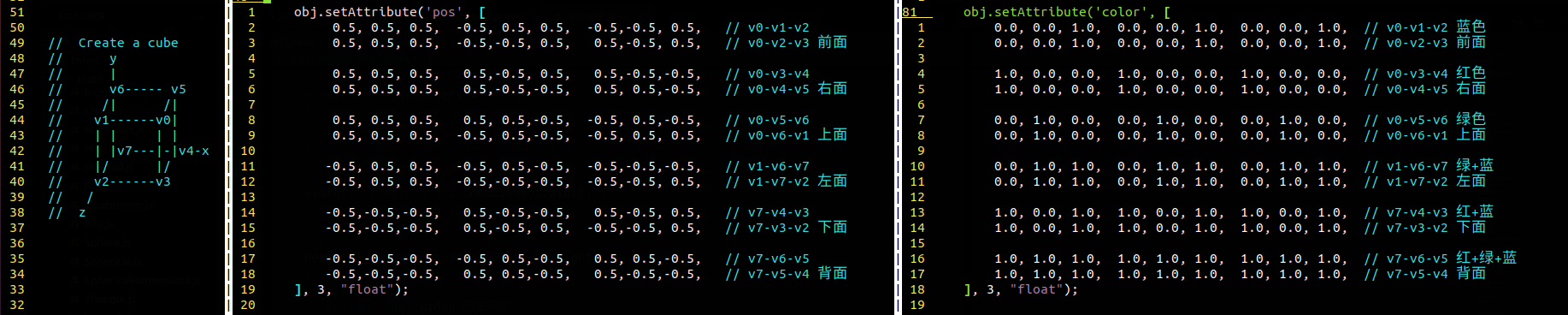
需要注意的是,一个平面实际上是有两个面的,我们应当按照逆时针的方向给出各个顶点的坐标。这样按照右手坐标系,立方体的各个面的法向量都是向外的, OpenGL 才能正确的判定各个面的遮挡关系。此外为了处理遮挡关系,我们还对 WebGL2Renderer 的成员函数 clearColor 做了一点修改,如下代码中第3,6行, 开启了深度检测,并清除深度缓冲区。否则我们就会看到立方体里面,如下面右图所示,这是不合理的。

clearColor(r = 0.0, g = 0.0, b = 0.0, a = 1.0) {
let gl = this.gl;
gl.enable(gl.DEPTH_TEST);
gl.clearColor(r, g, b, a);
gl.clear(gl.COLOR_BUFFER_BIT);
gl.clear(gl.DEPTH_BUFFER_BIT);
}
我们在例程的最后定义了一个函数 doRender(),如下第 8 行所示, 该函数运行结束之后,会通过浏览器的接口 requestAnimationFrame 再次调用一次该函数,从而实现动画的效果。在第 6 行中,我们调用了一个在 Matrix4 中封装的函数, 该函数通过罗德里格斯公式,实现了指定任意旋转轴转动一定角度的旋转矩阵。 通过修改转轴只绕着 x 轴或者 y 轴转动立方体,我们会看到它是顺时针转动的。 查阅了一些资料之后,确认这个绘图窗口(ClipSpace)是一个左手坐标系。 如下面中间的图所示。后面我们会通过相机的视角矩阵来保证图形引擎是右手坐标系的。

let rad = 0;
let rotationSpeed = 0.001;
function doRender() {
render.clearColor(0, 0, 0);
rad += rotationSpeed;
obj.pose.setRotation(rad, 1, 1, 1);
render.drawObject3D(obj, obj.pose);
requestAnimationFrame(doRender);
}
doRender();
