V · 相机的视角矩阵
入门教程提到 WebGL 主要是通过顶点渲染器 vertex shader 和 片元着色器 fragment shader 将三维的模型渲染成 2D 的图像。顶点渲染器用于计算点坐标,片元着色器用于计算颜色。用 OpenGL 的术语来说,顶点渲染器负责将模型的顶点映射到标准坐标下(Normalized Device Coordinates, NDC)。 这个空间也被称为切片空间(Clip Space),其中所有点的 xyz 坐标都在 \([-1, 1]\) 的区间内。超出该区间的点将不会进入片元着色器完成光栅化(rasterize)。所谓的光栅化, 主要是在计算各个面片(一般是三角形)覆盖的像素位置,根据顶点的颜色、法向量等属性对覆盖的像素进行插值。然后经过深度检测、遮挡关系判定,确定各个像素应该渲染哪个面片,最终得到一幅 2D 的渲染图像。
本部分所介绍的 MVP 矩阵,依次通过三个变换矩阵,将模型的各个顶点映射到切片空间中。 上一节中我们介绍了 M 矩阵,最终实现了一个旋转的立方体。但是由于 WebGL 的切片空间是一个左手坐标系, 所以立方体的旋转方向跟我们预期的逆时针有些出入。本节我们介绍 V 矩阵。对于切片空间的左手坐标系的问题,我们直接在顶点渲染器中,将最后映射到切片空间的 z 轴坐标取反,得到一个右手坐标。
1. 渲染图像的坐标系
在 MVP 的框架下,如果把光栅化的过程也看做一次变换的话,一个立方体从建模到渲染出 2D 图片,大体上要经过 4 个变换 5 个空间。 下图需要从右往左看。首先我们需要在一个局部的坐标系下,对物体建模,这个空间被称为局部空间(local space)。 我们把一个 \(4 \times 4\) 的 M 矩阵(Model Matrix)左乘到顶点坐标上,就将立方体摆放到了世界坐标系下, 也就是所谓的全局空间(global space)。
如中间的图所示,世界坐标系下还有一个相机,在原点的正上方向下看。如果我们把相机的位姿写成一个 \(4 \times 4\) 的矩阵,该矩阵的逆就是本文要探讨的 V 矩阵。 再把 V 矩阵(View Matrix) 左乘到世界坐标系下的顶点坐标上,就可以得到相机坐标系下模型的位姿,对应的就是视图空间(Camera Space)。
相机有一个视场角 (FOV,Field Of View) 的概念,他只能对视场角内的一个椎体成像。而且成像的过程是一种透视投影,也就是我们常说的近大远小的效果。 下一节将要介绍的投影矩阵 P 也是一个 \(4 \times 4\) 的矩阵,将它左乘到相机空间的顶点坐标上, 就来到了切片空间。该坐标空间下所有点的 xyz 坐标都在 \([-1, 1]\) 的区间内,超出该区间的点将不会进入片元着色器完成光栅化(rasterize)。 如下图所示,最后将切片空间中的顶点送去光栅化,经过片元着色器(fragment shader)的处理

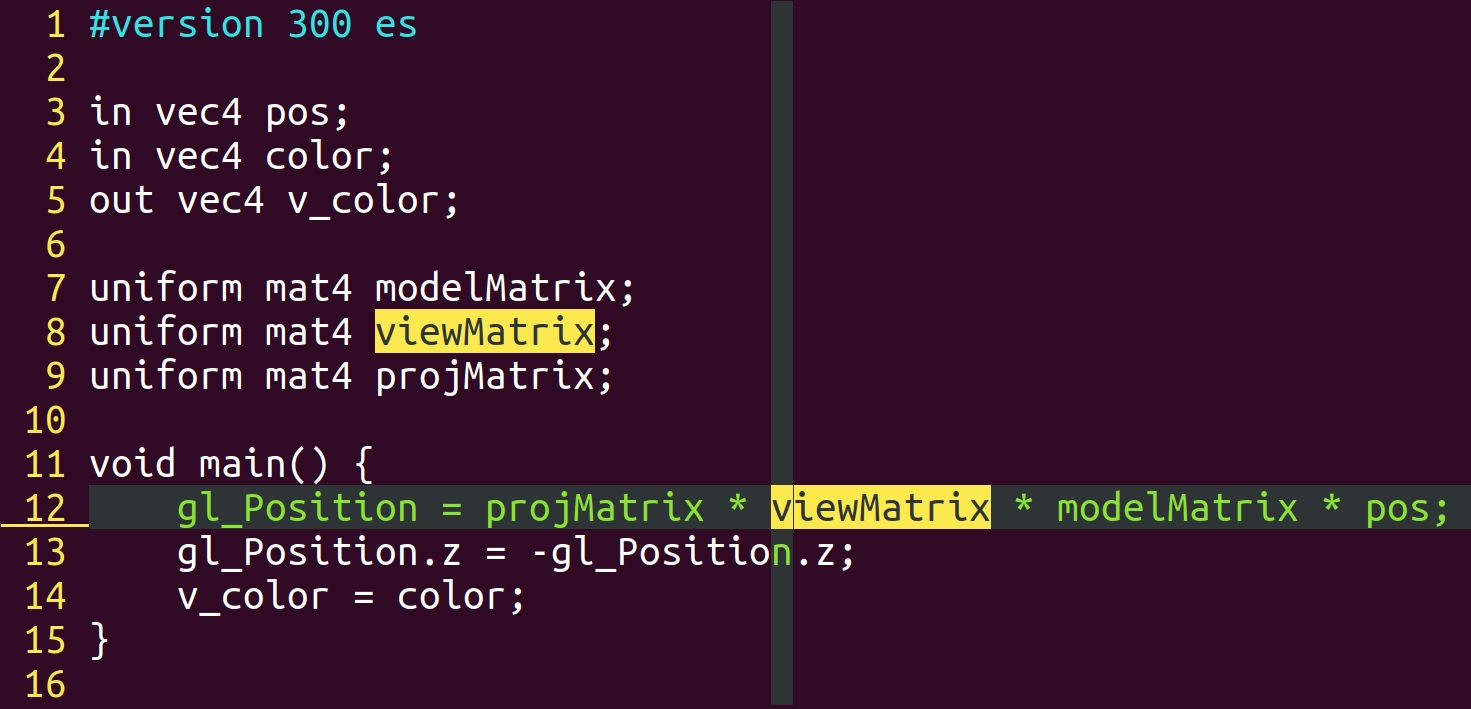
前 3 个变换,分别对应着 MVP 三个矩阵,它们都是在顶点渲染器中完成的。右图给出了本文和下一节 将要使用顶点渲染器程序。在该程序中我们定义了 modelMatrix, viewMatrix 和 projMatrix, 分别对应模型的位姿矩阵、相机的视角矩阵、光栅的投影矩阵。该程序运行结束后,得到的 gl_Position 就是切片空间中的点了。
有一点需要注意的是,最后这个切片空间,它并不是我们熟悉的右手坐标系。 所以上一节最后旋转立方体的颜色和转动方向都有些问题。要处理它也很简单,我们只需要将矩阵 \( \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}\) 左乘到 P 矩阵上就可以了。这相当于左乘到向量 gl_Position 上,也就是对其中的 z 轴数据取反,所以我们在 main 函数中增加了第 13 行,用于得到一个右手坐标系的切片空间。

2. 移动相机位置
如右图所示,我们可以把渲染的过程,想象成一个小人拿着相机飞在空中对场景拍照。小人在空中的位置和姿态,决定了它能够以什么视角观测场景。 根据坐标变换关系,相机的视角矩阵实际上就是小人位姿矩阵的逆。
我们对上一节最后渲染立方体的例程,做了一些修改。我按照个人习惯调整了坐标方向,如下面左一的注释图所示, 令 z 轴朝上。由于我们修改右手坐标系的时候,在顶点渲染器中只对经过投影变换后的 z 轴取反,所以默认情况下 x 轴朝右,y 轴朝后。
中间的图和右一分别是立方体各面的顶点坐标和颜色。这里将顶点坐标写成 -0.5 或者 0.5 是为了让立方体能够落在最后的切片空间中。

let camera_pose = new XiaoTu.Math.Matrix4();
camera_pose.setPosition(0.5, 0, 1);
camera_pose.setRotation(0.1, 0, 1, 0);
//! 需要对相机位姿求逆才能得到视角矩阵
let v_mat = camera_pose.clone().inverse();
render.uniformMatrix4fv("viewMatrix", v_mat.elements);
如右侧的代码片段所示,我们定义了一个 \(4 \times 4\) 的齐次变换矩阵来描述相机的位姿。第 2 行将相机靠右 0.5 摆放在 z = 1.0 的位置上。 我们可以从最右侧的渲染效果中看到,立方体整体向左偏移了。
第 3 行中我们让相机绕着 y 轴逆时针转动了一点,所以渲染图中始终会看到一点点蓝色的立方体右面。camera_pose 描述的是在世界坐标系下相机的位姿。 我们希望得到的是,相机视角下世界的样子,所以需要对相机的位姿矩阵求逆,得到的才是视角矩阵,如第 5 行所示。
我们特意让立方体绕着自身的 x 轴转动,依次会在渲染图中看到,立方体的上面(绿色)、后面(红色)、下面(红蓝)、前面(绿蓝)。注意观察立方体的旋转过程, 会发现立方体转动到一定角度时,好像有几个地方缺失了。这是因为最后得到的顶点坐标超出了切片空间导致的, 下一节介绍的投影矩阵就会解决掉这一问题。
3. LookAt
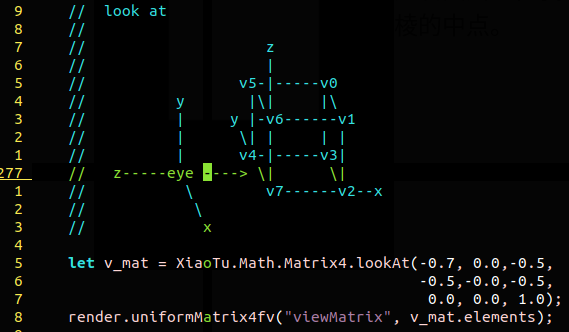
手写相机的位姿矩阵比较麻烦,写错了就可能导致顶点超出切片空间,不出图,定位问题也比较头疼。一种比较常用的重置相机位姿的方法就是 LookAt。如其字面意思那样, 该算法就是要给出相机看向某个点的视角矩阵。为此我们实现了一个 lookAt 的函数。
如右图所示,我们从世界坐标 \((-0.7, 0.0, -0.5)\) 的位置上看向立方体左面下棱的中点 \((-0.5, 0.0, -0.5)\)。最后一组 \((0.0, 0.0, 1.0)\) 是相机 y 轴的参考方向。 渲染效果如左图所示。参考例程。
假设相机在 \(\boldsymbol{c}\) 的位置上,观察的目标点为 \(\boldsymbol{p}\),那么向量 \(\vec{\boldsymbol{pc}} = \boldsymbol{c} - \boldsymbol{p}\) 就是相机位姿的 z 轴方向。 如果不指定 y 轴的参考方向,那么相机可以在垂直于向量 \(\vec{\boldsymbol{pc}} \) 的平面上任意旋转。 我们可以选择任意一个不平行于 \(\vec{\boldsymbol{pc}}\) 的向量 \(\boldsymbol{r}\) 作为 y 轴的参考向量。 \(\boldsymbol{r}\) 的选择不同,就会看到相机转动不同的角度。
将向量 \(\vec{\boldsymbol{pc}}\) 与参考向量 \(\boldsymbol{r}\) 作一次叉乘运算,就可以得到一个垂直于 \(\vec{\boldsymbol{pc}}\) 的向量 \(\boldsymbol{s}\), 该向量可以作为相机位姿的 x 轴方向。由于向量 \(\boldsymbol{r}\) 的选择比较随意,它不一定与 \(\vec{\boldsymbol{pc}}\) 垂直。 我们再将 \(\vec{\boldsymbol{pc}}\) 与 \(\boldsymbol{s}\) 作一次叉乘,就会得到一个同时垂直于 \(\vec{\boldsymbol{pc}}, \boldsymbol{s}\) 的向量 \(\boldsymbol{f}\), 该向量就是相机位姿的 y 轴方向。假设这三个向量的模长都是 1,将这三个向量按列排列 \(\begin{bmatrix} \boldsymbol{s} & \boldsymbol{f} & \vec{\boldsymbol{pc}} \end{bmatrix}\) 得到的就是相机的旋转矩阵 \(\boldsymbol{R}\)。结合向量 \(\vec{\boldsymbol{pc}}\) 就可以得到相机的位姿矩阵 \(\begin{bmatrix} \boldsymbol{R} & \vec{\boldsymbol{pc}} \\ \boldsymbol{0} & 1\end{bmatrix}\)。 由于旋转矩阵是个正交矩阵,所以按行排列的 \(\begin{bmatrix} \boldsymbol{s}^T \\ \boldsymbol{f}^T \\ \vec{\boldsymbol{pc}}^T \end{bmatrix}\) 就是旋转矩阵的逆 \(R^{-1}\)。 根据齐次矩阵的求逆公式 \( \begin{equation}\label{f31} H^{-1} = \begin{bmatrix} R^T & -R^T\vec{\boldsymbol{pc}} \\ \boldsymbol{0} & 1 \end{bmatrix} \end{equation} \) 可以很容易写出相机的视角矩阵。
