加快QR算法的收敛过程

其一，压缩每次迭代的运算量。也就是想办法避免，复杂度较高的 QR 分解和乘法运算。这点可以通过隐式QR迭代算法来实现。
其二，加快迭代的收敛过程。要么对矩阵做些预处理选择一个合理的迭代初值，要么迭代过程中对矩阵做些变形加快收敛。

本文我们从 Schur 分解定理出发，研究一种常用的初值 Hessenberg 矩阵。再研究带偏移量的 QR 迭代法，该方法与带偏移量的逆幂法类似，可以加快收敛。

1. Schur 分解定理

在复数域 $\mathbb{C}$ 中，任何一个$n \times n$ 的方阵 $\boldsymbol{A} \in \mathbb{C}^{n\times n}$，都可以通过酉矩阵 $\boldsymbol{Q}$变换成一个上三角矩阵 $\boldsymbol{U}$。即，$\boldsymbol{Q}^*\boldsymbol{A}\boldsymbol{Q} = \boldsymbol{U}$。其中 $\boldsymbol{Q}^*$ 是矩阵 $\boldsymbol{Q}$ 的共轭转置。酉矩阵是正交矩阵在复数域上的推广，在复数域 $\mathbb{C}$ 中，如果一个矩阵 $\boldsymbol{Q}$ 的共轭转置$\boldsymbol{Q}^*$就是它的逆 $\boldsymbol{U}^{-1}$，那么我们就称 $\boldsymbol{U}$ 为酉矩阵。该矩阵具有性质 $\boldsymbol{U}^* \boldsymbol{U} = \boldsymbol{U} \boldsymbol{U}^* = \boldsymbol{I}$。这就是著名的 Schur 分解定理。它可以通过数学归纳法来证明，网络上有很多资料，这里不再重复了。

在实数域 $\mathbb{R}$ 中，矩阵 $\boldsymbol{A}$ 的特征值有可能是个复数。此时就不能在实数域中，找到一个正交矩阵 $\boldsymbol{Q}$ 将其相似变换到上三角矩阵中了。因为相似变换会保持矩阵的特征值不变，而上三角矩阵的对角线上的元素就是其特征值。如果在域 $\mathbb{R}$ 中 $\boldsymbol{A}$ 与上三角矩阵 $\boldsymbol{U}$ 相似，那么 $\boldsymbol{U}$ 对角线上的元素就是 $\boldsymbol{A}$ 的特征值。这与 $\boldsymbol{A}$ 存在复特征值矛盾。

尽管如此，在实数域 $\mathbb{R}$ 中，我们还是可以将任意的 $\boldsymbol{A}$ 相似变换到一个十分接近上三角形式的矩阵 $\boldsymbol{R}$ 上。有 实 Schur 分解定理:

对于实数域中的方阵 $\boldsymbol{A} \in \mathbb{R}^{n \times n}$，都存在一个正交矩阵 $\boldsymbol{Q} \in \mathbb{R}^{n \times n}$，使得 $\boldsymbol{A}$ 相似于一个近似上三角的矩阵 $\boldsymbol{R}$，即 $$ \boldsymbol{Q}^T\boldsymbol{A}\boldsymbol{Q} = \begin{bmatrix} \boldsymbol{R}_{11} & \boldsymbol{*} & \cdots & \boldsymbol{*} \\ \boldsymbol{0} & \boldsymbol{R}_{22} & \cdots & \boldsymbol{*} \\ \vdots & \vdots & \ddots & \vdots \\ \boldsymbol{0} & \boldsymbol{0} & \cdots & \boldsymbol{R}_{kk} \\ \end{bmatrix} $$ 其中，$\boldsymbol{R}_{ii}$ 是 $1 \times 1$ 或者 $2 \times 2$ 的矩阵块。若 $\boldsymbol{R}_{ii}$ 是一个 $1 \times 1$ 的矩阵块，那么其中唯一的那个元素就是矩阵 $\boldsymbol{A}$ 的特征值。如果是一个 $2 \times 2$ 的矩阵块，那么该矩阵块就对应着 $\boldsymbol{A}$ 的一堆共轭复特征值。

看到这两个定理之后，我一直觉得 QR 迭代最后的收敛形式就是这个 Schur 分解，但是我一直没有找到证明过程，也有可能是没看懂错过了。我看到很多材料都在说，进行 QR 迭代之前可以先将目标矩阵相似到一个 Hessenberg 形式的矩阵上，在后续的迭代过程中迭代矩阵将一直保持 Hessenberg 的形式。但是我在想 Schur 分解得到的近似上三角矩阵也是 Hessenberg 形式呀。QR 迭代要收敛到上三角矩阵，Schur 分解看样子像是最简形式呀，要收敛不应该就刚刚好到这种形式上吗。

2. Hessenberg 矩阵

在一个 $n \times n$ 的矩阵中，如果 $a_{ij} = 0$ 对所有 $i > j + 1$ 的元素都成立，那么它就是上 Hessenberg 形式的矩阵。如果对所有 $j > i + 1$ 的元素都成立，那么它就是下 Hessenberg 形式的矩阵。如下所示，如果下次对角线以下的所有元素为 0 的矩阵就是上Hessenberg矩阵。如果上次对角线以上的元素全为 0 就是下Hessenberg矩阵。显然，对角阵、三角阵都是 Hessenberg 阵。这里我们只关注上 Hessenberg 矩阵。

$$ \underbrace{\begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ 0 & a_{32} & a_{33} & a_{34} \\ 0 & 0 & a_{43} & a_{44} \\ \end{bmatrix}}_{上Hessenberg矩阵} \qquad \underbrace{\begin{bmatrix} a_{11} & a_{12} & 0 & 0 \\ a_{21} & a_{22} & a_{23} & 0 \\ a_{31} & a_{32} & a_{33} & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} \\ \end{bmatrix}}_{下Hessenberg矩阵} $$

任何方阵都可以通过 Householder 矩阵转换成 Hessenberg 矩阵。给定任意向量$\boldsymbol{x} = \begin{bmatrix} x_1 & \cdots & x_n \end{bmatrix}^T$ 我们总是可以构造出一个 Householder 矩阵 $\boldsymbol{H}$，将其映射到向量 $\boldsymbol{y} = \begin{bmatrix} \alpha & \cdots & 0 \end{bmatrix}^T$ 上，其中 $\alpha = \pm \| \boldsymbol{x} \|$。Householder 矩阵 $\boldsymbol{H}$ 本身就是正交的。利用这两个特性，就可以构造相似变换，消除次对角线以下的元素。比如说一个 $4 \times 4$ 的矩阵 $ \boldsymbol{A} = \begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ \hline a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} \\ \end{bmatrix} $ 我们需要对其进行相似变换之后，使得 $a_{31}, a_{41}, a_{42}$ 所在位置的元素为0。对于第一列，我们可以先根据子向量 $\boldsymbol{a}_{21} = \begin{bmatrix} a_{21} \\ a_{31} \\ a_{41} \end{bmatrix}$ 构建一个 $3\times 3$ 的 Householder 矩阵 $\boldsymbol{H}_{21}$，进而构造块对角矩阵 $\boldsymbol{Q}_{1} = \begin{bmatrix} 1 & \boldsymbol{0} \\ \boldsymbol{0} & \boldsymbol{H}_{21}\end{bmatrix}$。因为 $\boldsymbol{Q}_1$ 的左上对角块是个 $1 \times 1$ 的单位矩阵，所以它左乘矩阵 $\boldsymbol{A}$ 将保持第一行不变，同时消除第一列的最后两项。矩阵 $\boldsymbol{Q}_1$ 的转置也是相同形式的块对角矩阵 $\boldsymbol{Q}_{1}^T = \begin{bmatrix} 1 & \boldsymbol{0} \\ \boldsymbol{0} & \boldsymbol{H}_{21}^T\end{bmatrix}$。所以将其右乘到矩阵之后将保持原矩阵的第一列不变，于是有 $ \boldsymbol{A}_2 = \boldsymbol{Q}_1\boldsymbol{A}\boldsymbol{Q}_1^T = \left[ \begin{array}{c|c} a_{11} & \begin{array}{} \tilde{a}_{12} & \tilde{a}_{13} & \tilde{a}_{14} \end{array} \\ \hline \begin{array}{} \tilde{a}_{21} \\ 0 \\ 0 \end{array} & \begin{array}{} \tilde{a}_{22} & \tilde{a}_{23} & \tilde{a}_{24} \\ \hline \tilde{a}_{32} & \tilde{a}_{33} & \tilde{a}_{34} \\ \tilde{a}_{42} & \tilde{a}_{43} & \tilde{a}_{44} \\ \end{array} \end{array} \right] $。然后我们对第二列的子向量 $\tilde{\boldsymbol{a}}_{22} = \begin{bmatrix} \tilde{a}_{32} \\ \tilde{a}_{42} \end{bmatrix}$ 构造 $2 \times 2$ 的矩阵 $\boldsymbol{H}_{32}$，进而构造块对角矩阵 $\boldsymbol{Q}_2 = \begin{bmatrix} 1 & & \\ & 1 & \\ & & \boldsymbol{H}_{32} \end{bmatrix}$。于是有 $ \boldsymbol{A}_3 = \boldsymbol{Q}_1\boldsymbol{A}_2\boldsymbol{Q}_1^T = \begin{bmatrix} a_{11} & \tilde{a}_{12} & \tilde{a}_{13} & \tilde{a}_{14} \\ \tilde{a}_{21} & \tilde{a}_{22} & \tilde{a}_{23} & \tilde{a}_{24} \\ 0 & \tilde{a}_{32} & \tilde{a}_{33} & \tilde{a}_{34} \\ 0 & 0 & \tilde{a}_{43} & \tilde{a}_{44} \\ \end{bmatrix} $。

完整的实现，参见例程 UpperHessenberg。

3. QR 迭代收敛对比

我们可以通过一次迭代前后矩阵的差 $\boldsymbol{A}_{k+1} - \boldsymbol{A}_{k}$ 中最大绝对值是否小于一个很小的数来判定算法是否收敛了。即，$\max(|\boldsymbol{A}_{k+1}(i,j) - \boldsymbol{A}_{k}(i,j)|) < \varepsilon$。为了验证算法的收敛速度，我们在 EigenShiftQR 中用成员函数 NaiveIterate 重新实现了一遍朴素的 QR 迭代。一方面引入了算法收敛的判定，收敛后将终止迭代并返回实际迭代次数。另一方面优化了一些数据结构，避免在迭代过程中频繁构建并销毁对象。细节还请查看代码。

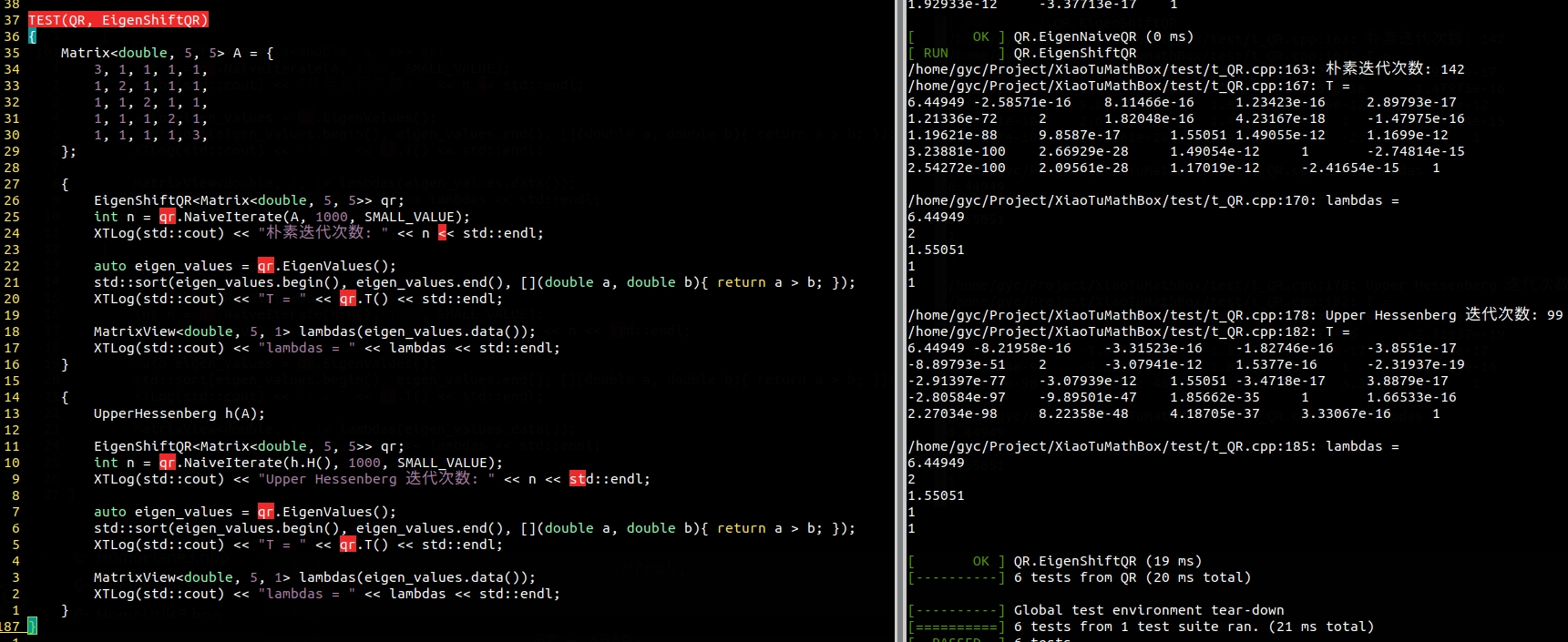
如下截图所示，我们对$5 \times 5$的矩阵 $\begin{bmatrix} 3& 1& 1& 1& 1 \\ 1& 2& 1& 1& 1 \\ 1& 1& 2& 1& 1 \\ 1& 1& 1& 2& 1 \\ 1& 1& 1& 1& 3 \\ \end{bmatrix}$ 分别使用朴素的 QR 和经过 Hessenberg 矩阵预处理的朴素QR迭代。从日志结果来看，朴素QR需要迭代142次，而Hessenberg预处理之后则只需要99次。看起来有个好初值收敛会快一点。

4. 带偏移量的 QR 迭代法

1:	若 $\max(\|\boldsymbol{A}_{k+1}(i,j) - \boldsymbol{A}_{k}(i,j)\|) ≥ \varepsilon$ 则:
2:	选择一个偏移量 $\sigma_k$
3:	$[Q_k, R_k]$ = QR($A_k - \sigma_k I$)
4:	$A_{k+1}$ = $R_k Q_k + \sigma_k I$

实际上 QR 迭代过程还可以进一步的通过偏移量来加快收敛速度。我们知道正常的朴素QR迭代过程就两步: ① 进行 QR 分解，② 交换相乘。如果我们在 QR 分解的时候将对角线上的元素都减去一个常数 $\sigma$，并在交换相乘之后再把这个常数加回来。如此迭代的过程就是带偏移量的 QR 迭代。

整个迭代过程类似左侧的伪代码。其中，$\boldsymbol{A}_{k+1} = \boldsymbol{R}_k \boldsymbol{Q}_k + \sigma_k \boldsymbol{I}$ 仍然与原矩阵相似。

$$ \boldsymbol{A}_{k+1} = (\boldsymbol{Q}_k^T \boldsymbol{Q}_k)\boldsymbol{R}_k \boldsymbol{Q}_k + \sigma_k \boldsymbol{I} = \boldsymbol{Q}_k^T (\boldsymbol{A}_k - \sigma_k \boldsymbol{I})\boldsymbol{Q}_k + \sigma_k \boldsymbol{I} = \boldsymbol{Q}_k^T \boldsymbol{A}_k \boldsymbol{Q}_k $$

只是 $\sigma_k$ 的选择对于迭代过程的影响很大。如果我们选择一个固定的 $\sigma$ 在整个迭代过程中都不变动，那么相当于是先对矩阵 $\boldsymbol{A} - \sigma\boldsymbol{I}$ 进行朴素QR迭代，$\boldsymbol{R}_k \boldsymbol{Q}_k$ 的对角线会收敛到特征值 $\lambda_i - \sigma$。由于朴素的QR迭代收敛之后，对角线上的特征值是按照绝对值大小排序的。所以$\boldsymbol{R}_k \boldsymbol{Q}_k$对角线的元素是按照$|\lambda_i - \sigma|$的大小排序的。最后输出的$\boldsymbol{A}$的特征值也将如此排序，即按照到偏移量的距离排序。

如果我们选择的偏移量刚好就是某个特征值，那么经过一次迭代之后，我们就可以从矩阵的右下角读出改特征值了。在迭代的过程中，矩阵逐渐收敛到上三角形式，对角线上的元素逐渐接近特征值。那么我们可以选择右下角的元素作为每次迭代的偏移量 $\sigma$。这样据说可以加快收敛。我们在 EigenShiftQR 中用成员函数 Iterate 就是按照这种方式实现的。如下图所示，带上 Hessenberg 初始化之后 44 次迭代就可以收敛了。

5. 完

本文本来是想研究一下如何加速QR迭代，写着写着插入了实 Schur 的形式。关于QR迭代的收敛结果我又有了一点新的疑问。后来看到有些材料说还有双位移的QR迭代，据说这个可以得到实Schur的形式。我想如果真是这样，这个应该是QR迭代收敛的最终形式了吧。我们后面会再详细研究一下。

1:	若 \(\max(\|\boldsymbol{A}_{k+1}(i,j) - \boldsymbol{A}_{k}(i,j)\|) ≥ \varepsilon\) 则:
2:	选择一个偏移量 \(\sigma_k\)
3:	\([Q_k, R_k]\) = QR(\(A_k - \sigma_k I\))
4:	\(A_{k+1}\) = \(R_k Q_k + \sigma_k I\)