隐式QR迭代算法
在上一节中,我们提到采用 Hessenberg 形式的矩阵作为迭代初值,可以有效的加快QR算法的收敛速度。 实际上,针对 Hessenberg 形式的矩阵,还有一个隐式Q定理 Implicit Q Theorem,使得我们可以不对迭代矩阵 \(\boldsymbol{A}_k\) 进行 QR 分解,就可以直接计算出 \(\boldsymbol{A}_{k+1}\)。 这样每个迭代过程中,我们就可以避免 \(O(n^3)\) 复杂度的 QR 分解和矩阵乘法运算了。基于该定理的QR算法,就是所谓的隐式QR迭代算法,可以进一步加速。
本文中,我们先研究一下 Hessenberg 矩阵的一些特性,再给出隐式QR算法的实现。
1. 对角分块QR迭代
在研究QR算法的收敛原理的时候,我们介绍过一个定理,上三角矩阵对角线上的元素就是其特征值。 这个定理可以扩展到更一般的情况下:
假设 \(\lambda\) 是 \(\boldsymbol{T}\) 的特征值,对应的特征向量为 \(\boldsymbol{x} = \begin{bmatrix}\boldsymbol{x}_1 \\ \boldsymbol{x}_2\end{bmatrix}\), 那么有 \(\boldsymbol{T}\boldsymbol{x} = \begin{bmatrix} T_{11} & T_{12} \\ 0 & T_{22}\end{bmatrix}\begin{bmatrix}\boldsymbol{x}_1 \\ \boldsymbol{x}_2\end{bmatrix} = \lambda\begin{bmatrix}\boldsymbol{x}_1 \\ \boldsymbol{x}_2\end{bmatrix}\)。若向量 \(\boldsymbol{x}_2 \neq \boldsymbol{0}\),则 \(T_{22}\boldsymbol{x}_2 = \lambda \boldsymbol{x}_2\),所以 \(\lambda \in \lambda(T_{22})\)。若向量 \(\boldsymbol{x}_2 = \boldsymbol{0}\),则 \(T_{11}\boldsymbol{x}_1 = \lambda \boldsymbol{x}_1\),那么 \(\lambda \in \lambda(T_{11})\)。
在上一节中,我们提到上Hessenberg 矩阵是下次对角线以下的元素全为 0 的方阵。 即,在\(n \times n\) 的矩阵中,\(a_{ij} = 0\) 对所有 \(i > j + 1\) 的元素都成立。如果下次对角线上有某个元素为 0 那么根据刚才的定理,我们就可以将一个求 \(n \times n\) 的矩阵的特征值问题, 分解为两个更小规模的矩阵特征值的问题。这样也可以一定程度上减少计算量。比如一个下面的一个 \(4 \times 4\) 的 Hessenberg 矩阵,如果其中 \(a_{32} = 0\), 我们就可以将其转换成两个 \(2 \times 2\) 的子矩阵。
$$ \begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ 0 & a_{32} & a_{33} & a_{34} \\ 0 & 0 & a_{43} & a_{44} \\ \end{bmatrix} \xrightarrow{a_{32} = 0} \left\{ \begin{array}{c} \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} \\ \begin{bmatrix} a_{33} & a_{34} \\ a_{43} & a_{44} \end{bmatrix} \end{array} \right . $$在 QR 迭代过程中,我们完全可以在每次迭代结束之后,扫描一遍次对角线,然后将矩阵划分成若干个子矩阵,分别求解。这样对于大型的矩阵,我们甚至可以进行并行加速。 根据矩阵的实 Schur 分解定理, 原矩阵最终会被分解为若干个 \(1 \times 1\) 或者 \(2 \times 2\) 的子矩阵。对于 \(1 \times 1\) 的子阵,那个唯一的元素就是它的特征值,对于 \(2 \times 2\) 的子阵, 我们可以直接通过一元二次方程公式写出一对共轭的复数特征值。我想这个应该就是 QR 算法收敛的最终形式了吧。
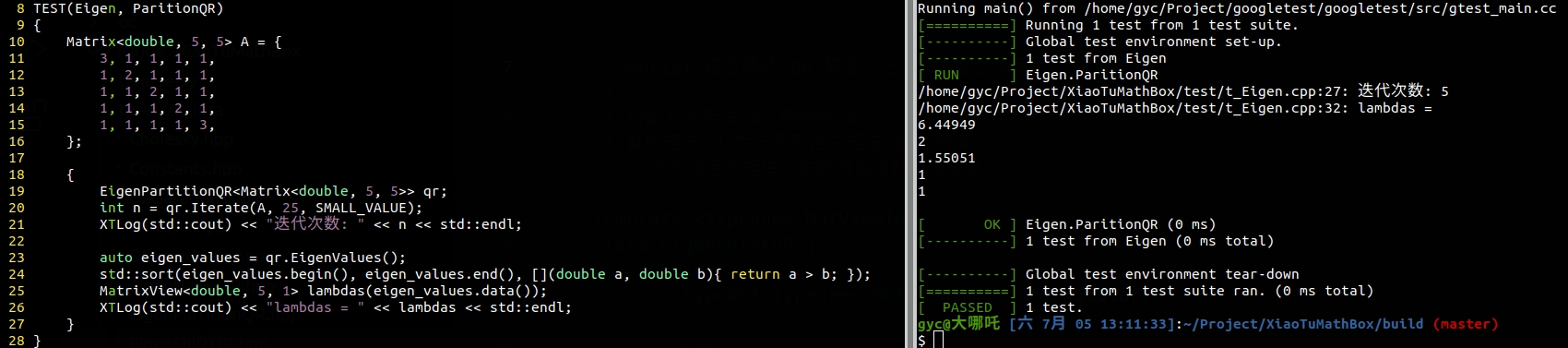
我们在带位移的 QR 算法的基础上,修改了迭代收敛的检查方式,增加对角分块的求解方法,实现了 EigenPartitionQR。 如上图所示,看起来好像收敛的更快了,而且每次迭代的计算量也少了。我满心欢喜的以为,这种方法连复数特征值也能搞定,想要试一把, 于是构造了一个特征多项式为 \(\lambda^5 + 1 = 0\) 的矩阵\(\begin{bmatrix} 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ -1 & 0 & 0 & 0 & 0 \\ \end{bmatrix}\),这个矩阵有 5 个特征值,除了 \(-1\) 之外,剩下的两对都是复数。可是当我将它转换成 Hessenberg 的形式\(\begin{bmatrix} 0 & 0 & 0 & 0 & 1 \\ -1 & 0 & 0 & 0 & 0 \\ 0 &-1 & 0 & 0 & 0 \\ 0 & 0 &-1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ \end{bmatrix}\)之后,不管我进行了多少轮的迭代,它一直都是这个样子没有变过。不收敛呀,看来还得练。

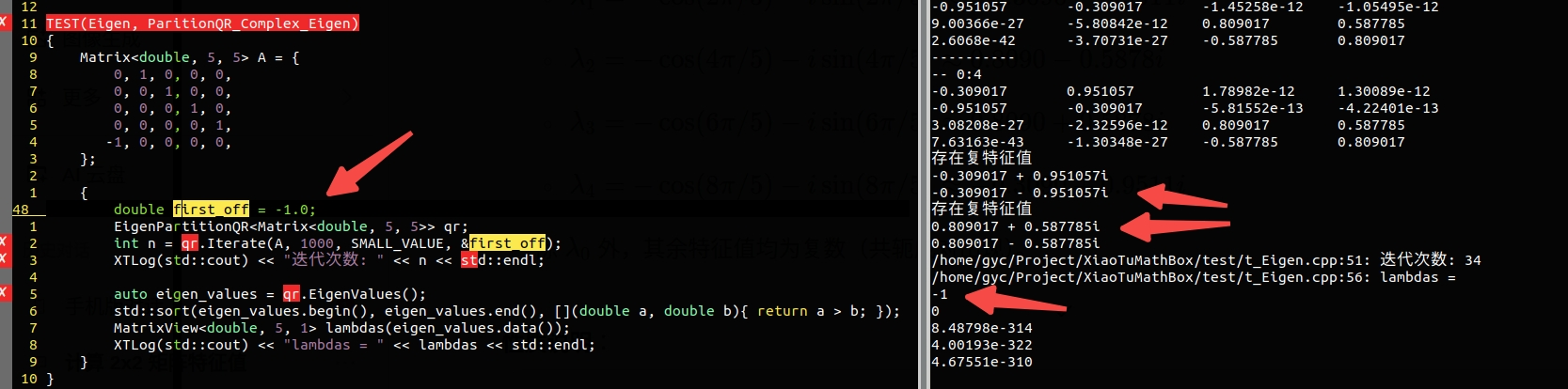
但是,当我指定了第一次迭代时的偏移量为其中一个特征值 -1 之后,就成功求解出了其它两对复数特征值,如下图所示。 看来这个偏移量对于算法是否收敛,以及收敛速度都有重要影响。
3. 隐式 QR 迭代
据说带偏移量的隐式 QR 迭代是目前求解中小型矩阵所有特征值的标准方法,它的理论基础就是下面这个隐式 Q 定理(Implicit Q Theorem)。 基于该定理,我们就可以避免 \(O(n^3)\) 的 QR 分解,直接写出迭代矩阵,所以称为隐式 Implicit。
对于实数域中的一个 \(n\) 维矩阵 \(\boldsymbol{A} \in \mathbb{R}^{n \times n}\)。 假设正交矩阵 \(\boldsymbol{Q}\) 和 \(\boldsymbol{V}\) 分别将 \(\boldsymbol{A}\) 相似变换为 Hessenberg 矩阵 \(\boldsymbol{H} = \boldsymbol{Q}^T\boldsymbol{A}\boldsymbol{Q}\) 和 \(\boldsymbol{G} = \boldsymbol{V}^T\boldsymbol{A}\boldsymbol{V}\)。 令 \(k\) 表示矩阵 \(H\) 下次对角线上为 0 的最小列索引,即满足 \(h_{k+1, k} = 0\) 的最小值。
将正交矩阵展开成列向量的形式,\(\boldsymbol{Q} = \begin{bmatrix} \boldsymbol{q}_1, \cdots, \boldsymbol{q}_n \end{bmatrix}\), \(\boldsymbol{V} = \begin{bmatrix} \boldsymbol{v}_1, \cdots, \boldsymbol{v}_n \end{bmatrix}\)。 如果它们的第一列相同,即,\(\boldsymbol{q}_1 = \boldsymbol{v}_1\),那么 \(\boldsymbol{q}_i = ± \boldsymbol{v}_i\) 对于 \(i = 2, \cdots, k\)都成立。 并且 \(|h_{i, i-1}| = |g_{i, i-1}|\),即矩阵 \(\boldsymbol{H}\) 和 \(\boldsymbol{G}\) 的下次对角线上的元素绝对值相等。 如果 \(k < n\),那么有 \(g_{k+1,k} = 0\)。
上述定理表明,将同一个矩阵相似变换成 Hessenberg 矩阵时,只要保证第一列相同,正交矩阵的其它列只有符号可能不一致。上述定理中关于下次对角线元素是否为 0 的讨论, 主要是在解释,得到的 Hessenberg 矩阵结构上也是一致的,我们可以利用前面讲的对角分块的方法分而治之。 隐式 QR 算法需要先将矩阵预处理为 Hessenberg 形式,它的迭代过程中,会先求得正交矩阵的第一列, 然后通过一系列Givens 变换直接得到 \(\boldsymbol{H}_{k+1}\)。
对于一个 Hessenberg 矩阵 \(\boldsymbol{H}_k\),如果按照先分解再交换相乘的方式进行迭代,那么正交矩阵的第一列,一定与下面矩阵的第一行相同。 下面矩阵是进行 QR 分解时,用来消除元素 \(h_{2,1}\) 的。
$$ G_1 = \begin{bmatrix} h_{1,1} / r & h_{2,1} / r & & & \\ -h_{2,1} / r & h_{1,1} / r & & & \\ & & 1 & & \\ & & & 1 & \\ & & & & 1 \\ \end{bmatrix}, r = \sqrt{h_{1,1}^2 + h_{2,1}^2} $$我们将它相似作用到 \(\boldsymbol{H}_k\) 上,得到的新矩阵就会打破 Hessenberg 的形式,其中元素 \(h_{3,1}\) 可能非零。
$$ G_1\begin{bmatrix} * & * & * & * & * \\ * & * & * & * & * \\ & * & * & * & * \\ & & * & * & * \\ & & & * & * \\ \end{bmatrix}G_1^T = \begin{bmatrix} * & * & * & * & * \\ * & * & * & * & * \\ + & * & * & * & * \\ & & * & * & * \\ & & & * & * \\ \end{bmatrix} $$为了消除该元素,恢复 Hessenberg 的形式,我们可以再用新矩阵的元素 \(h_{2,1}, h_{3,1}\) 构建 Givens 矩阵,再次进行相似变换。
$$ \begin{bmatrix} 1 & & & & \\ & c & s & & \\ & -s & c & & \\ & & & 1 & \\ & & & & 1 \\ \end{bmatrix} \begin{bmatrix} * & * & * & * & * \\ * & * & * & * & * \\ & * & * & * & * \\ & & * & * & * \\ & & & * & * \\ \end{bmatrix}\begin{bmatrix} 1 & & & & \\ & c & -s & & \\ & s & c & & \\ & & & 1 & \\ & & & & 1 \\ \end{bmatrix} = \begin{bmatrix} * & * & * & * & * \\ * & * & * & * & * \\ & * & * & * & * \\ & + & * & * & * \\ & & & * & * \\ \end{bmatrix} $$此时元素 \(h_{4,2}\) 可能变成非零。如此不断构造 Givens 矩阵并进行相似变换,就可以将可能非零元素“赶”出矩阵,恢复 Hessenberg 的形式,直接得到了 \(\boldsymbol{H}_{k+1}\)。 因为整个迭代过程的矩阵稀疏特性,其时间复杂度是 \(O(n^2)\) 的。具体的算法实现参见 EigenImplicitQR。
