QR 分解

我们在介绍方程组的秩时，描述了基和坐标的定义。上一节中，我们在此基础上介绍了线性变换，最后介绍了可以将空间 $\mathbb{V}$ 中的任意一组基转换成正交基的 Gram-Schmidt 算法。实际上利用该算法可以将一个矩阵 $\boldsymbol{A}$ 分解成一个正交矩阵 $\boldsymbol{Q}$ 和一个上三角矩阵$\boldsymbol{R}$，即所谓的 QR 分解 $\boldsymbol{A} = \boldsymbol{Q}\boldsymbol{R}$。如果矩阵 $\boldsymbol{A}$ 可逆，并且矩阵$\boldsymbol{R}$的对角线元素为正数，那么该分解就是惟一的。

上一节最后提到的 Gram-Schmidt 正交化方法实际上就是一个 QR 分解，只是没有把上三角矩阵保存下来。该方法直接从向量的正交基本概念出发，依次构造出标准正交基，简单直观，但是数值稳定性较差。工程上常用 Householder 变换，它本身就是一种正交变换，并且与向量相乘时，有消元的作用。所以可以通过一系列的 Householder 变换将 A 逐步转化为上三角阵。该方法数值稳定。

1. 基于 Gram-Schmidt 的分解

对于一个 $n \times n$ 的矩阵 $\boldsymbol{Q}$，如果它的转置就是它的逆，既 $\boldsymbol{Q}^T = \boldsymbol{Q}^{-1}$，那么该矩阵就是一个正交矩阵。如果我们将正交矩阵看作是一组列向量，那么每个列向量的长度都是 1，并且两两正交。此外，两个正交矩阵的乘积仍然是正交矩阵，正交矩阵左乘到一个列向量上并不会改变向量的长度。 Gram-Schmidt 算法正是基于这些性质逐步构建出正交矩阵 $\boldsymbol{Q}$ 和上三角矩阵 $\boldsymbol{R}$ 的。

假设我们有一个 $n \times n$ 的矩阵 $\boldsymbol{A}$，写成列向量的形式为 $\boldsymbol{A} = \begin{bmatrix} \boldsymbol{\alpha}_1 & \boldsymbol{\alpha}_2 & \boldsymbol{\alpha}_3 & \cdots & \boldsymbol{\alpha}_n \end{bmatrix}$。对其进行 QR 分解之后得到的正交矩阵 $\boldsymbol{Q}$，写成列向量的形式为 $\boldsymbol{Q} = \begin{bmatrix} \boldsymbol{\gamma}_1 & \boldsymbol{\gamma}_2 & \boldsymbol{\gamma}_3 & \cdots & \boldsymbol{\gamma}_n \end{bmatrix}$。有

$$ \begin{bmatrix} \boldsymbol{\alpha}_1 & \boldsymbol{\alpha}_2 & \boldsymbol{\alpha}_3 & \cdots & \boldsymbol{\alpha}_n \end{bmatrix} = \begin{bmatrix} \boldsymbol{\gamma}_1 & \boldsymbol{\gamma}_2 & \boldsymbol{\gamma}_3 & \cdots & \boldsymbol{\gamma}_n \end{bmatrix} \begin{bmatrix} r_{11} & r_{12} & r_{13} & \cdots & r_{1n} \\ & r_{22} & r_{23} & \cdots & r_{2n} \\ & & r_{33} & \cdots & r_{3n} \\ & & & \ddots & \vdots \\ & & & & r_{nn} \end{bmatrix} $$

令 $i = 1$，有 $\boldsymbol{\alpha}_1 = r_{11}\boldsymbol{\gamma}_1$。显然 $r_{11} = \| \boldsymbol{\alpha}_1 \|$，$\boldsymbol{\gamma}_1 = \boldsymbol{\alpha}_1 / \| \boldsymbol{\alpha}_1 \|$。

令 $i = 2$，有 $\boldsymbol{\alpha}_2 = r_{12}\boldsymbol{\gamma}_1 + r_{22}\boldsymbol{\gamma}_2$。因为 $\boldsymbol{Q}$ 是个正交矩阵，所以有$\|\boldsymbol{\gamma}_1\| = 1, \|\boldsymbol{\gamma}_2\| = 1, \boldsymbol{\gamma}_1 \cdot \boldsymbol{\gamma}_2 = 0$。因此有:

$$ \boldsymbol{\gamma}_1 \cdot \boldsymbol{\alpha}_2 = r_{12} \boldsymbol{\gamma}_1 \cdot \boldsymbol{\gamma}_1 + r_{22} \boldsymbol{\gamma}_1 \cdot \boldsymbol{\gamma}_2 = r_{12} $$

根据上式可以得出 $r_{12}$，所以有 $r_{22}\boldsymbol{\gamma}_2 = \boldsymbol{\alpha}_2 - r_{12}\boldsymbol{\gamma}_1$，即， $r_{22} = \| \boldsymbol{\alpha}_2 - r_{12}\boldsymbol{\gamma}_1\|, \boldsymbol{\gamma}_2 = (\boldsymbol{\alpha}_2 - r_{12}\boldsymbol{\gamma}_1) / r_{22}$。

令 $i = 3$，有 $\boldsymbol{\alpha}_3 = r_{13}\boldsymbol{\gamma}_1 + r_{23}\boldsymbol{\gamma}_2 + r_{33}\boldsymbol{\gamma}_3$。利用正交矩阵的性质，可以计算得到 $r_{13}, r_{23}$

$$ \boldsymbol{\gamma}_1 \cdot \boldsymbol{\alpha}_3 = r_{13} \boldsymbol{\gamma}_1 \cdot \boldsymbol{\gamma}_1 + r_{23} \boldsymbol{\gamma}_1 \cdot \boldsymbol{\gamma}_2 + r_{33} \boldsymbol{\gamma}_1 \cdot \boldsymbol{\gamma}_3 = r_{13} $$ $$ \boldsymbol{\gamma}_2 \cdot \boldsymbol{\alpha}_3 = r_{13} \boldsymbol{\gamma}_2 \cdot \boldsymbol{\gamma}_1 + r_{23} \boldsymbol{\gamma}_2 \cdot \boldsymbol{\gamma}_2 + r_{33} \boldsymbol{\gamma}_2 \cdot \boldsymbol{\gamma}_3 = r_{23} $$

根据上式，有 $r_{33}\boldsymbol{\gamma}_3 = \boldsymbol{\alpha}_3 - r_{13} \boldsymbol{\gamma}_2 \cdot \boldsymbol{\gamma}_1 - r_{23} \boldsymbol{\gamma}_2 \cdot \boldsymbol{\gamma}_2$。那么 $r_{33} = \|\boldsymbol{\alpha}_3 - r_{13} \boldsymbol{\gamma}_2 \cdot \boldsymbol{\gamma}_1 - r_{23} \boldsymbol{\gamma}_2 \cdot \boldsymbol{\gamma}_2\|$, $\boldsymbol{\gamma}_3 = (\boldsymbol{\alpha}_3 - r_{13} \boldsymbol{\gamma}_2 \cdot \boldsymbol{\gamma}_1 - r_{23} \boldsymbol{\gamma}_2 \cdot \boldsymbol{\gamma}_2) / r_{33}$。

实际上上述过程正是我们在上一节最后提到的 Gram-Schmidt 正交化方法。对于 $2 < k ≤ n$，我们都可以通过 $\boldsymbol{\alpha}_k - \sum_{i=2}^{k} \frac{\boldsymbol{\alpha}_k \cdot \boldsymbol{\beta}_i}{\boldsymbol{\beta}_i\boldsymbol{\beta}_i}\boldsymbol{\beta}_i$ 构造出 $\boldsymbol{\beta}_k$ 与 $\boldsymbol{\beta}_1 \cdots \boldsymbol{\beta}_{k-1}$ 都正交。如果我们再对 $M_2$ 中的每个向量单位化，即，令 $\boldsymbol{\gamma}_i = \boldsymbol{\beta}_i / |\boldsymbol{\beta}_i|$，那么就可以得到一组单位正交基 $M_3 = \left\{ \boldsymbol{\gamma}_1, \cdots, \boldsymbol{\gamma}_n\right\}$。这正式 QR 分解中的正交矩阵。上三角矩阵中对角线上的元素 $r_{ii}$ 则是向量 $\boldsymbol{\beta}_i$ 的模长。其余元素 $r_{ij} = \boldsymbol{\gamma}_i \cdot \boldsymbol{\alpha}_j$。实现参见例程QR_GramSchmidt。

Gram-Schmidt 算法十分简洁，但不幸的是它的数值稳定性不怎么样，在工程上很少使用。基于 Householder 变换的 QR 分解算法，能在计算过程中较好地控制舍入误差的传播，非常适合用于大规模的矩阵分解。

2. Householder 矩阵

Householder 变换是一种正交变换，它通过构造一个镜像反射矩阵，也就是所谓的 Householder 矩阵 $\boldsymbol{H}$，在保持向量长度不变的同时，将一个向量 $\boldsymbol{x}$映射到另一个指定方向的向量 $\boldsymbol{y} = \boldsymbol{H}\boldsymbol{x}$。通过合理的选择 Householder 向量 $\boldsymbol{v}$，可以将原向量 $\boldsymbol{x}$ 中的指定元素变成 0。

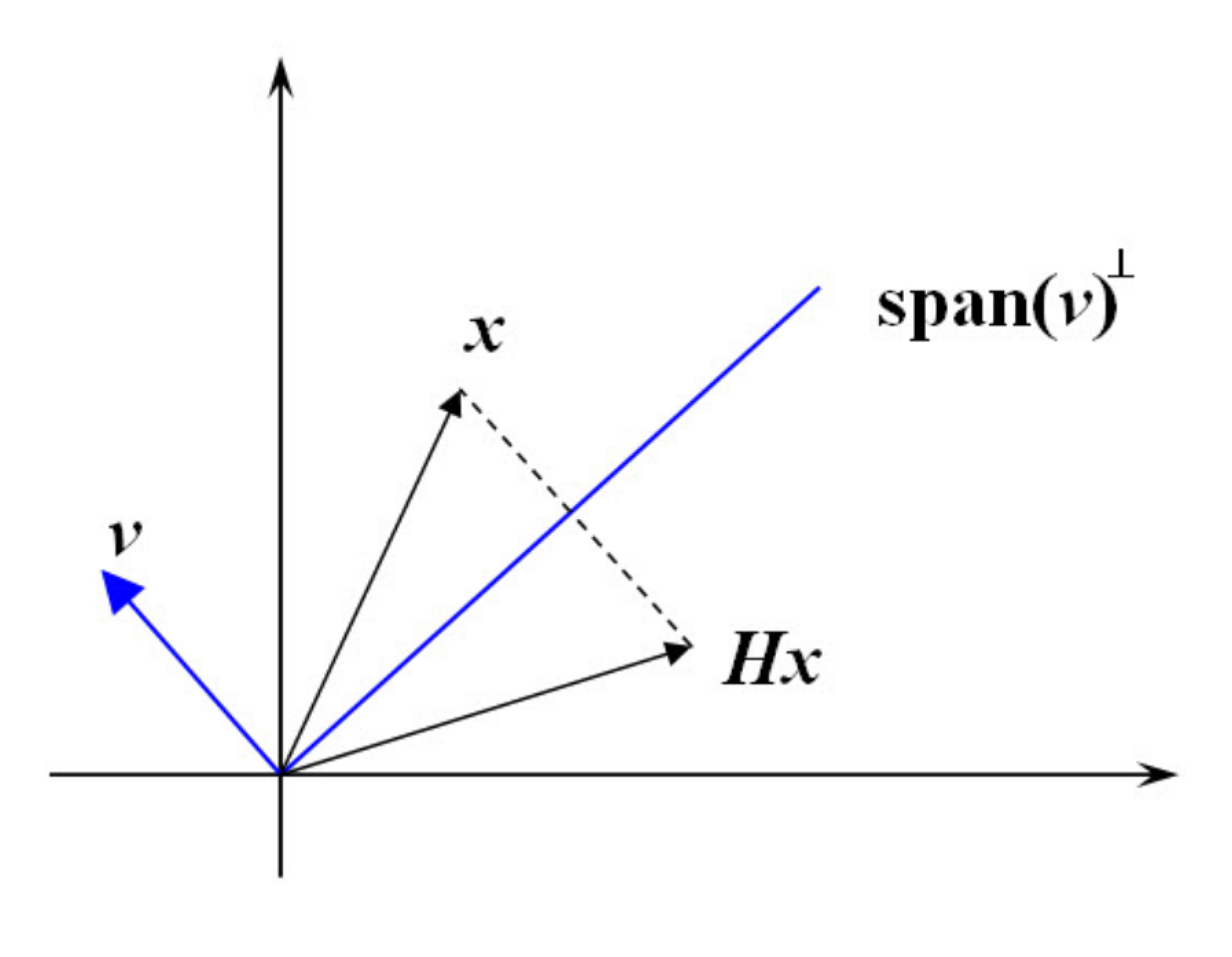
给定一个非零向量 $\boldsymbol{v}$，可以按照如下的方式构造 Householder 矩阵: $$ \boldsymbol{H} = \boldsymbol{I} - \frac{2 \boldsymbol{v}\boldsymbol{v}^T}{\| \boldsymbol{v} \|^2} $$ 其中，$\boldsymbol{I}$ 是一个单位矩阵，$\boldsymbol{v}\boldsymbol{v}^T$ 是向量 $\boldsymbol{v}$ 的外积，$\| \boldsymbol{v} \|$则是 $\boldsymbol{v}$ 的长度。矩阵 $\boldsymbol{H}$ 是正交的，即 $\boldsymbol{H}^T = \boldsymbol{H}^{-1}$；也是对称的，即 $\boldsymbol{H}^T = \boldsymbol{H}$；也是对合的，即$\boldsymbol{H}^{-1} = \boldsymbol{H}$。Householder 矩阵的几何意义是，将向量 $\boldsymbol{x}$ 关于一个垂直于 $\boldsymbol{v}$ 的超平面 $\text{span}(\boldsymbol{v})^{\perp}$ 的镜面反射$\boldsymbol{H}\boldsymbol{x}$。

由于 $\boldsymbol{H}$ 本身就是正交的，所以我们可以不断的左乘不同的 Householder 矩阵，将目标矩阵 $\boldsymbol{A}$ 上三角化，即，$\boldsymbol{A} = \boldsymbol{H}_k \cdots \boldsymbol{H}_2 \boldsymbol{H}_1 \boldsymbol{R}$，其中 $\boldsymbol{H}_k \cdots \boldsymbol{H}_2 \boldsymbol{H}_1$ 是一系列的 Householder 矩阵，也就是 QR 分解中的那个矩阵 $\boldsymbol{Q}$，$\boldsymbol{R}$ 则是那个上三角矩阵。

假设 $\boldsymbol{x}, \boldsymbol{y}$ 是空间 $\mathbb{F}^n$ 中两个非零向量，如果它们的长度相等，即 $\|\boldsymbol{x}\| = \| \boldsymbol{y} \|$，那么就一定存在一个矩阵 $\boldsymbol{H}$，使得 $\boldsymbol{y} = \boldsymbol{H}\boldsymbol{x}$。因为两个向量的模长相等，所以有 $\boldsymbol{x}^T\boldsymbol{x} = \boldsymbol{y}^T\boldsymbol{y}$，并且 $\boldsymbol{x}^T\boldsymbol{y} = \boldsymbol{y}^T\boldsymbol{x}$。因此，存在如下关系: $$ \| \boldsymbol{x} - \boldsymbol{y} \|^2 = (\boldsymbol{x} - \boldsymbol{y})^T(\boldsymbol{x} - \boldsymbol{y}) = \boldsymbol{x}^T\boldsymbol{x} + \boldsymbol{y}^T\boldsymbol{y} - (\boldsymbol{x}^T\boldsymbol{y} + \boldsymbol{y}^T\boldsymbol{x}) = 2(\boldsymbol{x}^T\boldsymbol{x} - \boldsymbol{y}^T\boldsymbol{x}) $$ 令 $\boldsymbol{v} = \boldsymbol{x} - \boldsymbol{y}$，根据 Householder 矩阵的定义有 $$ \boldsymbol{H}(\boldsymbol{v}) \boldsymbol{x} = \boldsymbol{x} - \frac{2 (\boldsymbol{x} - \boldsymbol{y})(\boldsymbol{x} - \boldsymbol{y})^T \boldsymbol{x}}{\| \boldsymbol{x} - \boldsymbol{y} \|^2} = \boldsymbol{x} - \frac{2 (\boldsymbol{x} - \boldsymbol{y})(\boldsymbol{x}^\boldsymbol{x} - \boldsymbol{y}^T\boldsymbol{x})} {2(\boldsymbol{x}^T\boldsymbol{x} - \boldsymbol{y}^T\boldsymbol{x})} = \boldsymbol{y} $$ 所以存在 Householder 矩阵 $\boldsymbol{H}(\boldsymbol{v})$ 使得 $\boldsymbol{y} = \boldsymbol{H}(\boldsymbol{v}) \boldsymbol{x}$。向量 $\boldsymbol{v}$ 被称为 Householder 向量。假设 $\boldsymbol{x} = \begin{bmatrix} x_1 & \cdots & x_n \end{bmatrix}^T$， $\boldsymbol{y} = \begin{bmatrix} \alpha & \cdots & 0 \end{bmatrix}^T$，其中 $\alpha = \pm \| \boldsymbol{x} \|$。我们可以直接构造出 Householder 向量 $\boldsymbol{v} = \begin{bmatrix} x_1 - \alpha & \cdots & x_n \end{bmatrix}$，使得经 Householder 矩阵映射后的向量除第一个元素外的所有元素都变成零。这一特性可以拿来对矩阵进行 QR 分解。在工程应用中，为了控制舍入误差，我们应当尽量避免两个相近的数做减法运算，所以，通常取 $\alpha = -\text{sign}(x_1) \| \boldsymbol{x} \|$。我们在单元测试 TEST(QR, HouseholderMatrix) 中给出了一种只保留指定元素的实现。

3. 基于 Householder 的分解

基于 Householder 变换的 QR 分解的基本思想就是不断的构造 Householder 矩阵对目标矩阵进行消元，只保留上三角区域的元素。假设有一个 $m \times n$ 的矩阵 $\boldsymbol{A}$，对其进行 QR 分解之后的正交矩阵是 $m \times m$ 的，上三角矩阵则是 $m \times n$ 的。

我们将 $\boldsymbol{A} = \begin{bmatrix} a_{11} & \cdots & a_{1n} \\ \vdots & \ddots & \vdots \\ a_{m1} & \cdots & a_{mn} \end{bmatrix}$，写成列向量的形式， $\boldsymbol{A} = \begin{bmatrix} \boldsymbol{\alpha}_1 & \cdots & \boldsymbol{\alpha}_n \end{bmatrix}$，其中 $\boldsymbol{\alpha}_i = \begin{bmatrix} a_{1i} \\ \vdots \\ a_{mi} \end{bmatrix}$。对于 $\boldsymbol{\alpha}_1$ 有矩阵 $\boldsymbol{H}_1$使得 $\boldsymbol{H}_1 \boldsymbol{\alpha}_1 = \begin{bmatrix} r_{11} \\ \vdots \\ 0 \end{bmatrix}$。那么 $$ \boldsymbol{H}_1 \boldsymbol{A} = \left[ \begin{array}{c|c} r_{11} & \begin{matrix} r_{12} & \cdots & r_{1n} \end{matrix} \\ \hline \begin{matrix} 0 \\ \vdots \\ 0 \end{matrix} & \tilde{\boldsymbol{A}}_2 \end{array}\right] $$ 其中 $\tilde{\boldsymbol{A}}_2$ 是一个 $(m-1) \times (n-1)$ 的矩阵，同样的方式，我们可以构造 $(m-1) \times (m-1)$ 的矩阵 $\tilde{\boldsymbol{H}}_2$ 对 $\tilde{\boldsymbol{A}}_2$ 消元仅保留第一列第一行的元素，即 $$ \tilde{\boldsymbol{H}}_2 \tilde{\boldsymbol{A}}_2 = \left[ \begin{array}{c|c} r_{22} & \begin{matrix} r_{23} & \cdots & r_{2n} \end{matrix} \\ \hline \begin{matrix} 0 \\ \vdots \\ 0 \end{matrix} & \tilde{\boldsymbol{A}}_3 \end{array}\right] $$ 构造 $\boldsymbol{H}_2 = \begin{bmatrix} 1 & \boldsymbol{0} \\ \boldsymbol{0} & \tilde{\boldsymbol{H}}_2 \end{bmatrix}$，那么有 $$ \boldsymbol{H}_2 \boldsymbol{H}_1 \boldsymbol{A} = \left[ \begin{array}{c|c} \begin{matrix} r_{11} & r_{12} \\ 0 & r_{22} \end{matrix} & \begin{matrix} r_{13} & \cdots & r_{1n} \\ r_{23} & \cdots & r_{2n} \end{matrix} \\ \hline \begin{matrix} 0 & 0 \\ \vdots & \vdots \\ 0 & 0 \end{matrix} & \tilde{\boldsymbol{A}}_3 \end{array}\right] $$ 不断重复上述过程，我们需要构造出 $m - 1$ 个 Householder 矩阵，才能最终将矩阵$\boldsymbol{A}$ 上三角化，即 $\boldsymbol{H}_{m-1} \cdots \boldsymbol{H}_2 \boldsymbol{H}_1\boldsymbol{A} = \boldsymbol{R} = \begin{bmatrix} r_{11} & r_{12} & \cdots & r_{1n} \\ & r_{22} & \cdots & r_{2n} \\ & & \ddots & \vdots \\ & & & r_{mn} \end{bmatrix}$。

令 $\boldsymbol{Q} = (\boldsymbol{H}_{m-1} \cdots \boldsymbol{H}_2\boldsymbol{H}_1)^{-1} = \boldsymbol{H}_1\boldsymbol{H}_2 \cdots \boldsymbol{H}_{m-1}$，则有对矩阵 $\boldsymbol{A}$ 的 QR 分解 $\boldsymbol{A} = \boldsymbol{Q}\boldsymbol{R}$。实现参见例程QR_Householder。

4. Givens 旋转矩阵

在实数域$\mathbb{R}$中，我们成如下形式的矩阵为 Givens 矩阵，其中 $c = \cos(\theta), s = \sin(\theta)$。它实际上是单位矩阵，将其中四个元素替换成 $c$ 或 $±s$。即，$\boldsymbol{G}_{i,i} = c$,$\boldsymbol{G}_{i,j} = s$, $\boldsymbol{G}_{j,i} = -s$, $\boldsymbol{G}_{j,j} = c$。显然该矩阵是正交的，并且其行列式为 1，即，$\det(\boldsymbol{G}(i,j,\theta)) = 1$。

$$ \boldsymbol{G}(i,j,\theta) = \begin{bmatrix} 1 & & & & & & \\ & \ddots & & & & & \\ & & c & \cdots & s & & \\ & & \vdots & \ddots & \vdots & & \\ & & -s & \cdots & c & & \\ & & & & & \ddots & \\ & & & & & & 1 \\ \end{bmatrix} \in \mathbb{R}^{n \times n}, \qquad (i ≤ j) $$

如果 $n = 2$，它就是一个 2 维空间下的旋转矩阵，将它左乘到一个向量上，相当于将该向量逆时针旋转了 $\theta$ 角。$n > 2$ 时，相当于在一个 $n$ 维的空间中，选定了 $i,j$ 轴确定的平面作逆时针的旋转运动，将它左乘到一个向量上，只会改变其中第$i,j$的元素，其它元素均保持不变。

参考 Givens 矩阵的几何意义，给定索引$i,j$，我们只需要计算出这两个元素构成矢量的方向角，就能够构造出一个 Givens 矩阵消除索引$j$的元素。具体的构造过程可以参见类 Givens。由于 Givens 矩阵左乘到一个矩阵上，只会改变 $i,j$ 两行，而右乘只会改变 $i,j$ 两列。如果只更新对应的两行或者两列，计算量会小很多，是 $O(n)$ 的计算复杂度。所以，我们也在类 Givens 中提供了一些成员函数，用于以各种姿势作用到一个矩阵上。

5. 基于 Givens 的分解

由于 Givens 矩阵是正交的，我们可以不断地选择合理元素索引 $i,j$ 以及旋转角度 $\theta$，让指定矩阵中第 $i$ 行 $j$ 列的元素变换成 0。将多个 Givens 矩阵串乘起来，就可以得到一个上三角矩阵，如此就可以实现矩阵的 QR 分解。比如下面的一个 $4 \times 4$ 的矩阵 $\boldsymbol{A}$，我们先后使用 3 次 Givens 变换，就可以消去第一列中后三个元素。于是有 $\boldsymbol{R} = \boldsymbol{G}_{3,4}\boldsymbol{G}_{2,4}\boldsymbol{G}_{2,3} \boldsymbol{G}_{1,4}\boldsymbol{G}_{1,3}\boldsymbol{G}_{1,2}\boldsymbol{A}$，所以有QR分解 $\boldsymbol{A} = \boldsymbol{G}_{1,2}^T\boldsymbol{G}_{1,3}^T\boldsymbol{G}_{1,4}^T\boldsymbol{G}_{2,3}^T\boldsymbol{G}_{2,4}^T\boldsymbol{G}_{3,4}^T\boldsymbol{R}$。

$$ \boldsymbol{A} = \begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} \\ \end{bmatrix} \xrightarrow{\boldsymbol{G}(1, 2)} \begin{bmatrix} * & * & * & * \\ 0 & * & * & * \\ a_{31} & a_{32} & a_{33} & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} \\ \end{bmatrix} \xrightarrow{\boldsymbol{G}(1, 3)} \begin{bmatrix} * & * & * & * \\ 0 & * & * & * \\ 0 & * & * & * \\ a_{41} & a_{42} & a_{43} & a_{44} \\ \end{bmatrix} \xrightarrow{\boldsymbol{G}(1, 4)} \begin{bmatrix} * & * & * & * \\ 0 & * & * & * \\ 0 & * & * & * \\ 0 & * & * & * \\ \end{bmatrix} $$