临接表描述的图
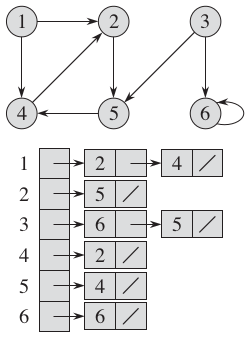
图\(G = (V, E)\)的临接表形式是由\(|V|\)个临界列表构成的。对于每个\(u \in V\),其临接表\(Adj[u]\)中记录了所有与该点有连接的边\((u, v) \in E\),其中\(v\)是\(u\)的临接节点。 如右图所示,是一个有向图的临接表示例。
上面的描述中并没有明确临接形式,而实际上根据图的类型不同临接形式也有很多变化。从数学上,根据边的形式可以把图分为有向图和无向图。对于有向图而言,临接具有两个方面的意义: 从\(u\)点出发的边和到达\(u\)点的边。有时我们还会不加区分的处理这两种临接,这就相当于是无向图。
本文中,我们以C++模板的形式实现临接表描述的图。首先定义节点和边两个构成图的基本要素,再对这两者进行封装,提供图的曾删改操作。
1. 图的基本要素
下面的代码片段分别是边和节点的定义。我希望将图设计成比较通用的容器,尽可能的提供关于图的各种运算,让用户使用时不必过于关注图的拓扑结构细节。所以,我们为这两个基本要素定义了字段key, 用于存储用户真正感兴趣的数据。这点也是考虑到了未来加权图的扩展。
|
|
对于边,我们还为之定义了两个GNode的指针from和to。在有向图中,from指示边的起点,to则指示边的终点。在无向图中,它们的字面意思就不存在了,我们将不加区分的看待两个指针。 对于节点,我们定义了两个GEdge类型的指针数组。在有向图中,inEdges表示所有指向本节点的边,称之为入边;而outEdges则记录了所有从本节点出发的边,称之为出边。 在无向图中,我们也不再区分这两个数组的字面意义,它们都是本节点的边。
需要强调的是,虽然在无向图中,我们不区分from, to以及inEdges, outEdges的字面意思。但是inEdges中记录的所有边的to字段,和outEdges中所有边的from字段都指向节点本身。
下面是边的各个构造函数,它们无非是根据参数列表构建边的对象而已。值得关注的是,其中第3,4行中定义的拷贝构造函数。它在初始化列表中,为from和to赋予了空的初值。 这样做主要是考虑到,单纯的修改边的拓扑关系并不足以体现整个图的改变,我们还需要对应的修改节点的入边和出边列表,这一操作更适合放在它们的上层封装Graph中实现。
GEdge()
: from(NULL), to(NULL) { }
GEdge(EdgeType const & data)
: from(NULL), to(NULL), key(data) { }
GEdge(GNode<NodeType, EdgeType> *f, GNode<NodeType, EdgeType> *t)
: from(f), to(t) { }
GEdge(GNode<NodeType, EdgeType> *f, GNode<NodeType, EdgeType> *t, EdgeType const & data)
: from(f), to(t), key(data) { }
下面是GEdge中重载的操作符。出于和拷贝构造函数相同的考虑,下面的第1到4行中的拷贝赋值操作符中,只完成了字段key的拷贝,而不处理拓扑关系。行5,6的操作符为GEdge提供了一种隐式的数据类型变换, 将GEdge类型转换为EdgeType类型的变量。
GEdge & operator = (EdgeType const &data) {
key = data;
return *this;
}
& operator EdgeType() { return key; }
& operator const EdgeType() const { return key; }
边其实没有什么曾删的需求,它无非是记录了存在联系的两个节点而已。对于一个节点而言,我们常常会添加或者删除一条边。下面左右两边的代码分别给出了添加和删除入边和出边的函数。 在这四个函数中,我们首先检查输入的参数是合法的,再修改入边或者出边列表。同样的,我们在GNode中并不修改GEdge的内容,而是将之保留到Graph中实现。
|
|
我们也为GNode提供了拷贝赋值操作符,和用于隐式的将GNode类型转换为NodeType类型的操作符,其实现形式和思想与GEdge一致不再赘述。我们并没有为GEdge和GNode提供析构函数, 因为这两个类并不申请内存,它们只是通过指针记录下整个图的拓扑关系。边和节点的内存将在Graph中管理。
2. 图的实现
下面的代码片段是Graph的部分定义。我们用GNode的指针数组nodes记录图中所有的节点对象,GEdge的指针数组edges记录所有边对象。通过num_nodes和num_edges接口可以查看图中的节点数和边数。
template <class NodeType, class EdgeType>
class Graph {
public:
int num_nodes() const { return nodes.size(); }
int num_edges() const { return edges.size(); }
public:
DataArray<GNode<NodeType, EdgeType> *> nodes;
DataArray<GEdge<NodeType, EdgeType> *> edges;
};
下面的函数完成了向Graph对象中添加边的操作。该函数有三个参数,from和to分别是边的两个节点指针,key则是边的键值数据。该函数正常运行的话,申请一个GEdge的对象, 并通过这三个参数完成对象的构造,如第7行代码所示。在第8,9行中,分别在两个节点中添加新增的出边和入边信息。第13行用成员edges记录新构造的边对象。 此外,在函数的一开始,我们需要确认边的两个节点在图中。
GEdge<NodeType, EdgeType> *add_edge(GNode<NodeType, EdgeType> *from, GNode<NodeType, EdgeType> *to, EdgeType const & key) {
if (NULL == nodes.find(from))
return NULL;
if (NULL == nodes.find(to))
return NULL;
GEdge<NodeType, EdgeType> *edge = new GEdge<NodeType, EdgeType>(from, to, key);
from->add_outedge(edge);
to->add_inedge(edge);
edges.push(edge);
return edge;
}
我们并不提供以GEdge的指针或者引用形式为参数的add_edge重载,这是为了保证Graph能够完全负责它的节点和边的内存管理。如果提供了这样的重载,意味着在Graph控制之外存在了一个边对象, 这是不符合我们的意愿的。
下面是删除一条边的函数。我们以GEdge的指针为参数,在函数的一开始检查边edge属于Graph。通过检查之后,我们先在两个节点的出边列表和入边列表中删除edge的记录。 然后从Graph的edges列表中将之移除。最后释放边对象的内存并返回。
bool remove_edge(GEdge<NodeType, EdgeType> *edge) {
int idx = edges.find_idx(edge);
if (-1 == idx)
return false;
edge->from->remove_outedge(edge);
edge->to->remove_inedge(edge);
edges.remove(idx);
delete edge;
return true;
}
下面是添加节点的函数,只是以参数key构建一个GNode的对象并将之记录在nodes列表中。同样的,我们不提供以GNode类型数据为参数的add_node重载。
GNode<NodeType, EdgeType> *add_node(NodeType const & key) {
GNode<NodeType, EdgeType> *re = new GNode<NodeType, EdgeType>(key);
nodes.push(re);
return re;
}
下面是从Graph中移除一个节点的函数。首先检查输入的参数node属于Graph,如果属于则从nodes列表中将之移除
bool remove_node(GNode<NodeType, EdgeType> *node) {
int idx = nodes.find_idx(node);
if (-1 == idx)
return false;
nodes.remove(idx);
接下来我们遍历该节点的所有边,将之从Graph中删除。
int num_out = node->degree_out();
for (int i = 0; i < num_out; i++) {
GEdge<NodeType, EdgeType> *edge = node->outEdges[i];
remove_edge(edge);
}
int num_in = node->degree_in();
for (int i = 0; i < num_in; i++) {
GEdge<NodeType, EdgeType> *edge = node->inEdges[i];
remove_edge(edge);
}
最后,释放node的内存并返回。
delete node;
return true;
}
因为在Graph需要负责其节点和边的对象内存管理,所以我们还需要为之提供一个析构函数,用于在Graph声明周期结束的时候,指导其释放申请的内存。在该函数中,我们依次遍历ndoes和edges列表, 释放列表中记录的对象的内存。
~Graph() {
int no = nodes.size();
int ne = edges.size();
for (int i = 0; i < no; i++)
delete nodes[i];
for (int i = 0; i < ne; i++)
delete edges[i];
}
3. 完
本文中,我们用C++模板提供了临接表形式的图。虽然分别定义了边和节点两个基本要素的类GEdge和GNode,但是它们相互之间不能修改数据,只维护必要的拓扑关系。 而图的边和节点对象的内存则是由Graph维护。
