第三章：有Point Feet的平面双足机器人模型

本章介绍点足平面双足机器人的行走和奔跑运动的动力学模型。假设机器人由有质量的刚性连杆构成， 它们之间通过刚性、无摩擦的旋转关节连接，在一个平面内形成一个开运动链(open kinematic chain)。 更进一步的，我们假设这个机器人有两个被称为“腿(leg)”的完全相同的子链，连接在一点上称之为“臀(hip)”。 此外，机器人身上还可以有称为“躯干(torso)”、“臂(arm)”甚至是“尾(tail)”的子链，但它们不是必须的。 由于每条腿的末端都是一个点，这样一来，机器人要么没有脚，要么是踮着脚尖走路。 左图就是满足假设的一个典型的机器人，我们特意将其画成一个人的形状。

我们假定所有的运动都是在纵向平面(Sagittal plane)上的。 行走运动是单脚支撑和双脚支撑交替出现的过程，而奔跑则是单脚支撑和腾空交替出现的过程。始终保持脚的末端与地面接触， 躯干、臂、尾巴等其余的连杆部分都是在空中的。爬行(crawling)、筋斗(tumbling)、跨越(skipping)、蹦跳(hopping)、 舞蹈(dancing)以及臂越(brachiation)等运动都不是我们的研究内容。

针对行走和奔跑运动过程中交替出现的各种不同的状态，我们需要分别建立数学模型：描述单脚支撑期动力学特性的微分方程； 描述腾空期动力学特性的微分方程；以及脚末端碰撞地面时的动力学模型。在这里， 地面(也被称为行走或者奔跑平面)被认为是平滑的(smooth)，垂直于重力场的。也就是说地面是平的，而不是一个斜坡，也不是凹凸不平的。

与地面的碰撞过程可以柔顺的(compliant)也可以是非弹性的(inelastic)^注。 柔性的碰撞过程通常是用非线性的弹簧阻尼(nonlinear spring-dampers)模型^{[ 24, 149,194]}描述的。 对于一般的行走平面而言，比如说地板，并不像蹦蹦床那样，碰撞过程或者说是碰撞模型的transient phase是非常短暂的。 其微分方程十分复杂，充分的对其建模将极大的提高仿真的复杂度和行走奔跑步态的分析难度。 而且，为柔性碰撞模型辨识合适的物理参数本身都是一个极具挑战的科学问题。为了简化分析难度， 本书中控制器的设计和分析都是建立在刚性碰撞模型基础之上的。刚性碰撞模型^{[ 74, 208 ]}将整个碰撞过程看作是一个瞬间发生的能量转换。 碰撞力则通过冲量(impulses)建模，允许在机器人的速度上形成一个不连续点或者说是跳跃点。这一瞬间可以通过一个参数进行描述， 这一参数被称为连续余度(remaining continuous)或者是碰撞常数(constant during the impact)。 所以，行走和奔跑的动力学模型就是一个混合的(hybrid)模型，由连续的动力学过程和碰撞事件发生后的重新初始化规则构成(consisting of continuous dynamics and a reinitialization rule at the impact event)。

3.1 为什么是点足?

双足机器人系统复杂度的一个主要来源就是系统驱动度(the degree of actuation of the system)。 更准确的说是系统的欠驱动(underactuation)程度。在本章中，我们假设双腿末端是一个点，这样一来支撑腿的末端是不可能有驱动的。 因此，在单脚支撑期中整个系统就是欠驱动的而不是全驱动的(所谓的全驱动是指，机器人的每个关节以及与地面的接触点都是有驱动控制的。 a control at each joint and at the contact point with the ground)。在奔跑步态的腾空期，整个系统也是欠驱动的。

有人可能认为，真实的机器人是有脚的，所以点足模型虽然在数学上是有意义的，但是不能够适用于真实的机器人。 我们希望本书的第三部分，关于有脚的行走方式和有驱动的脚踝的讨论，可以减轻这样的疑惑。有人拿人类的标准来衡量双足机器人的行走效果， 目前的这些平板足的机器人还有待提高。而且，这类机器人的行走步态还需要有一个弯曲脚趾的过程。目前而言，这类技术还是受限的， 尤其是在欠驱动的情况下^注， 我们并不能够以轨迹跟踪以及准静态稳定判据(quasi-static stability criterion,比如说ZMP)的控制理念来处理弯曲脚趾的过程。

一个拟人的行走步态至少有以下几个阶段，支撑脚平放在地面上的全驱动期(a fully actuated phase where the stance foot is flat on the ground)， 紧接着支撑脚后跟离开地面支撑脚趾弯曲的欠驱动期(an underactuated phase where the stance foot heel lift from the ground and the stance foot rotates about the toe)，以及一个交换支撑腿时的双脚支撑期，这一阶段也可以包含脚后跟着地并转动的动作(optionally, heel strike and heel roll could also be included)，这又是一个欠驱动的过程。对于这两个欠驱动期，点接触的行走模型是一种对整个行走过程的建模方法， 相比与目前平板足行走步态而言，点足模型是一种更拟人的模型。因为点足模型是一种更简单的模型，它应用了最新的反馈控制设计、动态稳定性分析方法， 而这种动态的方法比准静态的方法更适合。

3.2 机器人、步态和碰撞假设

接下来的内容都是对第一章中的专有名词的解释。单腿支撑期single support或者摆动腿过程swing phase是指只有一条腿与地面接触的时期。 对应的双腿支撑期double support是指两条腿都与地面接触的时期。下图1(1)和图1(2)分别示意了非点足式机器人和点足式行走的各个阶段。 当只有一条腿与地面接触的时候，那么该腿就被称为支撑腿stance leg，另一条腿则被称为摆动腿swing leg。 行走walking可以定义为单脚支撑期与双脚支撑期交替出现的过程，在这个过程中要求机器人质心水平分量的值是一个严格的单调函数， 并且在发生碰撞的时候摆动腿总是在支撑腿之前的。这样的描述就暗含着碰撞瞬间脚不打滑的假设。脚的末端，既是没有一个被称为脚的连杆， 我们也将之称为“脚”foot。

图1(1) 非点足式机器人行走的各个阶段。其中(a)和(b)描述了单脚支撑阶段，也称作摆动腿阶段。 而(c)则描述了双脚支撑期。如果机器人的所有关节都是受控的并且脚底不会打滑，那么对比机器人的自由度以及关节驱动器的数量，有如下结论： (a)是全驱动的(fully actuated)，(b)是欠驱动的(underactuated),(c)则是过驱动的(overactuated)。	图1(2) 点足式机器人行走的各个阶段。图(a)是单脚支撑期，图(b)则是双脚支撑期。 如果机器人的所有关节都是受控的并且脚底不打滑，那么(a)是欠驱动的，(b)是过驱动的。

当机器人与地面之间没有接触点，并且其质心坐标的水平分量是一个严格的单调函数时，我们称机器人的这种状态为腾空flight phase， 有时也称之为弹道运动ballistic motion。相比于支撑期，机器人在腾空期具有额外的两个自由度。在支撑期， 机器人的姿态可以完全由各个的值来决定。而在腾空期中，额外增加了机器人质心在纵向平面(sagittal plane)中位置的两个分量。 奔跑running可以定义为单脚支撑、腾空、单脚触地状态的交替出现的过程。并且碰撞时触地的腿不是上一个周期中的支撑腿，而是摆动腿。 需要注意的是，在腾空过程中摆动腿的概念具有一定的歧义，因此特指上次单脚支撑期中的那条摆动腿。

在这些概念的基础上，我们可以列出如下的假设列表，用来描述机器人模型、行走和奔跑步态，以及碰撞模型。

Point Feet机器人假设

行走步态假设

特别的，假设HGW5和HGW6意味着碰撞瞬间两条腿的角色发生互换。所以行走过程不会是一个，固定一条腿另一条腿在支撑腿前后往复运动的过程。 步态的对称特性是简单行走运动的自然特征，而不是应用本书中理论的必要条件。比如说，我们可以分析一个因为受伤而引起的病态行走模型， 这种病态的行走方式就是一种非对称的运动。在本书中提到的方法基础之上，做一些小的扩展，就可以用来分析一个膝关节是被动的(passive，或者说是假肢)， 另一个膝关节是受驱动的步态。

跑动步态假设

刚体碰撞模型假设

当摆动腿接触到地面时就会发生碰撞。碰撞过程常用两个刚体接触的模型来描述。目前已经提出了有很多种碰撞模型[12,23,24,124,174]， 这些模型都可以归结为，在行走平面上根据碰撞之前摆动腿的速度和位置来计算碰撞之后的速度。 这里参考文献[124]描述行走和奔跑步态的碰撞过程。两个过程本质上是一样的，在一些方面有些差异，记录如下：

为了帮助理解最后一个假设，我们来看下面这个二阶时不变系统在\(t=t_0 > 0\)时刻的冲击响应。 $$ \begin{equation}\label{f1} \ddot{x}(t) + a\dot{x}(t) + bx(t) = c \delta (t-t_0) \end{equation} $$ 其中，\(\delta (t)\)为单位脉冲函数，\(a,b,c \in \mathbb{R}\)。对公式(\(\ref{f1}\))一次积分 $$ \begin{align}\label{f2} \dot{x}(t) & = \dot{x}(0) + \int_0^t (-a\dot{x}(\tau) - bx(\tau) + c\delta(\tau - t_0)) d\tau \\ & = \dot{x}(0) - ax(t) + ax(0) - \int_0^t bx(\tau)d\tau + c\varepsilon(t - t_0) \end{align} $$ 其中，\(\varepsilon(t)\)是单位阶跃函数，因此\(\dot{x}(t)\)在\(t = t_0\)处不连续。对公式(\(\ref{f2}\))再次积分有： $$ \begin{align}\label{f3} x(t) & = x(0) + \int_0^t (\dot{x}(0) - ax(\delta) + ax(0)) d\delta - \int_0^t \left(\int_0^{\delta} bx(\tau)d\tau - c\varepsilon(\delta - t_0)\right) d\delta \\ & = x(0) + \left(\dot{x}(0) + ax(0)\right)t - \int_0^t ax(\delta)d\delta - \int_0^t \int_0^{\delta} bx(\tau)d\tau d\delta + c·(t - t_0)\varepsilon(t-t_0) \end{align} $$ 称\(x\)和\(\dot{x}\)在\(t_0^+\)(\(t_0^-\))时刻的值为函数在\(t_0\)时刻的右(左)极限。称\(x(t_0^-)\)和\(\dot{x}(t_0^-)\)为碰撞之前的位置和速度， \(x(t_0^+)\)和\(\dot{x}(t_0^+)\)为碰撞之后的位置和速度。公式(\(\ref{f3}\))中\(x(t_0^+) - x(t_0^-) = 0\)，意味着在碰撞过程中，位置是连续的。 从公式(\(\ref{f2}\))中可以推出\(\dot{x}(t_0^+) - \dot{x}(t_0^-) = c\)，意味着在碰撞之后速度发生了跳变。

3.3 一些符号表示

本章主要是推到行走和奔跑的动力学模型，单脚支撑期的广义坐标用符号\((q_s;\dot{q}_s)\)表示，而腾空期的广义坐标用符号\((q_f;\dot{q}_f)\)表示。 在同时讲述行走和奔跑的章节中区分这两种不同的状态是有必要的。在本书的其它章节中，如果只讲行走就没必要区分单脚支撑期和腾空期了， 我们就可以用符号\((q;\dot{q}_s)\)来表示其广义坐标。

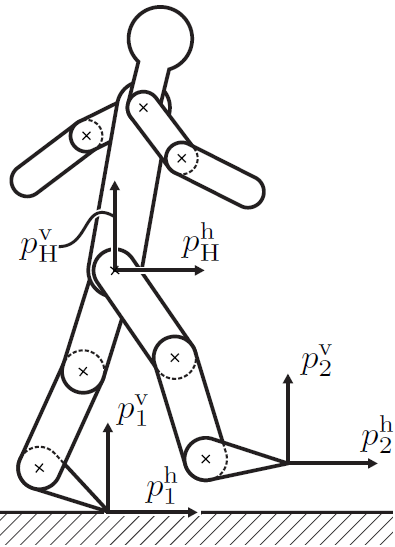
一般的，机器人上的一个点(或者是其质点)在惯性坐标系下的坐标为\(p = (p^h,p^v)\)。下图描述了一些需要特别关注的点和力。 分别是支撑腿和摆动腿的末端，记为\(p_1, p_2\)，臀部的位置\(p_H\)，质心的位置\(p_{cm}\)。在支撑期中，这些点都可以表达为广义坐标\(q_s\)的连续函数。

图2 一些关键位置和力。本图中标记了对于任何满足HR1-HR5的机器人的脚末端、臀部、质心的位置， 以及可能的脚末端受力情况。(a)和(b)图描述的是行走步态中的点标记，(c)则是奔跑步态中的标记。

对于奔跑机器人的腾空期，完全可以从支撑期的一系列广义坐标系开始结合机器人上质心的位置和速度构建一组广义坐标系(It is nature and always possible, though not required, to construct generalized coordinates by starting with a set of generalized coordinates for the stance phase and then appending the Cartesian position and velocity of a single point on the robot(or its center of mass).)。 此时，为了强调质点坐标是两个独立的变量，我们在图2(c)中用"x-y"坐标表示一个点。特别的，腾空期的广义坐标表示为\(q_f = (q_s; x_{cm}; y_{cm})\)。

坐标符号中的分号";"表示构成一个列向量，比如\((q_s; x_{cm}; y_{cm})\)表示： $$ \left[ \begin{matrix} q_s \\ x_{cm} \\ y_{cm} \end{matrix} \right] $$ 用这种形式来替代\((q_s', x_{cm}, y_{cm})'\)可以减少标记矩阵转置的上角标，使得表达更清晰。多变量函数的输入参数仍然是用逗号','分隔的。

3.4 行走的动力学模型

本部分提供了一个满足机器人模型假设HR1-HR5、步态假设HGW1-HGW7，以及碰撞模型假设的HI1-HI7的双足机器人行走步态的数学模型。 假设机器人在惯性参考系下运动，并且需要考虑重力。假设HGW7中要求行走面是一个平面，因此不失一般性的我们可以认为地面高度为0。 如图2(a)所示，\(p_1=(p_1^h;p_1^v)\)表示腿1末端在惯性参考系下的位置坐标， \(p_2=(p_2^h,p_2^v)\)表示腿2末端的坐标。

3.4.1 摆动腿模型

摆动腿模型描述的是一个固定的开链结构。根据假设HGW5，行走步态是一种对称的运动，而那条腿是固定在地面上的与分析没有影响， 所以我们不加区分的用腿1来标记支撑腿。我们在下一节讨论碰撞模型时考虑腿1和腿2角色互换的问题。

令\(\mathcal{Q}_s\)为机器人的\(N\)维运动空间(Configuration Space)，把支撑腿末端看作是一个支点， \(q_s := (q_1;\cdots;q_N) \in \mathcal{Q}_s\)表示广义坐标系(generalized coordinates)。 我们就可以通过拉格朗日(Lagrange)方法建立动力学模型(参考附录B.4)。 拉格朗日方法先计算每个连杆的动能(kinetic energy)和势能(potential energy)， 再将它们分别求和得到系统的总动能\(K_s\)和总势能\(V_s\)， 最后建立拉格朗日方程(Lagrangian)：

$$ \begin{equation} \mathcal{L}_s(q_s, \dot{q_s}) := K_s(q_s, \dot{q_s}) - V_s(q_s) \end{equation} $$ 应用拉格朗日方法，可以得到如下形式的摆动腿动力学模型(参考附录B.4.4)： $$ \begin{equation}\label{f3.8} D_s(q_s)\ddot{q_s} + C_s(q_s, \dot{q_s})\dot{q_s} + G_s(q_s) = B_s(q_s)u \end{equation} $$ 式中\(D_s\)为惯性矩阵，\(C_s\)是科氏力矩阵(Coriolis Matrix)，\(G_s\)是重力向量，\(B_s\)为表示关节力矩的广义力。 \(u := (u_1;\cdots;u_{N-1}) \in \mathbb{R}^{(N-1)}\)表示各个关节的力矩，支撑腿与地面之间是没有驱动力矩的。 令\(\theta^{rel}_i(q_s)\)表示\(i^{th}\)执行关节的相对角度(relative angle)，那么矩阵\(B_s\)可以通过如下公式计算得出： $$ \begin{equation} B_s(q_s) := \left(\frac{\partial}{\partial{q_s}}\left[\begin{matrix} \theta^{rel}_1 \\ \vdots \\ \theta^{rel}_{N-1} \end{matrix}\right]\right)^T \end{equation} $$ 在HR6的假设下，\(B_s\)可以表示为： $$ \begin{equation} B_s = \left[\begin{matrix} I_{N-1 \times N-1} \\ 0_{1 \times N-1} \end{matrix}\right] \end{equation} $$ 因此，对于每一个\(q_s \in \mathcal{Q}_s\)，都有： $$ \begin{equation} rank [B_s(q_s)] = N - 1 \end{equation} $$ 其动力学模型还可以写成状态空间的形式： $$ \begin{equation} \label{f3.13} \begin{array}{lcl} \dot{x} & = & \left[\begin{matrix} \dot{q_s} \\ D^{-1}_s(q_s)[-C_s(q_s,\dot{q_s}) - G_s(q_s) + B_s(q_s)u] \end{matrix}\right] \\ & =: & f_s(x) + g_s(x)u \end{array} \end{equation} $$ 其中\(x := (q_s; \dot{q_s})\)为系统状态。模型的状态空间用\(\mathcal{X}_s = T\mathcal{Q}_s\)表示。对于每一个\(x \in T\mathcal{Q}_s\)， \(g_s(x)\)都是一个\(2N \times (N - 1)\)的矩阵，其第\(i\)列用符号\(g_{s_{i·}}\)表示。对于\(T\mathcal{Q}_s\)的坐标\((q_s;\dot{q}_s)\)而言， \(g_s\)与\(\dot{q}_s\)无关，所以有时我们会用符号\(g_s(q_s)\)来代替\(g_s(x)\)。

It is clear that not all configurations of the model are physically compatible with our notion of the single support phase of walking. 比如说对于支撑腿末端，机器人上所有点都应当在行走平面之上，对于一个类人的行走步态，膝关节是不能够伸长的(hyperextend)。此外，还有一些运动学的约束， 例如，支撑腿末端相当于一个支点，作用在支撑腿末端的力一定不能大于最大静摩擦力，而且反作用力一定是个正数。这些问题将在设计控制器的章节中讨论。

3.4.2 碰撞模型

碰撞模型将在腿末端引入作用反力，因此需要对机器人建立一个不固定的(unpinned)或者说是一个具有\(N+2\)自由度的模型。 我们对单腿支撑期的模型做如下扩展，记摆动腿模型的广义坐标系为\(q_s\)，\(p_e = (p^h_e, p^v_e)\)为机器人上某一固定点(可以是质心)的笛卡尔坐标表示， 我们用\(q_e = (q_s;p_e)\)表示碰撞模型下的广义坐标。利用拉格朗日方法建模得到： $$ \begin{equation} D_e(q_e)\ddot{q_e} + C_e(q_e, \dot{q_e})\dot{q_e} + G_e(q_e) = B_e(q_e)u + \delta F_{ext} \end{equation} $$ 其中\(\delta F_{ext}\)为摆动腿落地瞬间地面对机器人产生的作用力矢量。假设HI5说明了这些作用力是脉冲形式的(impulsive)，因此用符号\(\delta F_{ext}\)标记。 根据碰撞假设HI1~HI7，对碰撞过程的积分有 ^[124]： $$ \begin{equation}\label{f3.15} D_e(q_e^+)\dot{q_e^+} - D_e(q_e-)\dot{q_e^-} = F_{ext} \end{equation} $$ 其中\(F_{ext} = \int_{t^-}^{t^+}\delta F_{ext}(\tau)d\tau\)是对冲击力的积分效果， \(\dot{q}_e^-\)是碰撞瞬间之前的速度，\(\dot{q}_e^+\)是碰撞瞬间之后的速度。 假设HI7要求碰撞过程中位置不发生改变，因此有\(q_e^+ = q_e^-\)。实质上式(\(\ref{f3.15}\))描述了动量守恒 ^[124]。在后续文章中进行控制分析的时候，我们再详细解释这里提及的固定点。

---

根据定义，碰撞前的速度由摆动腿模型确定。碰撞前\(p_e^-\)可以通过\(p_e^- = \mathcal{\Upsilon}(q_s^-)\)得到。因此有： $$ \begin{equation} q_e^- = \left[\begin{matrix} q_s^- \\ \mathcal{\Upsilon}_e(q_s^-) \end{matrix}\right] = \left[\begin{matrix} I_{N \times N} \\ \frac{\partial}{\partial{q_s}}\mathcal{\Upsilon}_e(q_s^-) \end{matrix}\right]\dot{q_s}^- \end{equation} $$

根据假设HI4，摆动腿(leg-2)末端的作用力为\(F_{ext}\)，令\(p_2(q_e)\)为惯性坐标系下摆动腿的位置，根据虚功原理有： $$ \begin{equation} F_{ext} = E_2(q_e^-)^TF_2 \end{equation} $$ 其中，\(E_2(q_e) = \frac{\partial}{\partial{q_e}}p_2(q_e)\)并且\(F_2 = (F_2^T; F_2^N)\)为作用在摆动腿末端的力矢量。 因为\(p_2(q_e) = p_e + \mathcal{\Upsilon}_2(q_s)\)，故\(E_2 = [\partial\mathcal{\Upsilon}_2(q_s)/\partial q_s, I_{2\times 2}]\)。

式(\(\ref{f3.15}\))有\(N+2\)个方程，\(N+4\)个未知数(\(\dot{q_e^+}, F_2^T, F_2^N\))。根据假设HI3有 $$ \begin{equation}\label{f3.19} E_2(q_e^-)\dot{q_e^+} = 0 \end{equation} $$ 联立式(\(\ref{f3.15}, \ref{f3.19}\))有： $$ \begin{equation}\label{f3.20} \left[\begin{matrix}D_e(q_e^-) & -E_2(q_e^-)^T \\ E_2(q_e^-) & 0_{2 \times 2} \end{matrix}\right] \left[\begin{matrix}\dot{q_e^+} \\ F_2 \end{matrix}\right] = \left[\begin{matrix}D_e(q_e^-)\dot{q_e^-} \\ 0_{2 \times 1} \end{matrix} \right] \end{equation} $$ 可以证明上式左端的矩阵是可逆的，因此有： $$ \begin{equation}\label{f3.22} \left[\begin{matrix}\dot{q_e^+} \\ F_2 \end{matrix}\right] = \left[\begin{matrix}\bar{\Delta}_{\dot{q_e}}(q_s^-) \\ \Delta_{F_2}(q_s^-)\end{matrix}\right]\dot{q^-_s} \end{equation} $$ 其中： $$ \begin{equation}\label{f3.23} \Delta_{F_2} = -(E_2D_e^{-1}E_2^T)^{-1}E_2\left[\begin{matrix}I_{N \times N} \\ \frac{\partial}{\partial q_s}\mathcal{\Upsilon}_e \end{matrix}\right] \end{equation} $$ $$ \begin{equation}\label{f3.24} \bar{\Delta}_{\dot{q_e}} = D_e^{-1}E_2^T\Delta_{F_2} + \left[\begin{matrix}I_{N\times N} \\ \frac{\partial}{\partial q_s}\mathcal{\Upsilon}_e\end{matrix}\right] \end{equation} $$ 我们可以用式(\(\ref{f3.22}\))对式(\(\ref{f3.13}\))reinitialize。因为我们假设行走步态是对称的，所以就不用建立两个摆动腿模型了。 只需要在碰撞的时候切换两条腿的角色，即relabeling。relabeling的工作是建立一个矩阵\(R\)把碰撞前各关节的广义坐标系映射到碰撞后的广义坐标系。 因为连续两次碰撞后，两条腿的角色就有切换回来了，所以有\(RR = I\)，即\(R\)是一个循环矩阵(circular matrix)。 我们把relabeling操作用算子\(\Delta\)来表示，那么碰撞前后状态向量之间存在关系： $$ \begin{equation} x^+ = \Delta(x^-) \end{equation} $$ 其中，\(x^+ := (q^+_s; \dot{q^+_s}), x^- := (q^-_s; \dot{q^-_s})\)，并且： $$ \begin{equation} \Delta(x^-) := \left[\begin{matrix} \Delta_{q_s}q^-_s \\ \Delta_{\dot{q_s}}(q^-_s)\dot{q^-_s} \end{matrix}\right], \Delta_{q_s} := R, \Delta_{\dot{q_s}}(q^-_s) := [\begin{matrix}R & 0_{N \times 2}\end{matrix}]\bar{\Delta}_{\dot{q_e}}(q_s^-) \end{equation} $$

根据假设HGW2和HGW4，我们有如下约束：碰撞时摆动腿受法向力为正\(F_2^N > 0\)，切向力不超过最大静摩擦力\(|F_2^T| ≤ μ_sF_2^N\)， 其中\(μ\)为静摩擦系数。支撑腿抬起时不会产生作用力，令\(p_1^h(q^e);p_1^v(q^e)\)为碰撞前支撑腿的坐标，那么有约束： $$ \begin{equation} \dot{p_1^v} = \frac{\partial}{\partial q_e}p_1^v(q_e^-)\dot{q_e^+} \end{equation} $$ 式中\(\dot{q_e^+}\)用公式(\(\ref{f3.22}\))计算得到。每当碰撞发生时，都必须判定上述三个约束条件是否满足。

3.4.3 行走混合模型(Hybrid Model of Walking)

一个完整的行走模型是由摆动腿模型和碰撞模型两部分构成的，它描述了一个具有冲击响应的系统(a system with impulse effects)。 我们记任意时刻摆动腿的左极限和右极限分别为\(x^-(t) := \lim_{\tau \nearrow t}x(\tau), x^+(t) := \lim_{\tau \searrow t}x(\tau)\)。行走模型可以写为： $$ \begin{equation}\label{f3.30} \Sigma : \begin{cases} \dot{x} = f_s(x) + g_s(x)u & x^- \notin \mathcal{S} \\ x^+ = \Delta(x^-) & x^- \in \mathcal{S} \end{cases} \end{equation} $$ 其中\(\mathcal{S}\)为碰撞点集合(按:原文为switching set，本意是说碰撞时切换两腿的角色，这实际上就是碰撞点)： $$ \begin{equation}\label{f3.31} \mathcal{S} := \{(q_s, \dot{q_s}) \in \mathcal{TQ}_s | p_2^v(q) = 0, p_2^h(q) > 0 \} \end{equation} $$ 求解过程参考下图

图 行走混合模型

在4.1节中将详细介绍模型解的数学意义。机器人的步伐step就是机器人从双脚支撑期开始，经过单脚支撑期，到达下一个双脚支撑其结束，其中只包含一次碰撞的过程，是公式(\(\ref{f3.30}\))的解。 行走Walking则是一个步伐的序列。

3.4.4 一些影响角动量的因素

3.4.4.1 重力在行走中的作用

在对机器人进行建模时，我们假设腿的末端点是不会有驱动力矩的。So, what causes the robot to rotate about the support leg end and thus advance forward in a step? The answer is gravity.令\(\sigma_1\)为机器人关于支撑腿末端的角动量。根据角动量守恒定律有：在一点的角动量的微分等于外力作用在该点力矩的和。 因为电机输出的力矩实际上是机器人的内力，它们不影响角动量守恒，因此，作用的外力只有重力。 $$ \begin{equation} \label{f3.32} \dot{\sigma_1} = \begin{cases} g_0m_{tot}(p_{cm}^h - p_1^h), & 顺时针约定 \\ -g_0m_{tot}(p_{cm}^h - p_1^h), & 逆时针约定 \end{cases} \end{equation} $$ 其中\(g_0\)为重力加速度常数，\(m_{tot}\)为机器人总质量，\(p_{cm}^h\)为机器人质心的水平位置，\(p_1^h\)为支撑腿末端点的水平位置。 如此看来机器人模型就好像是一个被动双足行走机器人(passive bipedal walker)[ 58, 59, 153].

那么机器人上各个关节的执行器都起什么作用呢？执行器直接影响机器人的姿态，进而可以改变质心位置，这就改变了重力的力臂。 另外，机器人的姿态对于碰撞时的能量损失也有巨大的影响[ 125]， 也决定了双腿末端的约束是否能够满足。

3.4.4.2 Momentum Transfer at Impact

令\(\sigma_1^-\)为碰撞前关于支撑脚的角动量，\(\sigma_2^-\)为碰撞前关于摆动脚的角动量。根据the principle of moment transfer有： $$ \begin{equation} \sigma_2^- = \sigma_1^- + (p^-_1 - p^-_2)\wedge m_{tot}\dot{p^-_{cm}} \end{equation} $$

在碰撞过程中，由于碰撞力是作用在摆动腿末端点的，所以碰撞前后\(\sigma_2\)是没有改变的，即： $$ \sigma_2^+ = \sigma_2^- $$ 考虑到碰撞后需要切换坐标系，两条腿的角色将发生变化，所以切换后有： $$ \begin{equation} \sigma_1^+ = \sigma_1^- + (p^-_1 - p^-_2)\wedge m_{tot}\dot{p^-_{cm}} \end{equation} $$ 如果机器人行走在一个水平面上，那么有 $$ \begin{equation} \label{f3.36} \dot{\sigma_1^+} = \begin{cases} \sigma_1^- + L_s\wedge m_{tot}\dot{p^{v-}_{cm}}, & 顺时针约定 \\ \sigma_1^- - L_s\wedge m_{tot}\dot{p^{v-}_{cm}}, & 逆时针约定 \end{cases} \end{equation} $$ 其中，\(L_s\)为步长，\(\dot{p^{v-}_{cm}}\)为碰撞前质心在竖直方向的速度。

3.4.5 The MPFL-Normal Form

本节目的是把公式(\(\ref{f3.8}, \ref{f3.13}\))用一个标准型表示，这是一种基于partial feedback linearization的思想[187, 220]。

对于一个广义坐标系\(q_s = (q_b; q_N)\)，其中\(q_b = (q_1;\cdots;q_{N-1})\)是体坐标系(body coordinates)集， \(q_N\)描述了机器人在惯性坐标系下的朝向。

根据424页的命题B.8，\(q_N\)是一个cyclic坐标系，意味着式(\(\ref{f3.8}\))中的惯性矩阵与\(q_N\)没有关系，即\(D_s(q_s) = D_s(q_b)\)。 因为\(\frac{\partial \theta_i^{rel}}{\partial q_N} \equiv 0, 1 ≤ i ≤ N-1\)，因此式(\(\ref{f3.8}\))中的输入矩阵具有如下形式： $$ B_s(q_s) = \left[\begin{matrix}B_1(q_b) \\ 0 \end{matrix}\right] $$ 其中\(B_1(q_b)\)是一个可逆的方阵，对于所有的\((q_b;q_N) \in \mathcal{Q}_s\)都成立。

令\(\Omega(q_s, \dot{q_s}) := C_s(q_s, \dot{q_s})\dot{q_s} + G_s(q_s)\)对公式(\(\ref{f3.8}\))拆分，有： $$ \begin{equation} \begin{matrix} D_{11}(q_b)\ddot{q_b} + D_{12}(q_b)\ddot{q_N} + \Omega_1(q_s, \dot{q_s}) & = & B_1(q_b)u \\ D_{21}(q_b)\ddot{q_b} + D_{22}(q_b)\ddot{q_N} + \Omega_2(q_s, \dot{q_s}) & = & 0 \end{matrix} \end{equation} $$ 因为\(D_s\)是正定的，所以\(D_{11}, D_{22}\)是正定的、可逆的。令： $$ \begin{cases} \bar{D} & := & D_{11} - D_{12}D_{22}^{-1}D_{21} \\ J^{norm} & := & D_{22}^-1D_{21} \\ \bar{\Omega}_1 & := & \Omega_1 - D_{12}D_{22}^{-1}\Omega_2 \\ \bar{\Omega}_2 & := & - D_{22}^{-1}\Omega_2 \end{cases} $$ 对于regular static state feedback： $$ \begin{equation} \label{f3.42} u = B_1^{-1}(q_b)\left(\bar{D}(q_b)v + \bar{\Omega}_1(q_s, \dot{q_s}) \right) \end{equation} $$ 可以解得： $$ \begin{equation}\label{f3.43} \begin{cases} \ddot{q_b} & = & v \\ \ddot{q_N} & = & \bar{\Omega}_2 - J^{norm}(q_b) v \end{cases} \end{equation} $$ 以上被称为partial feedback linearization normal form。其中\(D_{22} = d_{NN}\)是一个标量。对于状态变量\(x := (q_s, \dot{q_s})\)，有： $$ \begin{equation}\label{f3.44} \dot{x} = \left[\begin{matrix} \dot{q_s} \\ v \\ \bar{\Omega}_2 - J^{norm}(q_b) v\end{matrix}\right] =: \tilde{f}_s(x) + \tilde{g}_s(x)v \end{equation} $$ 上式就是将反馈(\(\ref{f3.42}\))应用到式(\(\ref{f3.13}\))得到的结果。式(\(\ref{f3.44}\))的优势在于不需要计算惯性矩阵\(D_s\)的逆。

关于\(q_N\)的广义共轭动量(generalized momentum conjugate to \(q_N\))为： \(\bar{\sigma}_N = \frac{\partial \mathcal{L}_s}{\partial \dot{q}_N}\)。有： $$ \begin{equation} \label{f3.47} \bar{\sigma}_N = \sum_{k=1}^{N} d_{N,k}(q_1, \cdots, q_{N-1})\dot{q_k} \end{equation} $$ 因为支撑腿末端点没有驱动力，并且\(q_N\)is cyclic： $$ \begin{equation} \label{f3.48} \dot{\bar{\sigma}}_N = - \frac{\partial V_s}{\partial q_N}(q) \end{equation} $$ 结合式(\(\ref{f3.43},\ref{f3.48}\))有 $$ \begin{equation}\label{f3.49} \begin{cases} \ddot{q_b} & = & v \\ \ddot{q_N} & = & \frac{\bar{\sigma}_N}{d_{N,N}(q_b)} - J^{norm}(q_b) \dot{q_b} \\ \dot{\bar{\sigma}}_N & = & - \frac{\partial V_s}{\partial q_N}(q_b, q_N) \end{cases} \end{equation} $$ 这被称为Mixed-Partial-Feedback-Linearized(MPFL) normal form。定义： $$ \begin{equation} \bar{\omega}_s := \left[\begin{matrix} \dot{q_b} \\ \bar{\sigma}_N \end{matrix} \right] = \begin{matrix}\underbrace{\left[\begin{matrix} I_{N-1 \times N-1} & 0_{N-1 \times 1} \\ d_{N,N}(q_b)J^{norm}(q_b) & d_{N,N}(q_b) \end{matrix} \right]} & \left[\begin{matrix} \dot{q_b} \\ \dot{q_N} \end{matrix} \right] \\ M(q_b) & \end{matrix} \end{equation} $$ 对于状态向量\(\tilde{x} := (q_s; \bar{\omega}_s)\)，有状态方程： $$ \begin{equation}\label{f3.52} \dot{\tilde{x}} = \left[\begin{matrix} \dot{q_b} \\ \frac{\bar{\sigma}_N}{d_{N,N}(q_b)} - J^{norm}(q_b) \dot{q_b} \\ v \\ - \frac{\partial V_s}{\partial q_N}(q_b, q_N) \end{matrix}\right] =: \tilde{f}_s(\tilde{x}) + \tilde{g}_s(\tilde{x})v \end{equation} $$