第十三章：FastSLAM算法

现在我们将注意力转向SLAM的粒子滤波方法。在本书的之前的一些章节中我们已经介绍了粒子滤波器。我们注意到粒子滤波器在一些最有效的机器人算法中占据着核心的地位。这就产生了一个问题，粒子滤波器是否可以用于SLAM问题。不幸的是，粒子滤波器受限于空间维度，高斯类算法状态估计问题的维度还在线性和二次方之间，而粒子滤波器则是指数级的。直接将粒子滤波器应用于SLAM问题注定会，因为描述地图时所需的大量变量而失效。

本章中算法建立在SLAM问题的一个重要特性上，到目前为止我们还没有讨论它。特别的，在已知关联度的完全SLAM问题中，给定机器人位姿，在地图中任意两个不相交的特征集合之间，存在着条件独立性。换句话说，如果有条神谕告诉我们真正的机器人路径，我们就可以不依赖于其它特征，来估计所有的特征位置。只有当不确定机器人位姿的时候，这些估计的依赖性才存在。这一结构性的观察，将使得我们有可能使用一种称为Rao-Blackwellized particle filter(简称为RB滤波器)的粒子滤波器来解决SLAM问题。RB滤波器使用粒子集合来表示一些变量的后验概率，同时用高斯或者其它参数化的概率密度来表示剩下的所有变量。

FastSLAM使用粒子滤波器来估计机器人的路径。我们可以看到，对于每个粒子，它们各自的地图误差都是条件独立的。因此建图问题可以差分为很多子问题，每个问题都对应着地图中的一个特征。 FastSLAM使用EKF估计这些地图特征的位置，但对各个特征所使用的EKF都是相对低维的。这与之前章节中讨论的SLAM算法有着本质的不同，之前的章节中都是用一个高斯函数还估计所有状态的联合分布。

基本的算法可以在特征数量的对数时间中完成。因此，FastSLAM算法的效率高于朴素的EKF实现以及很多其它变型。FastSLAM的关键优势在于，可以基于每个粒子做出数据关联决策。如此一来，滤波器维护了多个数据关联的后验分布，不仅仅是对一个关联的估计。这点与我们目前讨论的所有SLAM算法形成了鲜明的对比，那些算法在同一个时间只跟踪一个数据关联。实际上通过对数据关联进行采样，FastSLAM完全是对后验概率的近似，不仅仅是数据关联度的极大似然估计。实践告诉我们，同时跟踪多个数据关联度，使得FastSLAM算法在数据关联度问题的鲁棒性上，明显由于那些基于增量极大似然数据关联度的算法。

FastSLAM相比于其它SLAM算法的另一个优势在于，粒子滤波器可以处理非线性的机器人运动模型，而之前的技术只是通过线性方程对这些模型做出了近似。当运动学是高度非线性，或者位姿不确定度相对较高的时候，这点很重要。

粒子滤波器的使用缔造了FastSLAM的不一般的地位，它既可以解决完全SLAM问题，也可以搞定在线SLAM问题。我们将会看到，FastSLAM所用的公式是计算完全路径的后验概率的，只有当完全路径提供了特征位置的条件独立性时才成立。但是因为粒子滤波器在一个时间点估计一个位姿，FastSLAM实际上是一个在线的算法。因此它也解决了在线的SLAM问题。在我们目前所讨论的算法中，FastSLAM时唯一一种解决两个问题的算法。

本章描述了一些FastSLAM算法的实例。FastSLAM 1.0时最初的FastSLAM算法，在概念上很简单而且很容易实现。在特殊的情况下，FastSLAM 1.0的粒子滤波器不能高效的生成样本。 FastSLAM 2.0算法通过一种改进的建议分布克服了这一问题，但是实现上就要复杂很多，而且其数学推导也复杂了。这两种FastSLAM算法使用的都是基于特征的传感器模型。 FastSLAM的应用在距离传感器上，得到了一种在占用栅格地图上解决SLAM问题的算法。对于所有的算法，本章提供估计数据关联变量的技术。

13.1 基本算法

如图13.1所示，描述了基本的FastSLAM算法中的粒子形式。每个粒子都含有一个机器人位姿估计，记为$x_t^[k]$，以及描述地图中每个特征$m_j$的期望$\mu_{j,t}^{[k]}$和方差$\Sigma_{j,t}^{[k]}$的卡尔曼滤波器集合。其中$[k]$是粒子的索引。按照惯例，所有的粒子数量记为$M$。

图 13.1.FastSLAM中的粒子。它由一个路径估计和一个对各个特征位置及其协方差的估计器集合构成。

基本的FastSLAM算法的更新步骤如图13.2所示。除却更新过程中的各种细节，其主要循环过程与第四章中讨论的粒子滤波器大体上相同。在初始阶段设计了检索在$t-1$时刻用来表示后验概率的粒子，并使用概率运动模型生成$t$时刻的机器人位姿样本。接下来的步骤中，根据观测到的特征使用标准的EKF更新公式更新EKF。这个更新过程并不是粒子滤波器的一部分，但是在FastSLAM中学习一幅地图是必须的。最后的阶段，涉及到计算重要性权重，并用于粒子的重采样。

图 13.2.FastSLAM算法的基本步骤。

我们现在将更细致的研究每个步骤，并推导它们在SLAM问题中的基本数学特性。需要注意，这里的推导假定FastSLAM解决的是完全SLAM问题，而不是在线问题。但是，在本章接下来的内容中就会看到，FastSLAM是这两种问题的解决方案。每个粒子可以看作是路径空间上，用于解决完全SLAM问题的一个样本。但是更新只需要最近的位姿。因此FastSLAM可以像一个滤波器那样运行。

13.2 SLAM后验概率的因式分解

FastSLAM的核心数学思想来自于，完全SLAM的后验概率$p(y_{1:t} | z_{1:t}, u_{1:t})$可以因式分解成如下的形式: $$ \begin{equation}\label{f1} p(y_{1:t} | z_{1:t}, u_{1:t}, c_{1:t}) = p(x_{1:t} | z_{1:t}, u_{1:t}, c_{1:t})\prod_{n=1}^N p(m_n | x_{1:t}, z_{1:t}, c_{1:t}) \end{equation} $$ 这个分解的形式说明，路径和地图的后验概率可以拆分为$N+1$个概率分布。

FastSLAM使用粒子滤波器来计算机器人路径的后验概率，标记为$p(x_{1:t} | z_{1:t}, u_{1:t}, c_{1:t})$。对于地图中的每个特征，FastSLAM分别使用一个估计器估计它们的位置$ p(m_n | x_{1:t}, c_{1:t}, z_{1:t}), n = 1, \cdots, N$。因此在FastSLAM中一共有$N+1$个后验概率。特征的估计器以机器人路径作为条件，意味着我们在每个粒子上都有一个特征估计器。对于$M$个粒子，将有$1 + MN$个滤波器。这些概率的乘积形式就是目标后验概率的因式形式。我们在下面会看到，这种因式的形式是一种确切的表示，而不是一种近似。这是SLAM问题的一般特性。

图 13.3. 以贝叶斯网络的形式描述的SLAM问题。机器人通过一系列的控制从位姿$x_{t-1}$运动到$x_{t+2}$。在每个位姿$x_t$上，它都对地图$m = \{m_1, m_2, m_3\}$中附近的特征做出观测。这个图形化的网络说明了位姿变量与地图中的各个特征之间是分离的。如果已知位姿，就不存在其它路径，在地图中的两个特征之间引入未知数值的变量了。这种不需要路径来渲染地图中两个特征的后验概率是条件独立的(给定位姿的情况下)。

为了具体说明这个分解的正确性，图13.3中以动态贝叶斯网络的形式描述了数据处理的过程。如该图所示，每个测量值$z_1, \cdots, z_t$都是对应特征位置的函数，机器人的位姿在测量时就已经确定了。关于机器人路径的知识拆分了各个特征的估计问题，是他们相互之间独立。在图中不存在一条从一个特征到另一个的直接路径，而不会引入机器人路径的变量。因此如果已知机器人路径，那么已知一个状态的确切位置，就不能为我们提供更多的关于其它特征位置的信息。这就一位置式($\ref{f1}$)所提到的，给定机器人路径的情况下特征之间式条件独立的。

在讨论在SLAM问题中应用这一特性之前，让我们先简单的从数学上分析一下。

13.2.1 因式分解的SLAM后验概率的数学推导

暂略。

$$ \begin{equation}\label{f4} p(m_n | x_{1:t}, c_{1:t}, z_{1:t}) = p(m_n | x_{1:t-1}, c_{1:t-1}, z_{1:t-1}) \end{equation} $$ $$ \begin{align}\label{f5} p(m_{c_t} | x_{1:t}, c_{1:t}, z_{1:t}) & = \frac{p(z_t | m_{c_t}, x_{1:t}, c_{1:t}, z_{1:t-1})p(m_{c_t} | x_{1:t}, c_{1:t}, z_{1:t-1})}{p(z_t | x_{1:t}, c_{1:t}, z_{1:t-1}} \\ & = \frac{p(z_t | x_t, m_{c_t}, c_t)p(m_{c_t} | x_{1:t-1}, c_{1:t-1}, z_{1:t-1})}{p(z_t | x_{1:t}, c_{1:t}, z_{1:t-1})} \end{align} $$

13.3 已知数据关联的FastSLAM

后验概率的可因式分解特性，为估计非结构化的后验概率分布的SLAM算法，提供了重要的计算优势。FastSLAM应用因式分解形式，维护了$MN+1$个滤波器， $M$是式($\ref{f1}$)中的因子数量。如此一来，所有的$MN + 1$个滤波器都是低维的。

注意到，FastSLAM使用粒子滤波器估计路径的后验概率，用EKF估计地图特征位置。因为我们的因式分解操作，FastSLAM可以为每个特征维护一个独立的EKF，这使得更新过程比EKF SLAM更高效。每个独立的EKF都是以机器人路径为条件的。因此，每个粒子都有子集的EKF集合。总共有$MN$个EKF滤波器，分别对应着地图中的每个特征和粒子滤波器中的每个粒子。

我们从已知数据关联的情况开始介绍FastSLAM算法。在FastSLAM中粒子被记为: $$ \begin{equation}\label{f11} Y_t^{[k]} = \left\langle x_t^{[k]}, \mu_{1,t}^{[k]}, \Sigma_{1,t}^{[k]}, \cdots, \mu_{N,t}^{[k]}, \Sigma_{N,t}^{[k]} \right\rangle \end{equation} $$ 其中，$[k]$表示粒子的索引，$x_t^{[k]}$是机器人路径估计，$\mu_{n,t}^{[k]}, \Sigma_{n,t}^{[k]}$分别是第$n$个特征关于第$k$个粒子的位置的高斯形式的均值和方差。所有的这些量一起构成了第$k$个粒子$Y_t^{[k]}$，在FastSLAM后验概率中一共有$M$个。

滤波器根据$t-1$时刻的后验概率来估计$t$时刻的后验概率，因此就从$Y_{t-1}$中生成了一个新的粒子集合$Y_t$。新的粒子集合融合了新的控制量$u_t$和具有关联度$c_t$的测量值$z_t$。这个更新过程需要经历如下的阶段:

使用新的位置样本扩展路径后验概率。FastSLAM 1.0使用控制$u_t$为$Y_{t-1}$中的每个粒子采样新的机器人位置$x_t$。更具体的，考虑第$k$个粒子$Y_t^{[k]}$。FastSLAM 1.0根据第$k$个粒子，对位姿$x_t$根据运动后验概率进行采样 $$ \begin{equation}\label{f12} x_t^{[k]} \sim p(x_t | x_{t-1}^{[k]}, u_t) \end{equation} $$ 其中$x_{t-1}^{[k]}$是针对第$k$个粒子，在$t-1$时刻对机器人位姿的后验估计。由此得到的样本$x_t^{[k]}$就会和之前的位姿估计路径$x_{1:t-1}^{[k]}$一起，被添加到一个临时的粒子集合中。这个采样过程如图13.4所示，它列举了从一个初始位姿中采集得到位姿粒子的集合。

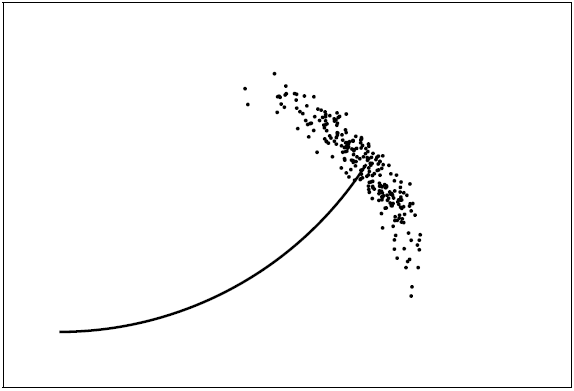
图 13.4.对概率的运动模型的采样。
更新观测到的特征估计。接下来，FastSLAM 1.0更新特征估计的后验概率，表示为期望$\mu_{n,t-1}^{[k]}$和方差$\Sigma_{n,t-1}^{[k]}$。更新的数值接着也会和新的位姿一起被添加到临时的粒子集合中。

确切的更新公式依赖于在$t$时刻是否观测到了特征$m_n$。如果没有观测到特征$n$就记为$n \neq c_t$，我们已经在式($\ref{f4}$)中建立了保持不变的特征的后验概率。这类特征的更新就比较简单 $$ \begin{equation}\label{f13} \left\langle \mu_{n,t}^{[k]}, \Sigma_{n,t}^{[k]} \right\rangle = \left\langle \mu_{n,t-1}^{[k]}, \Sigma_{n,t-1}^{[k]} \right\rangle \end{equation} $$ 对于那些观测到的特征$n = c_t$，就需要通过式($\ref{f5}$)来更新，这里用$\eta$表示归一化算子重写如下 $$ \begin{equation}\label{f14} p(m_{c_t} | x_{1:t}, z_{1:t}, c_{1:t}) = \eta p(z_t | x_t, m_{c_t}, c_t)p(m_{c_t} | x_{1:t-1}, z_{1:t-1}, c_{1:t-1}) \end{equation} $$ 其中概率$p(m_{c_t} | x_{1:t-1}, z_{1:t-1}, c_{1:t-1})$是用期望$\mu_{n,t-1}^{[k]}$和方差$\Sigma_{n,t-1}^{[k]}$表示的$t-1$时刻的高斯函数。 $t$时刻新的状态也是高斯形式的，FastSLAM已和EKF SLAM相同的方式线性化感知模型$p(z_t | x_t, m_{c_t}, c_t)$。和以往一样，我们使用泰勒展开来近似测量函数$h$ $$ \begin{align}\label{f15} h(m_{c_t}, x_t^{[k]}) & \approx h(\mu_{c_t, t-1}^{[k]}, x_t^{[k]}) + h'(x_t^{[k]}, \mu_{c_t, t-1}^{[k]})(m_{c_t} - \mu_{c_t, t-1}^{[k]}) \\ & = \hat{z}_t^{[k]} + H_t^{[k]}(m_{c_t} - \mu_{c_t, t-1}^{[k]}) \\ \hat{z}_t^{[k]} & := h(\mu_{c_t, t-1}^{[k]}, x_t^{[k]}) \\ H_t^{[k]} & := h'(x_t^{[k]}, \mu_{c_t, t-1}^{[k]}) \end{align} $$ 其中，$h'$是$h$关于特征坐标$m_{c_t}$的导数。上式通过$h$在$x_t^{[k]}$和$\mu_{c_t, t-1}^{[k]}$处的正切对$h$做出了线性近似。在这个近似条件下，特征$c_t$的后验概率实际上是一个高斯分布。我们通过标准的EKF测量更新来计算均值和方差: $$ \begin{align}\label{f16} K_t^{[k]} & = \Sigma_{c_t, t-1}^{[k]} H_t^{[k]T} (H_t^{[k]}\Sigma_{c_t, t-1}^{[k]}H_t^{[k]T} + Q_t)^{-1} \\ \mu_{c_t, t}^{[k]} & = \mu_{c_t, t-1}^{[k]} + K_t^{[k]}(z_t - \hat{z}_t^{[k]}) \\ \Sigma_{c_t, t}^{[k]} & = (I - K_t^{[k]} H_t^{[k]})\Sigma_{c_t, t-1}^{[k]} \end{align} $$ 重复步骤1和步骤2 $M$次，就可以得到一个$M$个粒子的临时集合。

重采样。这是最后一个步骤，FastSLAM对临时粒子集进行重采样。我们已经在很多算法中讨论过了重采样技术。FastSLAM根据重要性权重对粒子集合进行重采样，有些粒子将被移除，也会新增一些粒子。如此得到了$M$个粒子就构成了新的最终粒子集合$Y_t$。之所以有必要进行重采样，是因为临时集合中的粒子描述的不是目标后验概率。在步骤1中只是根据最近的控制量$u_t$生成了位姿$x_t$，没有关注过测量值$z_t$。读者现在应该比较清楚，重采样是粒子滤波器中矫正这一偏差的常用技术。

我们在图13.5中再次以一个一维地粒子来示例这一过程。图中虚线表示建议分布proposal distribution，它是生成粒子地分布，实线则是目标分布。在FastSLAM中，建议分布不依赖于$z_t$，但是目标分布依赖。图中低下是加权地粒子，根据它们的这些权重，所得到的粒子集合实际上是对目标权重的一种近似。

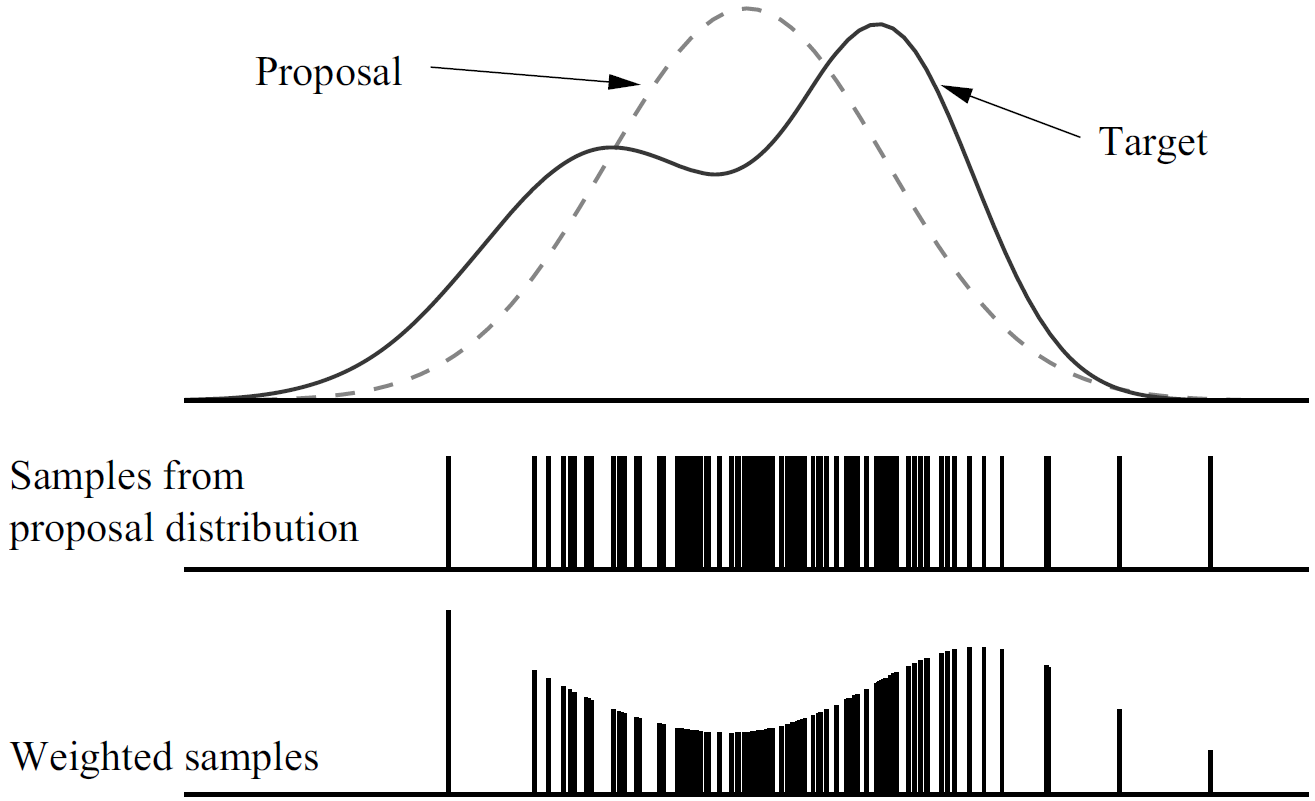
图 13.5.我们不能方便地对目标分布采样。实际上，重要性采样器从建议分布上采样，如图中虚线所示，它具有更简单地形式。下面是从建议分布中采集地样本，条码地长度正比于它们的重要性权重。

为了确定重要性因子，事实证明在计算临时集合中路径粒子的实际建议分布是很有用的。假设路径粒子集合$Y_{t-1}$服从$p(x_{1:t-1} | z_{1:t-1}, u_{1:t-1}, c_{1:t-1})$的分布，这是一种渐进正确的近似，临时路径粒子集合服从分布: $$ \begin{equation}\label{f19} p(x_{1:t}^{[k]} | z_{1:t-1}, u_{1:t}, c_{1:t-1}) = p(x_t^{[k]} | x_{t-1}^{[k]}, u_t)p(x_{1:t-1}^{[k]} | z_{1:t-1}, u_{1:t-1}, c_{1:t-1}) \end{equation} $$ 因子$p(x_t^{[k]} | x_{t-1}^{[k]}, u_t)$是式($\ref{f12}$)中的样本分布。

目标分布考虑了当前测量值$z_t$及其对应的关联$c_t$: $$ \begin{equation}\label{f20} p(x_{1:t}^{[k]} | z_{1:t}, u_{1:t}, c_{1:t}) \end{equation} $$ 重采样过程考虑了目标分布于建议分布之间的差异。采样的重要性因子importance factor由目标分布和建议分布的商给出: $$ \begin{align}\label{f21} w_t^{[k]} & = \frac{\mathrm{target\ distribution}}{\mathrm{proposal\ distribution}} \\ & = \frac{p(x_{1:t}^{[k]} | z_{1:t}, u_{1:t}, c_{1:t})}{p(x_{1:t}^{[k]} | z_{1:t-1}, u_{1:t}, c_{1:t-1})} \\ & = \eta p(z_t | x_t^{[k]}, c_t) \end{align} $$ 上式中最后一次的变换由如下形式得出 $$ \begin{align}\label{f22} p(x_{1:t}^{[k]} | z_{1:t}, u_{1:t}, c_{1:t}) & = \eta p(z_t | x_{1:t}^{[k]}, z_{1:t-1}, u_{1:t}, c_{1:t})p(x_{1:t}^{[k]} | z_{1:t-1}, u_{1:t}, c_{1:t}) \\ & = \eta p(z_t | x_t^{[k]}, c_t)p(x_{1:t}^{[k]} | z_{1:t-1}, u_{1:t}, c_{1:t-1}) \end{align} $$ 为了计算式($\ref{f21}$)中的概率$p(z_t | x_t^{[k]}, c_t)$，有必要对其进一步变换一下。具体的，这个概率于如下的积分等价，这里我们再次省略了与预测传感器测量值无关的变量: $$ \begin{align}\label{f23} w_t^{[k]} & = \eta \int p(z_t | m_{c_t}, x_t^{[k]}, c_t)p(m_{c_t} | x_t^{[k]}, c_t)dm_{c_t} \\ & = \eta \int p(z_t | m_{c_t}, x_t^{[k]}, c_t)p(m_{c_t} | x_{1:t-1}^{[k]}, z_{1:t-1} c_{1:t-1})dm_{c_t} \\ p(m_{c_t} | x_{1:t-1}^{[k]}, z_{1:t-1} c_{1:t-1}) & \sim \mathcal{N}(\mu_{c_t, t-1}^{[k]}, \Sigma_{c_t, t-1}^{[k]}) \end{align} $$ 其中$\mathcal{N}(x; \mu, \Sigma)$表示变量$x$服从均值位$\mu$方差$\Sigma$的高斯分布。

式($\ref{f23}$)涉及到估计$t$时刻观测到的特征位置以及测量模型。为了以闭合形式计算式($\ref{f23}$)，FastSLAM使用在步骤2中更新测量值时相同的线性近似。特别的，重要性因子可以通过如下形式得出: $$ \begin{equation}\label{f24} w_t^{[k]} \sim \eta \left|2\pi Q_t^{[k]}\right|^{-\frac{1}{2}} \exp \left\{ -\frac{1}{2}(z_t - \hat{z}_t^{[k]})Q_t^{[k]-1}(z_t -\hat{z}_t^{[k]}) \right\} \end{equation} $$ 其中协方差为 $$ \begin{equation}\label{f25} Q_t^{[k]} = H_t^{[k]T} \Sigma_{n,t-1}^{[k]} H_t^{[k]} + Q_t \end{equation} $$ 这个表达式时实际的测量值$z_t$在高斯分布下的概率。通过使用$h$的线性化近似，对式($\ref{f23}$)卷积就得到了这个结果。得到的重要性权重用于从临时样本集合中采样$M$个新的样本。通过这个重采样过程，粒子存活下来的概率正比于它们的测量概率。

这三个步骤一起构成了应用于已知数据关联度的SLAM问题的FastSLAM 1.0算法的更新规则。我们注意到更新的运行时间并不依赖于整个路径长度$t$。实际上，只有最近一次的位姿$x_{t-1}^{[k]}$被用于生成$t$时刻的新粒子。因此，我们可以安全的扔掉过去的位姿。这个结果都是令人兴奋的，FastSLAM在获取数据的时候，无论是在时间上，还是空间上，都不依赖于时间步的总数。

算法13.1中总结了已知数据关联的FastSLAM 1.0算法。为了简化，这一实现假设在一个时间点上只观测到了一个特征。这个算法以一种直接的方法实现了各个更新过程。尽管其实线比较简单直接，实际上FastSLAM 1.0式最早实现的SLAM算法之一。

算法 13.1.已知关联的FastSLAM 1.0。

13.4 改进建议分布

FastSLAM 2.0大致上等价于FastSLAM 1.0，它有一个重要的扩展，在对位姿$x_t$采样的时候考虑了测量值$z_t$。这样做可以克服FastSLAM 1.0的关键限制。

表面上，差异很小，读者可能记得FastSLAM 1.0只基于控制量$u_t$对位姿采样，然后使用测量值$z_t$计算重要性权重。当控制量的精度低于机器人传感器的精度时，这就会产生问题。图13.6中就示例了这一情况。其中图13.6a中显示了生成大量样本的建议分布，但是只有一小部分的子集具有较高的似然度，如图中椭圆所示。在重采样之后，只有椭圆中的样本因为它们相对较高的似然度而存活了下来。FastSLAM 2.0通过基于测量值$z_t$和控制量$u_t$的位姿采样避免了这一问题。因此，FastSLAM 2.0比FastSLAM 1.0更高效。另一方面，FastSLAM 2.0实现起来要比FastSLAM 1.0困难一些，而且它的数学推导过程也更复杂。

图 13.6.推荐分布和后验分布之间的差异。(a)。FastSLAM 1.0生成成的样本和根据测量值(椭圆)生成的后验概率。 (b) 重采样后的样本集合。

13.4.1 通过对新位姿采样扩展路径后验概率

在FastSLAM 2.0中，从后验概率中采样获得位姿$x_t^{[k]}$ $$ \begin{equation}\label{f26} x_t^{[k]} \sim p(x_t | x_{1:t-1}^{[k]}, u_{1:t}, z_{1:t}, c_{1:t}) \end{equation} $$ 这一分布与式($\ref{f12}$)不同，在式($\ref{f26}$)中考虑了测量值$z_t$及其关联$c_t$。具体的，式($\ref{f26}$)以$z_{1:t}$作为条件，而FastSLAM 1.0中的位姿采样器则是以$z_{1:t-1}$为条件的。

不幸的是，它在数学形式上更复杂。我们需要进一步分析式($\ref{f26}$)的采样机制。首先我们将式($\ref{f26}$)用测量模型和运动模型等已知的分布展开，那么第$k$个样本的高斯特征估计为 $$ \begin{align}\label{f27} p(x_t | x_{1:t-1}^{[k]}, u_{1:t}, z_{1:t}, c_{1:t}) & = \frac{p(z_t | x_t, x_{1:t-1}^{[k]}, u_{1:t}, z_{1:t-1}, c_{1:t}) p(x_t | x_{1:t-1}^{[k]}, u_{1:t}, z_{1:t-1}, c_{1:t})}{p(z_t | x_{1:t-1}^{[k]}, u_{1:t}, z_{1:t-1}, c_{1:t})} \\ & = \eta^{[k]} p(z_t | x_t, x_{1:t-1}^{[k]}, u_{1:t}, z_{1:t-1}, c_{1:t}) p(x_t | x_{1:t-1}^{[k]}, u_{1:t}, z_{1:t-1}, c_{1:t}) \\ & = \eta^{[k]} p(z_t | x_t, x_{1:t-1}^{[k]}, u_{1:t}, z_{1:t-1}, c_{1:t}) p(x_t | x_{t-1}^{[k]}, u_t) \\ & = \eta^{[k]} p(x_t | x_{t-1}^{[k]}, u_t) \int p(z_t | m_{c_t} x_t, x_{1:t-1}^{[k]}, u_{1:t}, z_{1:t-1}, c_{1:t}) p(m_{c_t} | x_t, x_{1:t-1}^{[k]}, u_{1:t}, z_{1:t-1}, c_{1:t}) dm_{c_t} \\ & = \eta^{[k]} p(x_t | x_{t-1}^{[k]}, u_t)\int p(z_t | m_{c_t}, x_t, c_t) p(m_{c_t} | x_{1:t-1}^{[k]}, z_{1:t-1}, c_{1:t-1}) dm_{c_t} \\ p(x_t | x_{t-1}^{[k]}, u_t) & \sim \mathcal{N}(x_t; g(x_{t-1}^{[k]}, u_t), R_t) \\ p(z_t | m_{c_t}, x_t, c_t) & \sim \mathcal{N}(z_t; h(m_{c_t}, x_t), Q_t) \\ p(m_{c_t} | x_{1:t-1}^{[k]}, z_{1:t-1}, c_{1:t-1}) & \sim \mathcal{N}(m_{c_t}; \mu_{c_t,t-1}^{[k]}, \Sigma_{c_t, t-1}^{[k]}) \end{align} $$ 通过这个表达式可以清楚的看到我们的样本分布实际上式两个高斯分布卷积与第三个分布的乘积。在一般的SLAM问题中，样本分布不具有容易采样的封闭形式。其罪魁祸首就是函数$h$，如果它是线性的，那么这个概率就是高斯分布，这一点将在后面的内容中介绍。实际上，式($\ref{f27}$)中的积分不具有封闭形式的解。因此对其采样是一件困难的任务。

这一现象促使我们使用一个线性近似来替代$h$。与本书中大多数情况一样，这一近似是通过一阶泰勒展开获得的，有如下形式的线性函数: $$ \begin{equation}\label{f28} h(m_{c_t}, x_t) \approx \hat{z}_t^{[k]} + H_m(m_{c_t} - \mu_{c_t, t-1}^{[k]}) + H_x(x_t - \hat{x}_t^{[k]}) \end{equation} $$ 这里我们使用如下的标记: $$ \begin{equation}\label{f29} \hat{z}_t^{[k]} = h(\mu_{c_t,t-1}^{[k]}, \hat{x}_t^{[k]} \end{equation} $$ $$ \begin{equation}\label{f30} \hat{x}_t^{[k]} = g(x_{c_t,t-1}^{[k]}, u_t) \end{equation} $$ 矩阵$H_m$和$H_x$是$h$的雅可比矩阵。它们分别是$h$关于$m_{c_t}$和$x_t$的微分，在参数期望值处的取值: $$ \begin{equation}\label{f31} H_m = \nabla_{m_{c_t}} h(m_{c_t}, x_t) \mid_{ x_t = \hat{x}_t^{[k]}; m_{c_t} = \mu_{c_t, t-1}^{[k]}} \end{equation} $$ $$ \begin{equation}\label{f32} H_x = \nabla_{x_{c_t}} h(m_{c_t}, x_t) \mid_{ x_t = \hat{x}_t^{[k]}; m_{c_t} = \mu_{c_t, t-1}^{[k]}} \end{equation} $$ 在这个近似情况下，目标样本分布($\ref{f27}$)就是一个具有如下参数的高斯分布 $$ \begin{equation}\label{f33} \Sigma_{x_t}^{[k]} = \left[ H_x^T Q_t^{[k]-1} H_x + R_t^{-1} \right]^{-1} \end{equation} $$ $$ \begin{equation}\label{f34} \mu_{x_t}^{[k]} = \Sigma_{x_t}^{[k]}H_x^T Q_t^{[k]-1} (z_t - \hat{z}_t^{[k]}) + \hat{x}_t^{[k]} \end{equation} $$ 其中矩阵$Q_t^{[k]}$定义如下 $$ \begin{equation}\label{f35} Q_t^{[k]} = Q_t + H_m\Sigma_{c_t, t-1}^{[k]}H_m^T \end{equation} $$ 我们注意到在线性近似背后的卷积理论为我们提供了式($\ref{f27}$)中积分项的封闭形式 $$ \begin{equation}\label{f36} \mathcal{N}(z_t; \hat{z}_t^{[k]} + H_x x_t - H_x\hat{x}_t^{[k]}, Q_t^{[k]}) \end{equation} $$ 现在，样本分布($\ref{f27}$)就是由正态分布的积构成，其中与积分相乘的一项服从正态分布$\mathcal{N}(x_t; \hat{x}_t^{[k]}, R_t)$。写成高斯形式，我们有 $$ \begin{equation}\label{f37} p(x_t | x_{1:t-1}^{[k]}, u_{1:t}, z_{1:t}, c_{1:t}) = \eta \exp \left\{ -P_t^{[k]} \right\} \end{equation} $$ 其中 $$ \begin{equation}\label{f38} p_t^{[k]} = \frac{1}{2}\left[(z_t - \hat{z}_t^{[k]} - H_x x_t + H_x \hat{x}_t^{[k]})^T Q_t^{[k]-1} (z_t - \hat{z}_t^{[k]} - H_x x_t + H_x \hat{x}_t^{[k]}) + (x_t - \hat{x}_t^{[k]})^T R_t^{-1} (x_t - \hat{x}_t^{[k]}) \right] \end{equation} $$ 该式显然是我们的目标变量$x_t$的二次型，因此$p(x_t | x_{1:t-1}^{[k]}, u_{1:t}, z_{1:t}, c_{1:t})$是高斯分布。其均值和方差等价于$P_t^{[k]}$的最小值和其曲率。它们可以通过对$P_t^{[k]}$关于$x_t$求一阶和二阶偏导计算得到 $$ \begin{align}\label{f39} \frac{\partial P_t^{[k]}}{\partial x_t} & = -H_x^T Q_t^{[k]-1} (z_t - \hat{z}_t^{[k]} - H_x x_t + H_x \hat{x}_t^{[k]}) + R_t^{-1}(x_t - \hat{x}_t^{[k]}) \\ & = (H_x^T Q_t^{[k]-1} H_x + R_t^{-1})x_t - H_x^T Q_t^{[k]-1} (z_t - \hat{z}_t^{[k]} + H_x \hat{x}_t^{[k]} - R_t^{-1}\hat{x}_t^{[k]}) - R_t^{-1}\hat{x}_t^{[k]} \\ \frac{\partial^2 P_t^{[k]}}{\partial x_t^2} & = H_x^T Q_t^{[k]-1} H_x + R_t^{-1} \end{align} $$ 样本分布的协方差$\Sigma_{x_t}^{[k]}$就可以通过对二阶导数求逆得到 $$ \begin{equation}\label{f41} \Sigma_{x_t}^{[k]} = \left[ H_x^T Q_t^{[k]-1} H_x + R_t^{-1} \right]^{-1} \end{equation} $$ 同一分布的均值$\mu_{x_t}^{[k]}$可以通过令式($\ref{f39}$)中的一阶导数为0求得。 $$ \begin{align}\label{f42} \mu_{x_t}^{[k]} & = \Sigma_{x_t}^{[k]} \left[ H_x^T Q_t^{[k]-1} (z_t - \hat{z}_t^{[k]} + H_x \hat{x}_t^{[k]}) + R_t^{-1}\hat{x}_t^{[k]} \right] \\ & = \Sigma_{x_t}^{[k]} H_x^T Q_t^{[k]-1} (z_t - \hat{z}_t^{[k]}) + \Sigma_{x_t}^{[k]}\left[ H_x^T Q_t^{[k]-1} H_x + R_t^{-1} \right] \hat{x}_t^{[k]} \\ & = \Sigma_{x_t}^{[k]} H_x^T Q_t^{[k]-1} (z_t - \hat{z}_t^{[k]}) + \hat{x}_t^{[k]} \end{align} $$ 这个高斯分布就是FastSLAM 2.0中对目标样本分布($\ref{f26}$)的近似。显然，这个建议分布比FastSLAM 1.0中的采样器中所用的要复杂一些。

13.4.2 更新观测的特征估计

就像我们的FastSLAM算法的第一个版本一样，FastSLAM 2.0基于测量值$z_t$和采样的位姿$x_t^{[k]}$估计特征并更新后验概率。在$t-1$时刻的估计通过均值$\mu_{j,t-1}^{[k]}$和方差$\Sigma_{j,t-1}^{[k]}$表示。更新的估计就是$\mu_{j,t}^{[k]}$和$\Sigma_{j,t}^{[k]}$。更新的本质依赖于在$t$时刻是否观测到特征$j$。对于$j \neq c_t$，我们已经在式($\ref{f4}$)中建立了为保持不变的特征的后验估计。这意味我们不用更新它们的估计，只需要拷贝它们就可以了。

对于观测到的特征$j = c_t$，这种情况更复杂一些。式($\ref{f5}$)中已经描述了观测到特征的后验概率。这里我们在粒子$k$的情形下重写如下 $$ \begin{align}\label{f43} p(m_{c_t} | x_t^{[k]}, c_{1:t}, z_{1:t}) & = \eta p(z_t | m_{c_t}, x_t^{[k]}, c_t) p(m_{c_t} | x_{1:t-1}^{[k]}, z_{1:t-1}, c_{1:t-1}) \\ p(z_t | m_{c_t}, x_t^{[k]}, c_t) & \sim \mathcal{N}(z_t; h(m_{c_t}, x_t^{[k]}), Q_t) \\ p(m_{c_t} | x_{1:t-1}^{[k]}, z_{1:t-1}, c_{1:t-1}) & \sim \mathcal{N}(m_{c_t}; \mu_{c_t, t-1}^{[k]}, \Sigma_{c_t, t-1}^{[k]}) \end{align} $$ 根据式($\ref{f27}$)，$h$的非线性度导致该后验概率不是高斯分布，这与FastSLAM 2.0中使用高斯分布表示特征估计的理念相悖。幸运的是，我们完全可以用相同的线性化方法来近似: $$ \begin{equation}\label{f44} h(m_{c_t}, x_t) \sim \hat{z}_t^{[k]} + H_m(m_{c_t} - \mu_{c_t, t-1}^{[k]}) \end{equation} $$ 注意到这里的$x_t$并不是一个自由变量，因此我们可以省略到式($\ref{f28}$)中的第三项。这个近似将概率($\ref{f43}$)表示成为目标变量$m_{c_t}$的高斯分布 $$ \begin{equation}\label{f45} p(m_{c_t} | x_t^{[k]}, c_{1:t}, z_{1:t}) = \eta \exp \left\{ -\frac{1}{2} \left(z_t - \hat{z}_t^{[k]} - H_m\left(m_{c_t} - \mu_{c_t, t-1}^{[k]}\right)\right) Q_t^{-1} \left(z_t - \hat{z}_t^{[k]} - H_m\left(m_{c_t} - \mu_{c_t, t-1}^{[k]}\right)\right) -\frac{1}{2} \left(m_{c_t} - \mu_{c_t, t-1}^{[k]}\right) \Sigma_{c_t, t-1}^{[k]-1} \left(m_{c_t} - \mu_{c_t, t-1}^{[k]}\right) \right\} \end{equation} $$ 新的均值和方差可以通过标准EKF测量更新公式得到: $$ \begin{align}\label{f46} K_t^{[k]} & = \Sigma_{c_t, t-1}^{[k]} H_m^T Q_t^{[k]-1} \\ \mu_{c_t,t}^{[k]} & = \mu_{c_t, t-1}^{[k]} K_t^{[k]}\left(z_t - \hat{z}_t^{[k]}\right) \\ \Sigma_{c_t,t}^{[k]} & = \left(I - K_t^{[k]} H_m\right)\Sigma_{c_t,t-1}^{[k]} \\ \end{align} $$ 我们注意到，这比FastSLAM 1.0的更新过程要复杂一点，但是它提高了准确度，为之在实现的时候多付出一些努力也是值得的。

13.4.3 计算重要性因子

目前所生成的粒子还没有与目标后验概率匹配上。在FastSLAM 2.0中，这都要归咎于式($\ref{f27}$)中的归一化因子$\eta^{[k]}$，它通常在每个粒子$k$上都不一样。这一不同并没有在重采样过程中得到考虑。在FastSLAM 1.0中，重要性因子式通过如下的商给出的: $$ \begin{equation}\label{f49} w_t^{[k]} = \frac{\mathrm{target distribution}}{\mathrm{proposal distribution}} \end{equation} $$ 我们希望粒子所描述的路径后验概率$p(x_t^{[k]} | z_{1:t}, u_{1:t}, c_{1:t})$就是对目标分布的描述。在渐进修正的假设下，我们根据上一个时间点的目标分布$p(x_{1:t-1}^{[k]} | z_{1:t-1}, u_{1:t-1}, c_{1:t-1}$，生成$x_{1:t-1}^{[k]}$所描述的路径。我们之一到这个建议分布现在可以表示成积: $$ \begin{equation}\label{f50} p(x_{1:t-1}^{[k]} | z_{1:t-1}, u_{1:t-1}, c_{1:t-1}) p(x_t^{[k]} | x_{1:t-1}^{[k]}, u_{1:t},, z_{1:t}, c_{1:t}) \end{equation} $$ 上式积中的第二项式位姿样本分布($\ref{f27}$)。其重要性权重可以根据下式计算得到: $$ \begin{align}\label{f51} w_t^{[k]} & = \frac{p\left(x_t^{[k]} | u_{1:t}, z_{1:t}, c_{1:t})\right)} {p\left(x_t^{[k]} | x_{1:t-1}^{[k]}, u_{1:t}, z_{1:t}, c_{1:t}\right)p\left(x_{1:t-1}^{[k]} | u_{1:t-1}, z_{1:t-1}, c_{1:t-1} \right)} \\ & = \frac{p\left(x_t^{[k]} | x_{1:t-1}^{[k]}, u_{1:t}, z_{1:t}, c_{1:t}\right)p\left(x_{1:t-1}^{[k]} | u_{1:t}, z_{1:t}, c_{1:t}\right)} {p\left(x_t^{[k]} | x_{1:t-1}^{[k]}, u_{1:t}, z_{1:t}, c_{1:t}\right)p\left((x_{1:t-1}^{[k]} | u_{1:t-1}, z_{1:t-1}, c_{1:t-1}\right)} \\ & = \frac{p\left(x_{1:t-1}^{[k]} | u_{1:t}, z_{1:t}, c_{1:t}\right)}{p\left(x_{1:t-1}^{[k]} | u_{1:t-1}, z_{1:t-1}, c_{1:t-1}\right)} \\ & = \eta \frac{p\left(z_t | x_{1:t-1}^{[k]}, u_{1:t}, z_{1:t-1}, c_{1:t}\right)p\left(x_{1:t-1}^{[k]} | u_{1:t}, z_{1:t-1}, c_{1:t}\right)} {p\left(x_{1:t-1}^{[k]} | u_{1:t-1}, z_{1:t-1}, c_{1:t-1}\right)} \\ & = \eta \frac{p\left(z_t | x_{1:t-1}^{[k]}, u_{1:t}, z_{1:t-1}, c_{1:t}\right)p\left(x_{1:t-1}^{[k]} | u_{1:t-1}, z_{1:t-1}, c_{1:t-1}\right)} {p\left(x_{1:t-1}^{[k]} | u_{1:t-1}, z_{1:t-1}, c_{1:t-1}\right)} \\ & = \eta p(z_t | x_{1:t-1}^{[k]}, u_{1:t}, z_{1:t-1}, c_{1:t}) \end{align} $$ 读者可能注意到这个表达式时式($\ref{f27}$)中的归一化因子$\eta^{[k]}$的逆。更进一步的变换，我们有如下的形式: $$ \begin{align}\label{f52} w_t^{[k]} & = \eta \int p\left(z_t | x_t, x_{1:t-1}^{[k]}, u_{1:t}, z_{1:t-1}, c_{1:t}\right) p\left(x_t | x_{1:t-1}^{[k]}, u_{1:t}, z_{1:t-1}, c_{1:t}\right) dx_t \\ & = \eta \int p\left(z_t | x_t, x_{1:t-1}^{[k]}, u_{1:t}, z_{1:t-1}, c_{1:t}\right) p\left(x_t | x_{t-1}^{[k]}, u_t\right)dx_t \\ & = \eta \int \int p\left(z_t | m_{c_t}, x_t, x_{1:t-1}^{[k]}, u_{1:t}, z_{1:t-1}, c_{1:t}\right) p\left(m_{c_t} | x_t, x_{1:t-1}^{[k]}, u_{1:t}, z_{1:t-1}, c_{1:t}\right)dm_{c_t} p(x_t | x_{t-1}^{[k]}, u_t) dx_t \\ & = \eta \int p\left(x_t | x_{t-1}^{[k]}, u_t\right) \int p\left(z_t | m_{c_t}, x_t, c_t\right) p\left(m_{c_t} | x_{1:t-1}^{[k]}, u_{1:t-1}, z_{1:t-1}, c_{1:t-1}\right) dm_{c_t} dx_t \\ p\left(x_t | x_{t-1}^{[k]}, u_t\right) & \sim \mathcal{N}(x_t; g(\hat{x}_{t-1}^{[k]}, u_t) R_t) \\ p\left(z_t | m_{c_t}, x_t, c_t\right) & \sim \mathcal{N}(z_t; h(m_{c_t}, x_t), Q_t) \\ p\left(m_{c_t} | x_{1:t-1}^{[k]}, u_{1:t-1}, z_{1:t-1}, c_{1:t-1}\right) & \sim \mathcal{N}(m_{c_t}; \mu_{c_t, t-1}^{[k]}, \Sigma_{c_t, t-1}^{[k]}) \end{align} $$ 我们发现这个表达式也可以通过对$h$线性化，用关于测量值$z_t$的高斯分布来近似。如之前看到的那样，所得到的高斯分布的均值为$\hat{z}_t$，其方差为 $$ \begin{equation}\label{f53} L_t^{[t]} = H_x^T Q_t H_x + H_m \Sigma_{c_t, t-1}^{[k]} H_m^T + R_t \end{equation} $$ 换句话说，第$k$个粒子的重要性因子可以由如下的表达式给出: $$ \begin{equation}\label{f54} w_t^{[k]} = \left| 2\pi L_t^{[t]} \right|^{-\frac{1}{2}} \exp \left\{ -\frac{1}{2}(z_t - \hat{z}_t)L_t^{[t]-1}(z_t - \hat{z}_t) \right\} \end{equation} $$ 和FastSLAM 1.0一样，在步骤1和2中生成粒子，在步骤3中为它们赋予一个重要性因子，这些粒子一起构成了一个临时的粒子集合。

FastSLAM 2.0中的最后一个更新过程就是重采样。和FastSLAM 1.0一样，FastSLAM 2.0从临时粒子集合中采样$M$个粒子。每个粒子的采样概率正比于其重要性因子$w_t^{[k]}$。如此得到的粒子集合就渐进的表示$t$时刻的目标后验概率。

13.5 未知数据关联

本部分将两种FastSLAM算法扩展到关联度变量$c_{1:t}$未知的情况下。使用粒子滤波器进行SLAM的关键优势就是每个粒子都有它自己的局部数据关联决策。

我们提醒读者，所谓的数据关联问题就是根据可用的数据确定$t$时刻变量$c_t$的取值的问题。这一问题如图13.7所示，图中机器人观测到了世界中额两个特征。根据相对于这些特征的实际位姿，测量对应着地图中的不同特征，如图中的星星所示。

图 13.7.SLAM中的数据关联问题。本图想要说明最好的数据关联可能因为机器人位姿的不同而有变化。

到目前为止，我们已经讨论了很多数据关联技术，比如说最大似然估计。这些技术有一个共同点就是对于整个滤波器，在一次测量的时候只有一个数据关联。 FastSLAM由于使用了多个粒子，所以可以基于每个粒子确定数据关联。因此，滤波器不仅仅对机器人路径采样，而且对沿途可能的数据关联做出决策。

这是FastSLAM算法的关键特性，不同于很多高斯SLAM算法。只要有一小部分的粒子做出了正确的数据关联，就不会产生EKF算法那样致命的数据关联错误。错误的数据关联将使得粒子具有非一致的地图，这将增大其在未来的重采样过程中被移除粒子集的概率。

每个粒子的数据关联的数学定义很直接，它将每个滤波器的数据关联扩展到了独立的粒子上。每个粒子维护了一个局部的数据关联变量集合，记为$\hat{c}_t^{[k]}$。在极大似然数据关联中，每个$\hat{c}_t^{[k]}$通过最大化测量值$z_t$的似然值来确定 $$ \begin{equation}\label{f55} \hat{c}_t^{[k]} = \arg \max_{c_t} p\left(z_t | c_t, \hat{c}_{1:t-1}^{[k]}, x_{1:t}^{[k]}, z_{1:t-1}, u_{1:t} \right) \end{equation} $$ 我们还可以使用数据关联采样器Data Association Sampler, DAS，根据它们的似然度采样数据关联变量 $$ \begin{equation}\label{f56} \hat{c}_t \sim \eta p\left(z_t | c_t, \hat{c}_{1:t-1}, x_{1:t}^{[k]}, z_{1:t-1}, u_{1:t} \right) \end{equation} $$ ML和DAS这两种技术，都可以估计地图中特征的数量。使用ML的SLAM技术，当地图中所有已知特征的似然度低于一个阈值$p_0$，就会创建新的特征。DAC将一个观测到的测量值，随机的与一个新的之前为观测到的特征联系起来。它们通过正比于$\eta p_0$的概率来实现这一点，其中$\eta$是定义在式($\ref{f56}$)中的归一化算子。 $$ \begin{equation}\label{f57} \hat{c}_t^{[k]} \sim \eta p(z_t | c_t, \hat{c}_{1:t-1}^{[k]}, x_{1:t}^{[k]}, z_{1:t-1}, u_{1:t}) \end{equation} $$ 对于这两种技术，似然度都可以通过下式计算: $$ \begin{align}\label{f58} p\left(z_t | c_t, \hat{c}_{1:t-1}^{[k]}, x_{1:t}^{[k]}, z_{1:t-1}, u_{1:t}\right) & = \int p\left(z_t | m_{c_t}, c_t, \hat{c}_{1:t-1}^{[k]},x_{1:t}^{[k]}, z_{1:t-1}, u_{1:t}\right) p\left(m_{c_t} | c_t, \hat{c}_{1:t-1}^{[k]}, x_{1:t}^{[k]}, z_{1:t-1}, u_{1:t}\right)dm_{c_t} \\ & = \int p\left(z_t | m_{c_t}, c_t, x_t^{[k]}\right) p\left(m_{c_t} | \hat{c}_{1:t-1}^{[k]}, x_{1:t-1}^{[k]}, z_{1:t-1} \right) dm_{c_t} \\ p\left(z_t | m_{c_t}, c_t, x_t^{[k]}\right) & \sim \mathcal{N}\left(z_t; h\left(m_{c_t}, x_t^{[k]}\right), Q_t\right) \\ p\left(m_{c_t} | \hat{c}_{1:t-1}^{[k]}, x_{1:t-1}^{[k]}, z_{1:t-1} \right) & \sim \mathcal{N}\left(\mu_{c_t,t-1}^{[k]}, \Sigma_{c_t,t-1}^{[k]}\right) \end{align} $$ $h$的线性化使得我们得到了如下的封闭形式: $$ \begin{equation}\label{f59} p\left(z_t | c_t, \hat{c}_{1:t-1}^{[k]}, x_t^{[k]}, z_{1:t-1}, u_{1:t}\right) = \left| 2 \pi Q_t^{[k]} \right|^{-\frac{1}{2}} \exp \left\{ -\frac{1}{2}\left(z_t - h\left(\mu_{c_t, t-1}^{[k]}, x_t^{[k]}\right) \right)^T Q_t^{[k]-1} \left(z_t - h\left(\mu_{c_t, t-1}^{[k]}, x_t^{[k]}\right) \right) \right\} \end{equation} $$ 变量$Q_t^{[k]}$在式($\ref{f35}$)中定义，式数据关联变量$c_t$的一个函数。新添加到地图中的特征完全与上述的形式一样。在ML算法中，当概率$p(z_t | c_t, \hat{c}_{1:t-1}^{[k]}, x_t^{[k]}, z_{1:t-1}, u_{1:t})$低于了一个阈值$p_0$时，就会添加一个特征。DAS引入了一个假设，当观测到一个之前为观测到的特征时，就以概率$\eta p_0$采样(The DAS includes the hypothesis that an observation corresponds to a previously unobserved feature in its set of hypotheses, and samples it with probability $\eta p_0$)。

13.6 地图管理

在FastSLAM中地图管理很大程度上与EKF SLAM一样，只是一些粒子由FastSLAM中解决数据关联问题时产生的。

在其它SLAM算法中，任何新添加的特征都需要初始化一个卡尔曼滤波器。在很多SLAM问题中，测量函数$h$是可逆的invertible。这就是说，机器人在平面内的距离和方向角的测量，单一的测量就足以产生对特征位置的估计。EKF的初始化就比较直接了: $$ \begin{align}\label{f60} x_t^{[k]} & \sim p\left( x_t | x_{t-1}^{[k]}, u_t\right) \\ \mu_{n,t}^{[k]} & = h^{-1}\left(z_t, x_t^{[k]}\right) \\ \Sigma_{n,t}^{[k]} & = \left(H_{\hat{c}}^{[k]T}Q_t^{-1}H_{\hat{c}}^{[k]} \right)^{-1}\ \ \mathrm{with}\ \ H_{\hat{c}}^{[k]} = h'\left(\mu_{n,t}^{[k]}, x_t^{[k]}\right) \\ w_t^{[k]} & = p_0 \end{align} $$ 注意那些新观测到的特征，位姿$x_t^{[k]}$是根据运动模型$p\left(x_t | x_{t-1}^{[k]}, u_t\right)$采样的。当之前的位置估计都不能用于观测到的特征时，这一分布与FastSLAM采样分布($\ref{f36}$)等价。

Deans and Hebert (2002)讨论了$h$不是可逆的情况。一般来说，这一情形需要对多个测量值累加，来获得线性化$h$的一个较好的估计。

为了解决错误的将特征引入地图的问题，FastSLAM的特征机制可以消除那些没有足够证据支撑的特征。就像EKF SLAM那样，FastSLAM通过跟踪地图中各个特征实际存在的对数odds来实现这一点。

具体的，当观测到一个特征的时候，就增加其对数odds一个固定的值，该值通过标准的贝叶斯滤波器计算得到。类似的，当本应该观测到一个特征却没有观测到它的时候，这种反面信息将导致特征存在值以一个固定的数量降低。对于那些存在变量低于一个阈值的特征，我们就简单的将他们从粒子列表中移除。我们也可以在FastSLAM中实现一个临时的特征列表。这个技术实现起来很琐碎，因为每个特征都有自己的粒子。

13.7 FastSLAM算法

算法13.2和算法13.3中总结了两种未知数据关联的FastSLAM算法。在这两个算法中，粒子具有如下的形式 $$ \begin{equation}\label{f64} Y_t^{[k]} = \left\langle x_t^{[k]}, N_t^{[k]}, \left\langle \mu_{1,t}^{[k]}, \Sigma_{1,t}^{[k]}, \tau_1^{[k]} \right\rangle, \cdots, \left\langle \mu_{N_t^{[k]},t}^{[k]}, \Sigma_{N_t^{[k]},t}^{[k]}, \tau_{N_t^{[k]}}^{[k]} \right\rangle \right\rangle \end{equation} $$ 除了位姿$x_t^{[k]}$和特征估计$\mu_{n,t}^{[k]}$和$\Sigma_{n,t}^{[k]}$，每个粒子都在其局部地图中维护了数量$N_t^{[k]}$的特征，并且每个特征都携带着一个估计其存在的概率$\tau_n^{[k]}$。滤波器迭代所需的时间是关于各个地图中最大特征数量$\max_k N_t^{[k]}$的线性时间。后面我们会讨论具有更高效的先进数据结构。


算法 13.2.未知数据关联的FastSLAM 1.0算法。这个版本没有实现本章中所讨论的任何高效的树表达方式。	算法 13.3.未知数据关联的FastSLAM 2.0算法。

我们注意到这两种FastSLAM算法在一个时间只考虑了单一的测量值。和之前一样，这是为了符号上方便，并且可以应用很多之前SLAM章节中的技术。

13.8 高效实现

乍一眼看来，FastSLAM算法的每个更新都需要$O(MN)$的时间，其中$M$是粒子数量，$N$是地图中特征的数量。$M$的线性复杂度是不可避免地，因为在每个更新过程中都需要处理$M$个粒子。只要有一个粒子在不止一次的重采样过程中被选中，那么朴素的实现都可能复制一遍该粒子的地图。这个复制的过程需要地图尺寸$N$的线性时间。此外数据关联的朴素实现可能还要计算地图中$N$个特征的测量似然值，它们也都是$N$的线性复杂度。我们注意到一个糟糕的采样过程实现，可能很容易就附加了$\log N$的更新复杂度。

高效的FastSLAM算法的更新时间只需要$O(M\log N)$的时间。它是关于地图尺寸$N$的对数时间。首先考虑已知数据关联的情况，可以通过特定的记录粒子的数据结构来避免线性的拷贝开销。其基本思想就是用一个平衡二叉树balanced binary tree来组织地图。图13.8a中显式了这样的一棵针对单一粒子的树，描述了$M = 8$个特征。注意到所有的高斯参数$\mu_j^{[k]}$和$\Sigma_j^{[k]}$都在树的叶子上。假设树近似是平衡的，那么查找一个叶节点就需要$N$的对数时间。


(a)	(b)
图13.8. (a) 对于单一粒子的$N = 8$的特征估计树。(b) 从一个旧的粒子生成新的粒子，只修改一个高斯分布。新粒子只接收部分树，由修改的高斯路径构成。所有的其它指针都从生成树中拷贝得到。整个过程是$N$的对数时间完成的。

假设FastSLAM吸收了一个新的控制量$u_t$和一个新的测量值$z_t$。$Y_t$中的每个新粒子与$Y_{t-1}$中对应粒子，都有两个方面的不同。其一，它通过式($\ref{f26}$)获取一个不同的位姿估计。其二，按照式($\ref{f46}$)更新特征的高斯分布。所有其它高斯特征估计都相当于生成粒子。当拷贝粒子的时候，在表示所有高斯分布的树上，只有一个路径需要修改，这将导致对数的更新时间。

图13.8b中示例了这样的技巧。这里我们假设$c_t^i = 3$，因此只有高斯参数$\mu_3^{[k]}$和$\Sigma_3^{[k]}$需要更新。预期生成一棵新树，不如只创建一个到$c_t^i = 3$的新路径。这个路径是一个不完全树。通过拷贝生成粒子的树中缺少的指针补全树。因此，该路径的分支将指向生成树中未修改的相同的子树。显然，生成这棵树只需要$N$的对数时间。此外，访问一个高斯分布也只需要$N$的对数时间，因为索引到树中的一个叶节点需要路径长度个步骤。因此，生成和索引一个部分树可以在$O(\log N)$的时间内完成。因为每个更新过程中都有$M$个新粒子需要创建，所以整个更新过程需要$O(M\log N)$的时间。

以树的形式组织粒子存在一个问题，就是需要释放内存。内存释放基本可以以分期对数时间来实现。其思想就是为每一个节点赋予一个变量，包括树内部的节点和边缘上的叶子节点。该变量计数了指向对应节点的指针数量。每新创建一个节点其计数器就初始化为1。在创建其它粒子的时候产生了一个指向该节点的指针，就增加一个计数；当移除指针(比如说在重采样过程中所指的位姿粒子没有存活下来)就减少一个计数。当计数器为0的时候，其孩子节点的计数器递减，同时释放对应节点的内存。这个过程迭代的应用于计数为0的节点的所有孩子节点上，平均需要$O(M\log N)$的时间。

这个树还大量的减少了内存使用。图13.9中显示了实验测量的使用高效树计数的FastSLAM算法的内存消耗的结果。该图是一个实际的FastSLAM 1.0算法的运行结果，该算法使用$M = 100$的粒子构建基于特征的地图。该图说明对于一个有50,000个特征的地图中，改进后的算法可以节省两个数量级的内存。在更新时间上的节省与此类似。

图 13.9.FastSLAM 1.0的线性内存版本和$\log(N)$内存版本对比

要获得未知数据关联的对数时间复杂度的FastSLAM算法要更困难一些。具体的，我们需要一种技术约束数据关联搜索，让其查询一个特征的局部邻居，避免计算地图中所有$N$个特征的数据关联概率。此外，树还需要保持接近平衡。

实际上有很多中内核密度树kernel density trees, kd-trees的变型，它们可以满足这些假设，认定传感器测量的房产相比于地图的尺寸而言小很多。比如说，Procopiuc et al. (2003)提出的bkd-tree维护了一系列的更高复杂度的树。通过仔细地在这些树之间变换项，就可以获得在对数时间的复杂度，保证在分期对数时间里插入一个新特征到地图中。 Eliazar and Parr (2003)提出的DP-SLAM算法，使用历史树history trees，以一种类似这里所描述的方法，来高效的存储和索引。

13.9 基于特征地图的FastSLAM算法

13.9.1 经验告诉我们...

FastSLAM算法已经应用于很多地图表示方法和传感器数据上了。最基本的应用就是基于特征的地图，假设机器人装备有一个检测路标的距离和方向角的传感器。维多利亚广场数据集就是这样的一种数据集，我们已经在第十二章中讨论过。图13.10a中显示了通过对控制量积分得到的机器人路径。控制量是对机器人位置的一个比较差的估计器，运行了30分钟之后，机器人位置估计就与其GPS位置相差了超过100米。


(a)	(b)	(c)	(d)
图 13.10.(a) 里程计预测的机器人路径; (b)虚线是真实的路径，实现是FastSLAM 1.0的估计路径; (c) 在维多利亚公园上叠加了GPS路径(虚线)，平均FastSLAM 1.0路径(实现)。(d) 没有里程计信息创建的维多利亚公园地图。数据和航拍图像都是由澳大利亚户外机器人研究中心的José Guivant and Eduardo Nebot提供的

图13.10中剩余的三个图中显示了FastSLAM 1.0的输出。在所有的三个子图中，用虚线显示了GPS估计的路径，FastSLAM算法的输出则用实线表示。测量路径的RMS误差在4公里的路程中才偏差了4米。这个实验中粒子数量为$M = 100$。这个误差与其它目前最好的SLAM算法相比都是很出色的，比如说上一章中讨论的算法。FastSLAM算法的鲁棒性在图13.10d中有所体现，图中给出了无视运动信息的实验结果。实际上，基于里程计的运动模型由Brownian运动模型替代了。平均的FastSLAM误差很难与之前获得的误差区分开。

当将FastSLAM算法应用于基于特征的地图上时，考虑反面信息是很重要的。当反面信息用于估计每个特征的存在时，如13.6节所讨论的那样，很多虚假的特征就都可以从地图中移除了。图13.11中对比了考虑反面信息和未考虑的FastSLAM算法所构建的维多利亚公园地图。使用反面信息的算法在其地图中的特征数量少了44%。尽管正确的特征数量是不可知的，但是从图中可以看出很多虚假的特征都被移除了。


(a)	(b)
图 13.11.(a) 没有基于反面信息消除特征的FastSLAM结果。(b) 消除特征的结果

有必要对比一下FastSLAM和EKF SLAM算法，EKF SLAM算法是目前一个比较流行的benchmark算法。比如说，图13.12中对比了从1到5000不同粒子数量下的FastSLAM 1.0与EKF算法的准确性。为方便对比，EKF SLAM算法的误差在图13.12中用一条虚线表示。随着粒子数量的增加FastSLAM 1.0算法的准确度逐渐接近EKF的准确度，而且在接近10个粒子的时候就基本上没有很大差别了。这很有意思，因为10个粒子和100个特征的FastSLAM算法所需要的参数数量比EKF SLAM算法少一个量级，而精度基本在一个水平上。


图 13.12.FastSLAM 1.0与EKF算法在仿真数据上的准确度对比	图 13.13.FastSLAM 1.0与2.0在不同等级的测量噪声下的对比。FastSLAM 2.0一般都比1.0效果更好。这种差距在粒子数量较少的时候尤为明显。

在实际应用中，FastSLAM 2.0算法要比FastSLAM 1.0效果更好，只是这种改进只在特定的条件下才有意义。一般来说，当粒子数量$M$很大，并且测量噪声比运动不确定度更大的时候，这两种算法都能产生很好的结果。如图13.13所示，为使用$M=100$个粒子的两种FastSLAM算法的准确度关于测量噪声的函数。其中最重要的发现就是FastSLAM 1.0在低噪声仿真的时候效果相对较差。一种特使FastSLAM 1.0的实现是否具有这个毛病的方法就是，人为的在概率模型$p(z|x)$上放大测量噪声。如果放大之后，整个地图的误差下降了而不是上升，那么就是时候切换到FastSLAM 2.0了。

13.9.2 闭环

没有什么算法是完美的。存在一些问题，FastSLAM算法的效果比高斯方法要差。闭环loop closure就是这样的一个问题。在闭环问题中，机器人会通过未知地形而且有时会很长时间看不到一些特定的特征。在SLAM算法中维护关联特性是尤其重要的，在这样才可以在闭合环路的时候将信息传播到整个地图中。EKF和GraphSLAM算法直接维护了这种关联性，而FastSLAM算法通过其粒子集合的多样性来维护。因此闭环的能力依赖于粒子的数量$M$。样本集的多样性越好所得到的闭环效果就越好。因为，新的观测可以反过来影响到机器人过去的位姿估计。

不幸的是，通过剪去不重要的机器人路径，重采样最终将导致所有的FastSLAM粒子都共享着过去某点的历史。新的观测不能影响在该时间点之前观测到的特征位置。通过增加粒子的数量$M$这一历史时间点可以向后推迟。随着时间丢弃关联数据的过程使得FastSLAM算法能够高效的更新传感器数据。这个效率是要付出代价的，它将降低算法的收敛速度。抛弃关联信息意味着为了获得想要的准确度需要采集更多的数据。显然， FastSLAM 2.0相比于1.0，其改进的建议分布使得重采样消除的粒子数量减少了，但是它并没有解决这一问题。

实际上，多样性是很重要的，而且值得对实现做出优化来获得做大的多样性。图13.15中给出了闭环的粒子。图中显示了所有$M$个粒子的历史。在图13.15a中，FastSLAM 1.0的粒子在闭环的一段上有着相同的历史。新的观测不能够影响到这个阈值之前观测到的特征。在FastSLAM 2.0中，该算法可以维持多样性并扩展到环路的起始。这点对于可靠的闭环和快速收敛很重要。(译者按:其实我也不知道这段翻译的是个什么鬼)


(a)	(b)
图 13.15.给定粒子数量的情形下，FastSLAM 2.0可以闭合比1.0更大的环路。

图13.16a中给出了FastSLAM 1.0和2.0的闭环特性的实验对比。随着环路尺寸的增加，两个算法的误差都在增长。但是，FastSLAM 2.0一致比1.0的效果好。我们还可以从粒子的角度重新解释这一结果。闭合给定的环路，FastSLAM 2.0需要比1.0更少的粒子。


(a)	(b)
图 13.16.(a) 准确度关于闭环尺寸的函数，固定粒子的数量，FastSLAM 2.0可以闭合比1.0更大的环路。(b) FastSLAM 2.0与EKF算法的收敛速度对比。

图13.16b中显示了FastSLAM 2.0与EKF收敛速度的对比实验结果。在实验中在一个大型仿真环路中分别运行了具有1个、10个和100个粒子的FastSLAM 2.0算法和EKF算法10次。在每次运行时都使用不同的随机种子，产生不同的控制和观测量，来生成每个闭环。图中的RMS位置误差是对各个算法的10次运行结果的平均值。

随着机器人在环路中运动，误差会逐渐地在地图中建立起来。当机器人在150次迭代后形成了闭环，再次访问旧的特征就会对整个环路上地特征位置产生影响，降低了地图的总体误差。在EKF算法中这点是显然的。使用单一粒子的FastSLAM 2.0算法不能够影响到过去的特征，因此特征误差并没有下降。随着更多的粒子添加到FastSLAM 2.0中，滤波器就能够将观测应用到过去的特征位置上，使其收敛速度逐渐接近EKF。显然，如果环路的尺寸增加了，为了获得接近EKF的收敛时间，那么粒子的数量也需要响应增长。在FastSLAM表示中缺乏长距离关联是其相比于高斯SLAM技术最具争议的弱点。

13.10 基于栅格的FastSLAM

13.10.1 算法

在第9章中，我们研究了机器人环境的尺度表示方法占用栅格地图occupancy grid maps。这种表示的优点是它不需要任何关于路标的预定义。实际上，它可以对任何类型的环境建模。在本章的后续部分中，我们将扩展FastSLAM算法到这种表达形式下。

为了将FastSLAM算法应用于占用栅格地图中，我们需要三个在之前章节中定义的函数。其一，我们需要像式($\ref{f12}$)那样对运动后验$p(x_t | x_{t-1}^{[k]}, u_t)$采样。因此，我们需要这样一个采样技术。其二，我们需要一个估计每个粒子的地图的技术。这使得我们可以依赖于第九章中描述的占用栅格地图。其三，我们需要计算各个粒子的重要性权重。也就是，我们需要一种方法计算观测量$z_t$的似然值$p(z_t | x_t^k, m^{[k]})$，以位姿$x_t^k$和地图$m^{[k]}$以及最近的测量值$z_t$作为条件。

将FastSLAM扩展到占用栅格地图上的技术是比较直接的。算法13.4描述了占用栅格地图的FastSLAM算法。一点不令人惊讶，这个算法借鉴了部分蒙特卡洛定位和占用栅格地图。在该算法中所用的各个函数都是在定位和建图算法中的变型。

具体的，函数measurement_model_map$\left(z_t, x_t^{[k]}, m_{t-1}^{[k]}\right)$计算第$k$个粒子在给定位姿$x_t^{[k]}$，以及建立在之前测量值和该离子表示的路径上的地图$m_{t-1}^{[k]}$下的测量值$z_t$的似然度。此外还有，函数updated_occupancy_grid$\left(z_t, x_t^{[k]}, m_{t-1}^{[k]}\right)$计算新的占用栅格地图，给定第$k$个粒子的当前位姿$x_t^{[k]}$、关联地图$m_{t-1}^{[k]}$以及测量值$z_t$。

13.10.2 经验告诉我们...

图13.17中显示了一个典型的应用基于栅格地图的FastSLAM算法的例子。图中有三个粒子以及它们所对应的地图。每个地图都表示一个潜在的机器人的路径，它描述了为什么各个栅格地图看起来都不一样。中间的地图具有最好的全局一致性。

图 13.17.基于栅格地图的FastSLAM算法的应用。每个粒子都有自己的地图。并且其重要性因子是基于粒子自己的地图计算的测量值似然概率。

图13.19中描述了FastSLAM算法生成的一个典型的地图。这是一个28×28米的环境。机器人轨迹的长度是491米，平均速度0.19m/s。地图的分辨率是10厘米。为了学习这个地图，至少使用了500个粒子。在整个建图过程中机器人由两个循环。图13.18中显示了从纯粹的里程计数据计算的地图，可以看到机器人里程计的误差。


图 13.18.纯粹基于里程计，从激光雷达数据中生成占用栅格地图。图片由弗莱堡大学的Dirk Hähnel提供。	图 13.19.关联于具有最高累积重要性权重的粒子的占用栅格地图，该图是将算法13.4应用到图13.18中描述的数据得到的。本实验中的粒子的数量是500。而且本图中描述的路径都是由具有最大累积重要性权重的粒子描述的。

图13.20中的示例可以看到使用多个粒子的重要性，形象的描述了环路闭合前后的样本轨迹。如左图所示，机器人并不是很确定它相对于初始位置的具体位置。但是，一些重采样步骤之后，机器人就又进入了已知的地形中，足以显著的降低不确定度了如右图所示。


(a)	(b)
图 13.20.在图13.19中最外层环路封闭前(a)和封闭后(b)的所有样本轨迹。图片由弗莱堡大学的Dirk Hähnel提供。

13.11 总结

本章中展示了用于SLAM问题的粒子滤波器方法，称为FastSLAM算法。

FastSLAM的基本思想就是维护一个粒子集合。其中每个粒子都有一个采样的机器人路径。它还有一个地图，但是地图中的每个特征都有其自己的局部高斯分布来描述。这种表示方法需要地图大小的线性空间，以及粒子数量的线性空间。
之所以可以将地图表示成为各个高斯分布，而不是EKF SLAM算法中的那个大的联合高斯分布，是因为SLAM问题的因式分解结构。具体的，我们注意到地图特征在给定路径的情况下是条件独立的。通过对每个粒子的路径的分解，我们就可以简单的认为各个地图特征都是独立的，如此就可以避免像EKF那样维护它们之间的相互关系了。
FastSLAM的更新过程保持着传统的粒子滤波器的过程，采样新位姿，然后更新观测到的特征。这个更新可以在线完成，所以FastSLAM也是一种在线SLAM问题的解决方案。
我们注意到FastSLAM可以解决完全SLAM和在线SLAM两种问题。我们的推导过程认为FastSLAM是一种离线的技术，粒子表示对路径空间的采样，而不是对当前位姿空间的。但是，也证明了没有一个更新过程需要任何除了最近的位姿信息之外的其它任何知识。所以我们可以安全的抛弃过去的位姿估计。这使得FastSLAM算法可以像一个滤波器一样工作，而且避免了粒子的大小随时间线性的增长。
我们讨论了两种不同的FastSLAM实现，版本号为1.0和2.0。FastSLAM 2.0是一个改进版本的FastSLAM算法。它与基础版本的不同之处在于一个关键的思想，FastSLAM在采样新位姿的时候考虑了测量值。同时也引入了一些数学工具，但是FastSLAM 2.0被证明优于FastSLAM 1.0，需要更少的粒子。
使用粒子滤波器的思想，使得我们可以基于每个粒子建立数据关联变量。每个粒子可以建立在不同的数据关联上。这为FastSLAM提供了一个直接的强大的解决SLAM中数据关联问题的机制。之前的算法中，尤其是EKF和GraphSLAM，和SEIF，都要求整个滤波过程在一个时间点只做一个数据关联决策，因此在选择数据关联值的时候需要更仔细一些。
为了随时间高效的更新滤波器，我们讨论了使用树的形式记录地图的方法。这些表示方法可以将FastSLAM的更新复杂度从线性降到对数复杂度。这种树的思想在实际应用中很重要，因为它使得FastSLAM能够处理有$10^9$或者更多特征的地图。
我们还讨论了使用反面信息的技术。这种技术可以移除地图中没有足够证据支撑的特征。这里FastSLAM使用类似占用栅格地图一章中介绍的证据累积的方法。另一种方法维护了粒子的权重，当在一个粒子的地图中没有观测到一个特征，这个粒子就可以通过乘以一个对应的重要性权重来降低粒子的数值。
我们讨论了很多这两种FastSLAM算法的实际特性。实验表明这两种算法实际应用到基于特征的地图和尺度占用栅格地图中都表现得很好。从实际应用的角度看来，FastSLAM是目前可用的最好的概率学SLAM技术之一。它的尺度特性只有前两章中讨论的信息滤波器算法才能匹敌。
我们将FastSLAM 2.0扩展到不同的地图表示形式上。一种表示形式中，地图由激光雷达检测的点构成。这种情况下，我们能够抛弃通过高斯分布对特征的不确定度建模的思想，而是依赖于扫描匹配技术来实现FastSLAM 2.0中的前向采样过程。粒子滤波器的使用产生了鲁棒的闭环技术。

FastSLAM最大的限制可能是，它只是隐含地通过粒子的多样性来维护特征位置估计的关联性。在特定的环境中，与高斯SLAM技术对比起来，这对于算法的收敛速度有负面的影响。当使用FastSLAM技术时，就需要考虑降低粒子匮乏问题对结果的负面影响。

13.12 参考文献

通过组合参数化密度函数的样本计算变量集合的分布的思想是由Rao (1945) and Blackwell (1947)提出的。今天，这一思想已经成为了统计学中的一个常用工具(Gilks et al. 1996; Doucet et al. 2001)。第一个使用粒子滤波器解决环路封闭问题的建图算法可以在文献Thrun et al. (2000b)找到。Murphy (2000a); Murphy and Russell (2001)给出了将Rao-Blackwellized粒子滤波器用于SLAM领域中的形式化介绍，他们提出了在占用栅格地图背景中应用这一思想的技术。

FastSLAM算法最早是由Montemerlo et al. (2002a)开发的，他还开发了高效维护多个地图的树形表示方法。这个算法在高分辨率地图上的扩展形式归功于Eliazar and Parr，他们的算法DP-SLAM从激光雷达扫描数据中产生的地图具有空前的准确性和细节。它们的中心数据结构称作世谱树ancestry tree，它将FastSLAM树扩展到占用类型地图的更新问题上。一个更高效的版本称为DP-SLAM 2.0(Eliazar and Parr 2004)。FastSLAM 2.0算法由Montemerlo et al. (2003b)开发，它是建立在van der Merwe et al. (2001)的早期工作上。他们是在粒子滤波器理论的将测量值用作建议分布的一部分的先驱人物。本章中讨论的基于栅格的FastSLAM算法归功于Hähnel et al. (2003b)，他们将改进的建议分布思想与Rao-Blackwellized滤波器应用到了基于栅格的地图上了。Avots et al. (2002)描述了一种用于跟踪动态办公室环境中的门状态的Rao-Blackwellized滤波器。

FastSLAM算法的一个最重要的贡献在数据关联领域，所以在SLAM的数据关联领域中有很多文献。最早的SLAM工作(Smith et al. 1990; Moutarlier and Chatila 1989a)使用的是最大似然数据关联， Dissanayake et al. (2001)给出了详细的推导。这些数据关联技术的一个关键限制就是不能够增强互斥性mutual exclusivity，一个传感器测量看到了两个不同的特征不可能同时对应着世界中同一个物理特征。意识到这一点，Neira and Tardós开发了测试特征集合中关联性的技术，大大的降低了数据关联的错误数量。为了适应潜在关联的巨大数量，是特征数量的指数级，Neira et al. (2003)提出了在数据关联空间中随机采样的技术。然而，所有的这些技术都在SLAM后验概率中维护了单一的模式。Feder et al. (1999)在声纳数据上应用了贪心数据关联思想，但是实现了一个延迟决策来解决歧义。

在SLAM问题中维护多模态的后验概率的思想要追溯到Durrant-Whyte et al. (2001)，他们的算法sum of Gaussians使用混合高斯分布来表示后验概率。每个混合要素都跟踪着数据关联决策历史的一个不同的轨迹。FastSLAM继承了这一思想，但它使用的是粒子集合而不是高斯混合要素。懒散的数据关联思想要追溯到其它领域，比如说机器视觉中的流行的RANSAC算法(Fischler and Bolles 1981)。之前章节中表述的树算法要归功于Hähnel et al. (2003a)。正如之前提到的，他们与Kuipers et al. (2004)的工作是平行的。 Shatkay and Kaelbling (1997); Thrun et al. (1998b)描述了一个完全不同的数据关联算法，它使用期望最大化Expectation Maximization, EM算法解决关联度问题(see (Dempster et al. 1977))。 EM算法在数据关联阶段与地图构建阶段之间不断地循环迭代，实现了同时在地图参数空间和离散关联度空间地同时搜索。Araneda (2003)成功地将MCMC技术应用于离线SLAM的数据关联问题中。

数据关联问题自然会在多机器人地图融合问题中浮现。有很多论文开发了定位一个机器人相对于其它机器人的算法，它们建立在一个假设下，就是这些机器人工作在相同的环境下，而且它们的地图相互重叠(Gutmann and Konolige 2000; Thrun et al. 2000b)。Roy and Dudek (2001)开发了一种技术，机器人为了融合它们的信息必须碰面。对于一般的情况，一个数据关联技术必须考虑地图可能没有重叠的概率。Stewart et al. (2003)开发了一种粒子滤波算法，显式的对没有重叠的地图建模了。他们的算法包含了一个计算这些概率的贝叶斯估计器，考虑了环境中特定的局部地图有多普通common。在多机器人建图的数据关联问题中使用特征集合匹配的思想要归功于Dedeoglu and Sukhatme (2000)2000); see also Thrun and Liu (2003)。 Howard (2004)提出了一个新的非平面(non-planar)形式的地图，来规避不完全地图的不一致性。他的方法给出了非常准确的多机器人建图结果(Howard et al. 2004)。


(a)	(b)
图13.8. (a) 对于单一粒子的\(N = 8\)的特征估计树。(b) 从一个旧的粒子生成新的粒子，只修改一个高斯分布。新粒子只接收部分树，由修改的高斯路径构成。所有的其它指针都从生成树中拷贝得到。整个过程是\(N\)的对数时间完成的。